ВВЕДЕНИЕ
В процессе развития общества человеком устанавливаются закономерности процессов в различных явлениях и областях: физике, химии, биологии и многих других. Первичными в процессе познания являются результаты наблюдений, представляющие собой отправной пункт к построению модели явления или процесса.
Построение моделей по результатам наблюдений представляет собой формализацию, необходимую для определения основных признаков, связей и закономерностей, присущих объекту, и отсеивания второстепенных признаков. В качестве динамических объектов могут рассматриваться технические системы и процессы в них. Для одного и того же объекта в зависимости от конкретных требований практики и типа решаемой задачи может быть построен ряд моделей различной сложности.
В данной курсовой работе решается вопрос построения моделей на основе экспериментальных данных.
Цель работы – изучение метода планирования эксперимента при исследовании многофакторной динамической системы и его применения для получения линейной математической модели и проверки ее адекватности.
ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ
Вариант 4
6. Провести крутое восхождение
Составить план 23
Факторы Значения параметров оптимизации:
|
X1 |
X2 |
X3 |
|
6 |
40 |
0,22 |
|
10 |
80 |
0,40 |
|
14 |
120 |
0,58 |
|
Y1 |
Y2 |
Y3 |
Y4 |
|
0,12 |
0,1 |
1,1 |
0,12 |
|
0,06 |
0,06 |
0,06 |
0,08 |
|
0,2 |
0,18 |
0,18 |
0,2 |
|
0,18 |
0,16 |
0,16 |
0,16 |
|
0,14 |
0,12 |
0,12 |
0,16 |
|
0,11 |
0,12 |
0,12 |
0,1 |
|
0,24 |
0,23 |
0,23 |
0,21 |
|
0,20 |
0,22 |
0,22 |
0,18 |
ОСНОВНАЯ ЧАСТЬ
1. Построение матрицы планирования
Для этого сначала необходимо составить таблицу факторов и интервалов варьирования
Таблица факторов и интервалов варьирования
|
Факторы |
Уровни факторов |
Интервал варьирования J |
||
|
-1 |
0 |
+1 |
||
|
X1 |
6 |
10 |
14 |
4 |
|
X2 |
40 |
80 |
120 |
40 |
|
X3 |
0,22 |
0,40 |
0,58 |
0,18 |
Среднее значение рассчитывается по формуле:
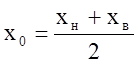
Определим интервал варьирования
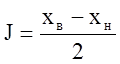
Составим матрицу планирования
|
№ |
Факторы |
Значение параметра оптимизации |
|||||
|
X1 |
X2 |
X3 |
Y1 |
Y2 |
Y3 |
Y4 |
|
|
1 |
- |
- |
- |
0,12 |
0,1 |
1,1 |
0,12 |
|
2 |
+ |
- |
- |
0,06 |
0,06 |
0,06 |
0,08 |
|
3 |
- |
+ |
- |
0,2 |
0,18 |
0,18 |
0,2 |
|
4 |
+ |
+ |
- |
0,18 |
0,16 |
0,16 |
0,16 |
|
5 |
- |
- |
+ |
0,14 |
0,12 |
0,12 |
0,16 |
|
6 |
+ |
- |
+ |
0,11 |
0,12 |
0,12 |
0,1 |
|
7 |
- |
+ |
+ |
0,24 |
0,23 |
0,23 |
0,21 |
|
8 |
+ |
+ |
+ |
0,20 |
0,22 |
0,22 |
0,18 |
2. Исключение ошибок экспериментов
В серии опытов 1 существует подозрение на ошибку. При одинаковых условиях получены следующие результаты:
Y = 0,12; 0,10; 1,1; 0,12.
Проверим эти значения на ошибку:
Для этого надо найти среднее значение и дисперсию для трех близких друг к другу значений.
Yср = 0,113
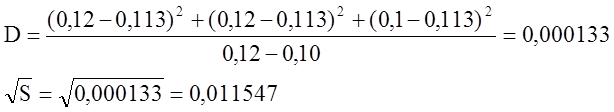
По критерию Стьюдента
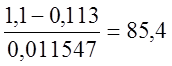 >3,18
>3,18
Следовательно, результат опыта 1,1 является ошибкой и его следует исключить из дальнейших расчетов.
Найдем среднее значение параметров оптимизации yср, дисперсию S2, а также число степеней свободы параметров оптимизации f.
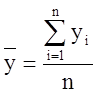
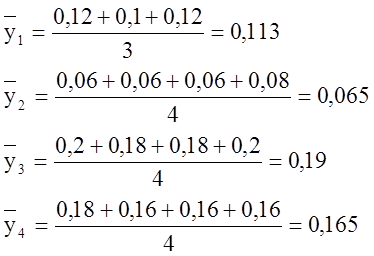
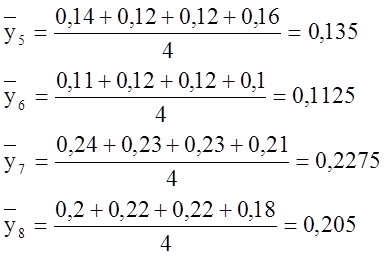
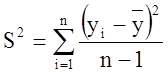
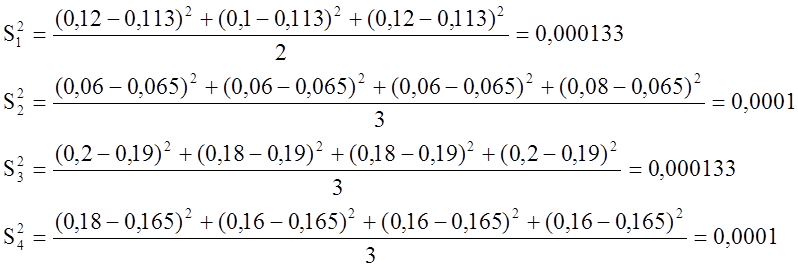
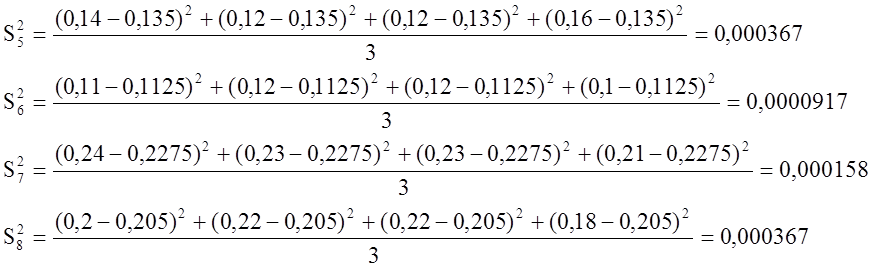
Занесем все значения в таблицу
|
№ |
Факторы |
Значение параметра оптимизации |
Среднее |
Дисперсия |
||||||
|
X1 |
X2 |
X3 |
Y1 |
Y2 |
Y3 |
Y4 |
Ycp |
f |
S2 |
|
|
1 |
- |
- |
- |
0,12 |
0,1 |
0,12 |
0,113 |
2 |
0,000133 |
|
|
2 |
+ |
- |
- |
0,06 |
0,06 |
0,06 |
0,08 |
0,065 |
3 |
0,0001 |
|
3 |
- |
+ |
- |
0,2 |
0,18 |
0,18 |
0,2 |
0,190 |
3 |
0,000133 |
|
4 |
+ |
+ |
- |
0,18 |
0,16 |
0,16 |
0,16 |
0,165 |
3 |
0,0001 |
|
5 |
- |
- |
+ |
0,14 |
0,12 |
0,12 |
0,16 |
0,135 |
3 |
0,000367 |
|
6 |
+ |
- |
+ |
0,11 |
0,12 |
0,12 |
0,1 |
0,1125 |
3 |
0,0000917 |
|
7 |
- |
+ |
+ |
0,24 |
0,23 |
0,23 |
0,21 |
0,2275 |
3 |
0,000158 |
|
8 |
+ |
+ |
+ |
0,2 |
0,22 |
0,22 |
0,18 |
0,205 |
3 |
0,000367 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.