Исследование динамической и статической модели гидросистемы, построение переходного процесса системы и определение показателей качества устойчивости системы

2 МОДЕЛИРОВАНИЕ НА МАКРОУРОВНЕ 2.1 Исходные данные

На рисунке 2 представлена схема моделируемой системы, в таблице 2 пара­метры гидромагистралей.

            Схема 8

Рисунок 5 - Принципиальная схема

Таблица 2 - Параметры гидросистемы

Наименование    параметра	Обозначение	Наименование магистрали
		1	2	3	4	5
Диаметр, м	dтр	20	30	32	32	15
Длина, м	l	1,5	2,5	1,9	1	0,9
Толщина стенки трубопровода, м	δтр		2,2
Коэффициент местных сопротивлений	ζ	4	5,5	5	5	3
Давление потребителя, Па	р	0,2/-	0,25/-	0,16/-	0,2/-	0,25,0,4/-

Рабочая жидкость - масло веретенное АУ: плотность р=860 кг/м³ ; вязкость ν=0,15*10^-4 м² /с; модуль упругости газожидкости смеси Е_с=1,7*10⁸ Па.

Материал трубопровода - латунь: модуль упругости Е_тр=9* 10¹⁰ Па.       Коэффициент потерь на трение при турбулентном потоке λ_т=0,028

2.2 Компонентные и топологические уравнения гидросистемы

Состояние сосредоточенных масс характеризуется фазовыми переменными типа потока, взаимодействия элементов отображаются фазовыми переменными типа потенциала. В гидравлической системе фазовые переменные типа потока -расход Q (м³/с), а типа потенциала - давление Р (Па).

Зависимость между двумя этими фазовыми переменными называется ком­понентным уравнением.

Топологические уравнения - уравнения равновесия, выражающие принцип Даламбера: геометрическая сумма всех сил, приложенных к телу, включая силу инерции, равна нулю.

1)  Условие равновесия потенциалов, действующих на сосредоточенные
массы: ∑ Р_i = 0;

2)  Условие непрерывности потоков жидкости: ∑Q_i = 0.

При построении динамической модели учтем основные свойства гидросис­темы, будем считать магистрали сравнительно короткими и рассматривать их дискретные элементы, наделенные инерционными и диссипативными свойст­вами. Магистрали рассматриваем как сосредоточенную массу. Т.к. длина со­единительной магистрали значительно меньше магистрали потребителей, то в 1-ом приближении массой жидкости можно пренебречь.

Вместе с насосами используются переливные клапаны, которые обеспечи­вают поддержание постоянного давления насосов Р_н = const. Внешнее воздейст­вие насоса и потребителей представляет собой источник типа потенциала. Ис­точники потенциалов описываются функциями давления.

Упругий элемент учитывает сжимаемость газожидкости и деформируе­мость стенок трубопровода, подключенного в точке ветвления гидромагистра­ли.

На рисунке 3 представлена схема динамической модели гидросистемы.

Рисунок 6 - Схема динамической модели гидросистемы.

При построении схемы динамической модели используются следующие обо­значения элементов гидросистемы.

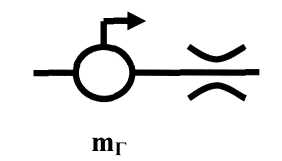1 Участок магистрали

2 Безынерционный участок магистрали

3 Насос с переливным клапаном и безымянным участком трубопровода

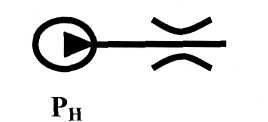
Модель содержит пять сосредоточенных масс m_Г1, m_Г2, m_Г3, m_Г4, m_Г5- Пять диссипативных элементов, обозначенных в виде постоянных дросселей с коэф­фициентом гидросопротивления μ_Г1, μ_Г2, μ_Г3, μ_Г4, μ_Г5, и один упругий элемент с коэффициентами гидрожесткости С_Г1 отображенных в виде гидроаккумулято­ров.

Внешнее воздействие на систему представлено в виде источников потен­циалов - давлений: Р_Н1 - источники, Р_В1, Р_В2, Р_В3, Р_В4 - потребители.

Фазовые переменные типа потока равны абсолютным расходам жидкости в выделенных участках магистрали типа потока Q₁, Q₂, Q₃, Q₄, Q_Н1.

2.3 Построение орграфа гидросистемы

Орграф (ориентированный граф - показано направление сигнала в ветвях графа) позволяет показать структуру и физические свойства моделируемой гидросистемы, и представляет собой ее ММ в графической форме.

Ветви графа и эквивалентной схемы соответствуют компонентам матема­тической модели. Они отображают математическое описание инерционных, упругих диссипативных элементов и источников внешних воздействий.

2.4 Составление матрицы инциденции

Информацию о ММ гидросистемы, которую содержит орграф представим в виде матрицы инциденции, сформированную по следующему правилу:

1. Размерность матрицы:

-  число строк, которые соответствуют каждому узлу орграфа за ис­-
ключением базы (1-6)

-  число столбцов, которые соответствуют ветвям орграфа (26)

2. Элементы матрицы:

-  отсутствие связи между узлом и ветвью = О

-  если ветвь входит в узел = 1

-    если ветвь выходит из узла =-1
Таблица 3 - Матрица инциденции

2.5. Использование узлового метода

Модификация узлового метода позволяет получить модель в виде системы ДУ в нормальной форме Коши, наиболее удобной для использования числен­ных методов интегрирования.

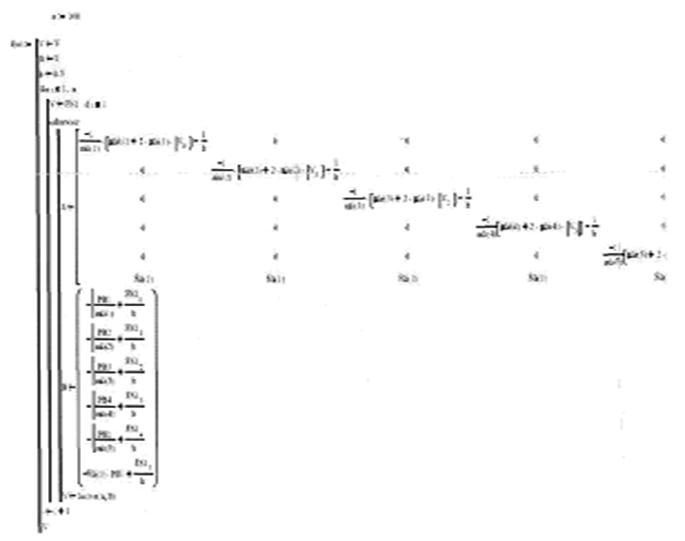
Согласно узловому методу записываем уравнение для гидродинамической системы:

На основании матриц инциденции выпишем следующие подматрицы:

Полученные выражения ММ по данному методу идентичны ММ, сформи­рованной по узловому методу.

2.7 Определение параметров элементов модели

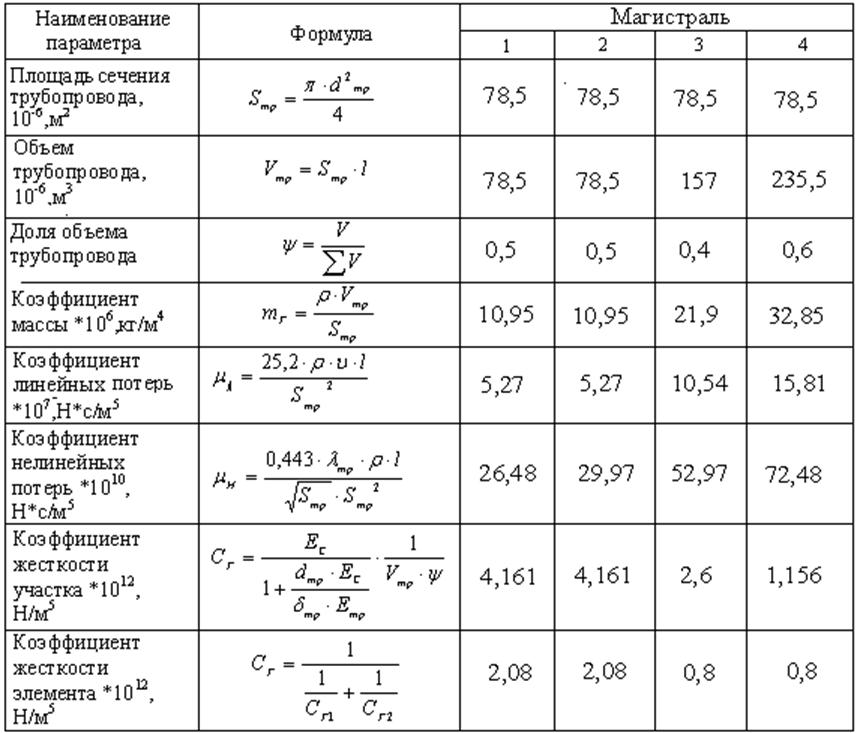
Расчет параметров гидросистемы приведен в таблице 4 Таблица 4 - Параметры гидросистемы

ЗАКЛЮЧЕНИЕ

В ходе выполнения курсовой работы было произведено моделирование на микроуровне и на макроуровне. Исследовали динамическую и статическую модель гидросистемы, построили переходный процесс системы и определили показатели качества устойчивости системы. Решили систему дифференциальных уравнений статической модели методом Ньютона, а динамическую модель рассчитали мето­дом Эйлера.

СПИСОК ЛИТЕРАТУРЫ

1.  Бутковский А.Г. Характеристики систем с распределенными параметрами.
-М.: Наука, 1979.-224с.

2.  Власов В.В. Синтез интегральной передаточной функции для объектов
управления с распределенными параметрами // Школа академика Власова:
Сб. метод, тр - М.: Буркин, 1998. -128с.

3.  Бесекерский В.А., Попов Н.П. Теория систем автоматического регулиро­
вания. М.: Наука. 1966. -992с.

4.  Топчеев Ю.И Атлас для проектирован ия систем автоматического регули­
рования. - М: Наука. 1989. -752с.

5.  Чемоданов Б.К., Иванов В.А., Медведев B.C., Юшенко А.С. Математиче­
ские основы теории автоматического регулирования. Том 1 - М: Высшая
школа, 1977. -366с.