Исследование систем с распределенными параметрами

Задание

Дифференциальное уравнение имеет вид:

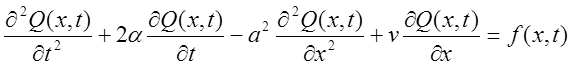
Начальные условия: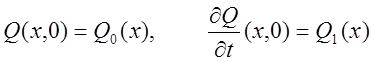

Граничные условия: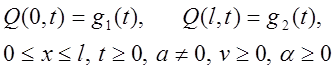

Нормирующая функция:

Континуальная передаточная функция:

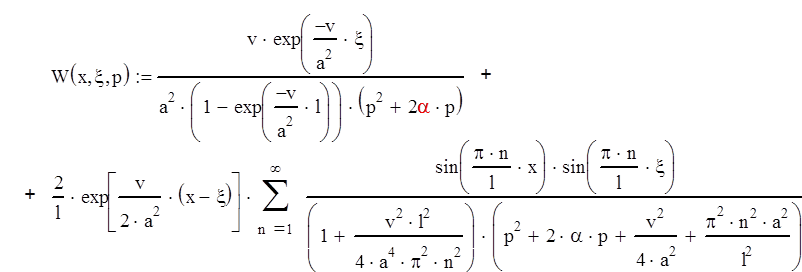По заданному дифференциальному уравнению объекта получить выражение для передаточной функции в распределенных параметрах, выражение для выходной величины, выражение для оценочной передаточной функции для наилучших условий управления. Построить оценочную ЛАЧХ, аппроксимировать ее с погрешностью 5%, записать выражение передаточной функции через типовые звенья.

По виду дифференциального уравнения определяем, что оно описывает сложные колебания. Зададим начальные, граничные условия и входное воздействие.

Нормирующая функция запишется в виде:

Изображение по Лапласу от нормирующей функции имеет вид:

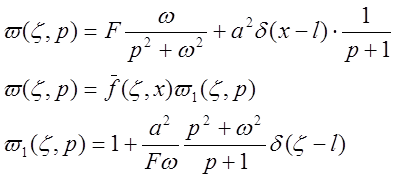
Изображение по Лапласу от вариации отклонения вычисляется по формуле:

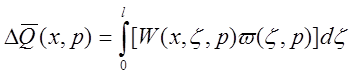
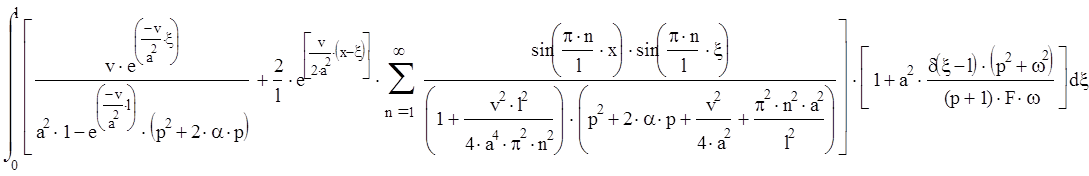
Вычислим интегральную передаточную функцию:

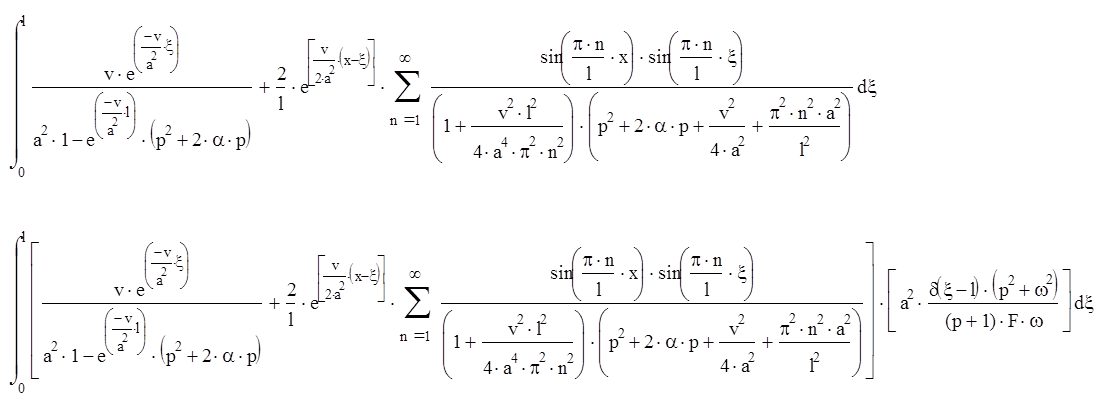
Для вычисления всего интеграла разобьем его на две части:

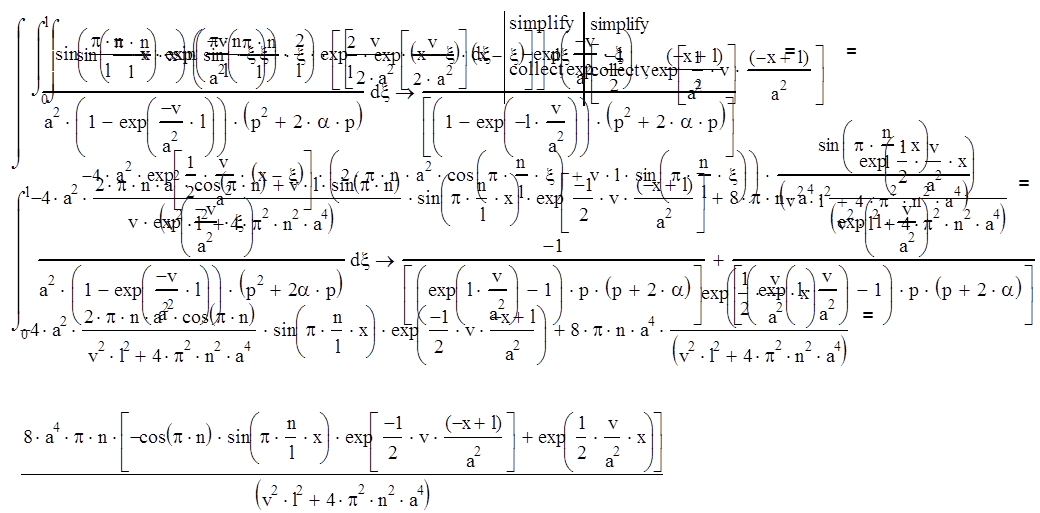
Вычислим интегралы некоторых слагаемых.

Подставим вычисленные интегралы в исходное выражение и сформируем интегральную передаточную функцию из двух промежуточных интегралов.

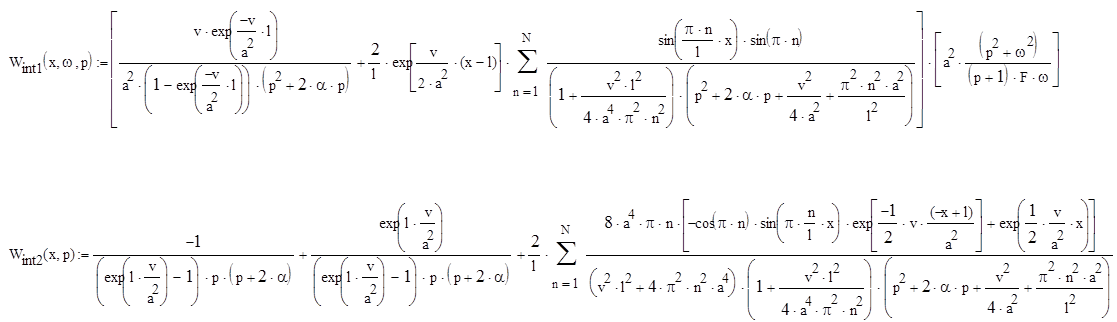
По полученной передаточной функции построим график ЛАЧХ, используя подстановки:

 

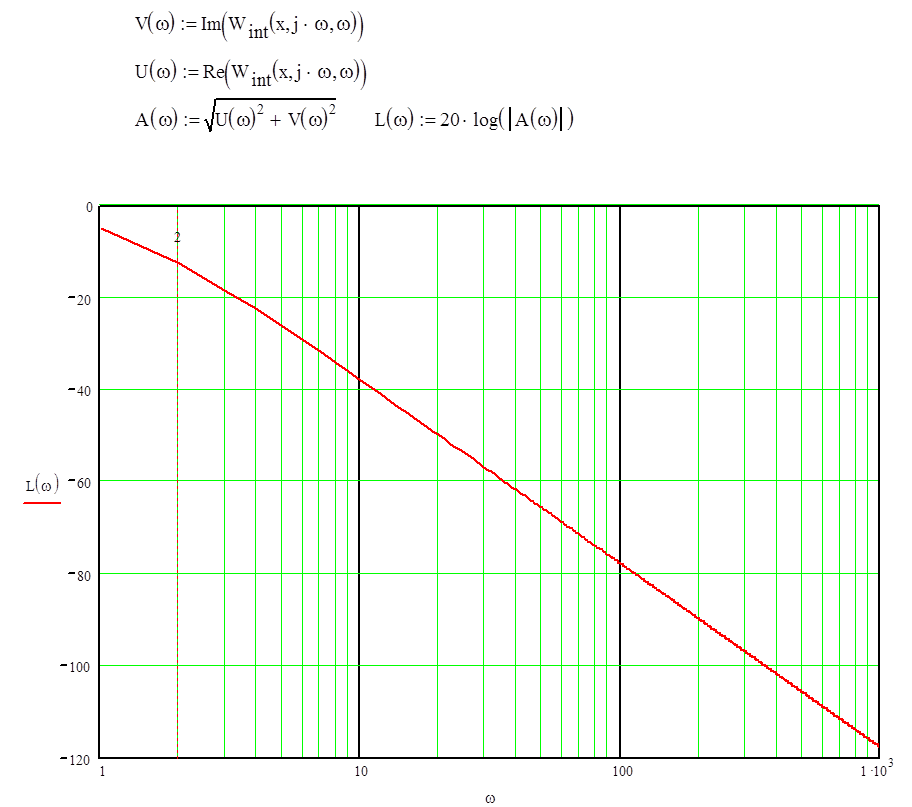
Из графика получим данные для записи передаточной функции.

w_и=2рад/с,  Т=1/w_и=0,5с, к₁=0,63.

Запишем передаточную функцию

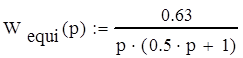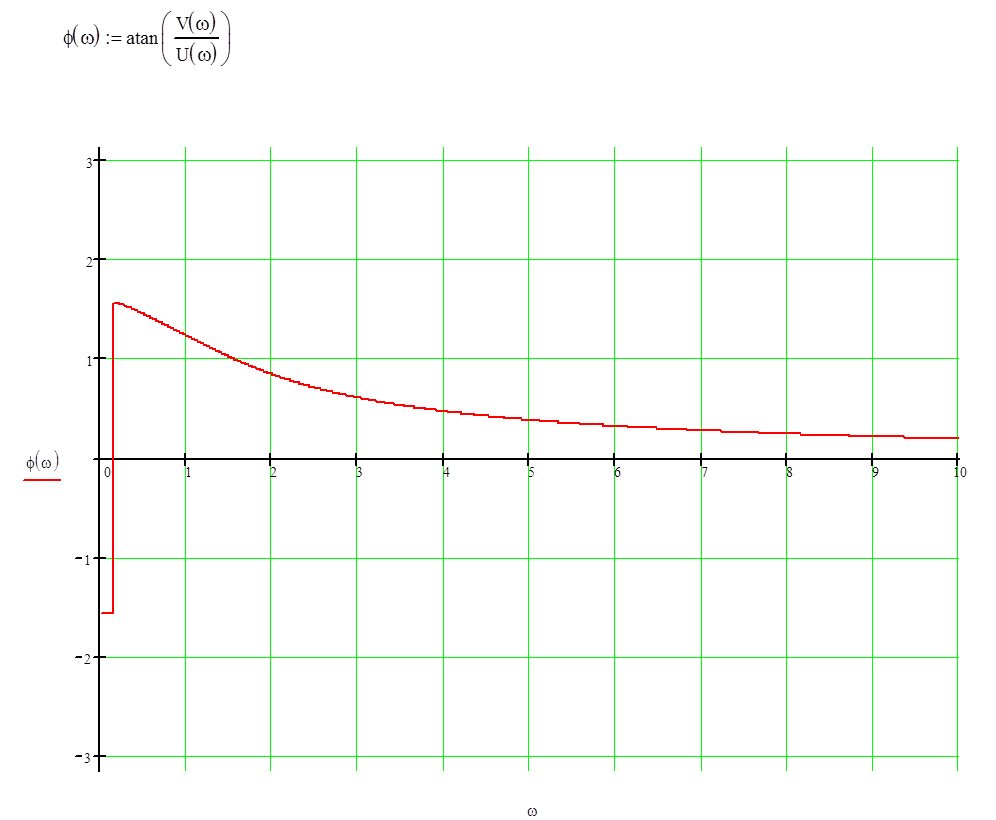
Построим график ФЧХ по интегральной передаточной функции

По виду полученной в результате аппроксимации передаточной функции определяем, что система состоит из пропорционального, интегрирующего и апериодического звена.

МИНИСТРЕРСТВО РОССИЙСКОЙ ФЕДЕРАЦИИ ПО ВЫСШЕМУ

И ПРОФЕССИОНАЛЬНОМУ ОБРАЗОВАНИЮ

БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ

ТЕХНОЛОГИИ И УПРАВЛЕНИЯ

КАФЕДРА УИТ

Курсовая работа

По курсу: «Моделирование систем управления»

Исследование систем с распределенными параметрами.

Выполнил: ст.гр. УИТ-41

Сергеев П.М.

Принял: препод.

Фролова М.А.

Балаково – 1999