Моделирование динамической системы методом планирования эксперимента. Вариант 1

Балаковский Институт Техники Технологии и Управления

Факультет: Инженерно-строительный

Специальность: УИТ

МОДЕЛИРОВАНИЕ ДИНАМИЧЕСКОЙ СИСТЕМЫ МЕТОДОМ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА

Вариант 1

Выполнил:

Студент гр. УИТ-41

Борисов В. В.

Проверил:

Преподаватель

Фролова М. А.

Балаково 2001

Задание: Составить план 2³.

Таблица 1

Уровни  факторов	Факторы процесса.
	Х1	Х2	Х3
Нижний	6	40	0.22
Основной	10	80	0.4
Верхний	14	120	0.58

Задан также массив данных:

Таблица 2

Y1	Y2	Y3	Y4
0.12	1.10	0.11	0.12
0.06	0.06	0.06	0.08
0.20	0.18	0.22	0.20
0.18	0.16	0.18	0.16
0.14	0.12	0.14	0.16
0.11	0.12	0.10	0.1
0.24	0.23	0.24	0.21
0.20	0.22	0.24	0.18

На основании заданных данных построим матрицу планирования.

Первоначально введем условное обозначение верхнего(+) и нижнего(-) уровня. Также в таблицу включим столбцы для среднего значения параметров оптимизации, дисперсии, для коэффициентов линейной модели и  степеней свободы для каждой серии опытов.

  Таблица 3

№ опыта	Х1	Х2	Х3	yср.	S2	Dy2	fi=n-1
1	-	-	-	0.1167	0.000033	0.00009216	2
2	+	-	-	0.065	0.0001	0.00007225	3
3	-	+	-	0.2	0.000267	0.00000529	3
4	+	+	-	0.17	0.000133	0.00000169	3

5	-	-	+	0.14	0.000267	0.00000121	3
6	+	-	+	0.1075	0.000092	0	3
7	-	+	+	0.23	0.0002	0.00003969	3
8	+	+	+	0.21	0.000667	0.00005329	3

 Среднее арифметическое результатов:

у_ср = (y₁ + y₂ + y₃ + . . . + y_n) / n =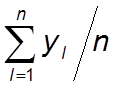                    

где у_l - результаты экспериментов, n - количество опытов в серии.

Подсчитаем дисперсию различных серий опытов.

                              S²=S(y_i-y_ср)²/(n-1)

Проверяем первую серию опытов на наличие ошибки:

Так как дисперсия S²=0.000033, то

                               (y-y_ср)/S²=29550>t=4.3

где t- коэффициент Стьюдента для степеней свободы (n-1)=2

А значит значение опыта равное 1.10-промах и из дальнейшего рассмотрения мы его исключаем.

Проверяем дисперсию на однородность:

                               S²_max/S²_min=0.000667/0.000033=20

Полученное значение меньше табличного значения критерия Фишера равного F=164.4

Находим дисперсию выходного параметра (дисперсия параметра оптимизации) вычисляется:

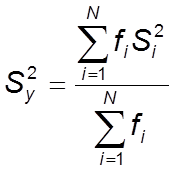                             = 0.000228

Рассчитаем коэффициенты для линейной модели:

                               b_i=Sx_iy_i/N           

Коэффициент b₀  есть среднее арифметическое значений параметра оптимизации

Получили линейную модель:

                               y=0.1549-0.016775x₁+0.0476x₂+0.016975x₃

Найдем квадрат отклонения расчетного значения от экспериментального:

                               Dy²=(y_ср.-y)²

Затем находим дисперсию адекватности для равномерного дублирования:

                              S²_ад=SDy²_i/f₂=0.000066395

Где f₂=N- (k+1)=4 , где к - кол-во уровней факторов.

Проверим модель на адекватность для чего находим расчетный коэффициент Фишера:

                               F_расч=S²_ад/S²_y=0.3017954

Полученное значение сравниваем с табличным значением критерия Фишера F=5.8 для степеней свободы числителя f₂=4 и знаменателя f₁=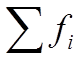=23 и поскольку полученное значение не превышает его, то полученная модель адекватна.

Оценим значимость коэффициентов для чего найдем дисперсию коэффициентов регрессии:

                               S²_b=S²_y/N=0.0000285

На основе полученной дисперсии коэффициентов регрессии строим доверительный интервал по формуле:

                              Db=± tS_b=0.016976554 ,где t=3,18

Получили, что коэффициенты b₁ и b₄ больше доверительного интервала.

Получили линейную модель в виде: y=0.1549+0.0476x₂

Таблица 4

Коэффициенты	b2=0.0476
Jibi	1.904
Шаг	7.616
	x2
Опыт                  1	87.616
2	95.23
3	102.848
4	110.464
5	118.08
6	Опыт не рассматриваем

Так как в модели используются кодированные значения факторов, а в таблице натуральные значения, то переходим по формуле:

                               X_i=(x_i-x_i0)/J_i

где  X_i - кодированное значение фактора, x _j  - натуральное значение фактора, x _j0  - натуральное значение основного уровня, J _j  - интервал варьирования, j - номер фактора.

Таблица 5

Опыт	Х2	Y
1	0.1904	0.163963
2	0.3808	0.173026
3	0.5712	0.182089
4	0.7616	0.191152
5	0.952	0.200215

Ответ: наибольшее значение параметра оптимизации равно 0.23 при значениях факторов Х1=6, Х2=120, Х3=0.58.