Изучение метода планирования эксперимента при исследовании многофакторной динамической системы и его применения для получения линейной математической модели и проверки ее адекватности, страница 2

Проверка на однородность:

Наибольшая и наименьшая дисперсия выделены в таблице. Этим значения соответствует число степеней свободы = 3. Значение критерия Фишера при этих условиях равно 9,3.

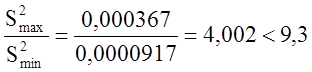
Дисперсия однородна, т.к. расчетное значение меньше значения критерия Фишера.

3. Построение линейной модели

где b₀ – среднее арифметическое из Y_ср; b₁ - среднее арифметическое из Y_ср (со знаками 1-го столбца); b₂ - среднее арифметическое из Y_ср (со знаками 2-го столбца); b₃ - среднее арифметическое из Y_ср (со знаками 3-го столбца).

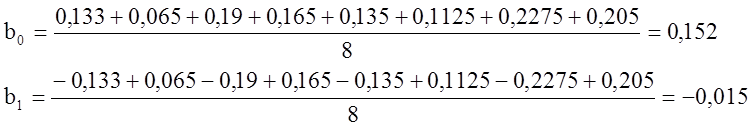
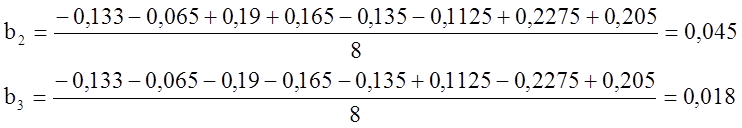
4. Проверка на адекватность

Считаем дисперсию адекватности

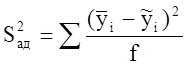
 - значение параметра оптимизации полученное расчетным путем

f = N – (K + 1);

где  N – количество серий опытов; К – количество факторов.

f = 8 – (3 + 1) = 4

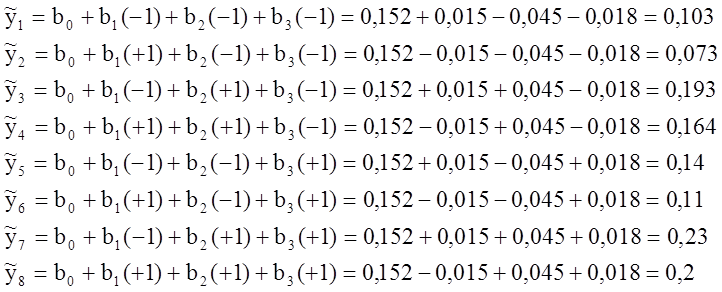
Таким образом дисперсия адекватности будет равна:

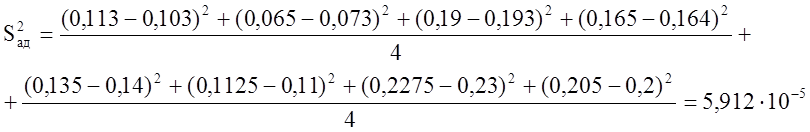
Найдем дисперсию параметра оптимизации

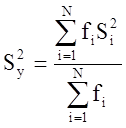, где f_i – число степеней свободы в i-м опыте.

 

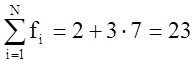
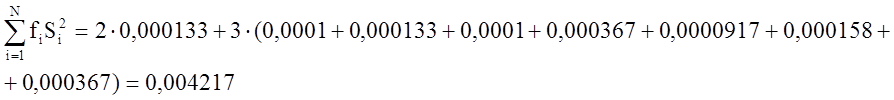
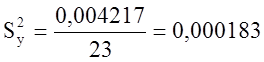
Для проверки адекватности модели используется Ф-критерий Фишера, который определяется следующей формулой:

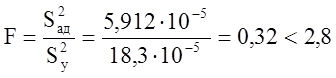
Дисперсия адекватна, т.к. расчетное значение меньше табличного.

5. Оценка коэффициентов модели

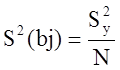
, где t – значение критерия Стьюдента (при степени свободы для S_y²)

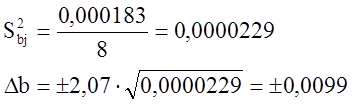
Проверка показала, что все коэффициенты (b₀ = 0,152; b₁ = -0,015; b₂ = 0,045; b₃ = 0,018) являются значимыми и их абсолютная величина больше доверительного интервала Db.

6. Крутое восхождение

Факторы	Х1	Х2	Х3
Нижний	6	40	0,22
Средний	8	80	0,40
Верхний	10	120	0,58
Интервал варьирования	2	40	0,18
b	-0,015	0,045	0,018
Jb	-0,03	1,8	0,00324
Шаг	-0,06	3,6	0,00648
Опыты
1	7,94	83,6	0,40648
2	7,88	87,2	0,41296
3	7,82	90,8	0,41944
4	7,76	94,4	0,42592
5	7,7	98	0,4324
6	7,64	101,6	0,43888
7	7,58	105,2	0,44536
8	7,52	108,8	0,45184
9	7,46	112,4	0,45832
10	7,4	116	0,4648
Опыты	X1	X2	X3
1	-0,03	0,09	0,036
2	-0,06	0,18	0,072
3	-0,09	0,27	0,108
4	-0,12	0,36	0,144
5	-0,15	0,45	0,18
6	-0,18	0,54	0,216
7	-0,21	0,63	0,252
8	-0,24	0,72	0,288
9	-0,27	0,81	0,324
10	-0,3	0,9	0,36

Для принятия решения после построения модели рекомендуется движение по градиенту. Составляющие градиента однозначно получаются умножением коэффициентов регрессии на интервал варьирования по каждому фактору. Серия опытов в направлении градиента рассчитывается последовательным прибавлением к основному уровню факторов величин, пропорциональных составляющим градиента.

Опыты	X1	X2	X3	Y
1	-0,03	0,09	0,036	0,157
2	-0,06	0,18	0,072	0,162
3	-0,09	0,27	0,108	0,167
4	-0,12	0,36	0,144	0,173
5	-0,15	0,45	0,18	0,178
6	-0,18	0,54	0,216	0,183
7	-0,21	0,63	0,252	0,188
8	-0,24	0,72	0,288	0,193
9	-0,27	0,81	0,324	0,198
10	-0,3	0,9	0,36	0,203

ЗАКЛЮЧЕНИЕ

Движение по градиенту не привело к улучшению параметра оптимизации по сравнению с лучшим результатом в матрице планирования эксперимента. Таким образом, наилучший опыт – опыт №7 в матрице планирования, при котором значение параметра оптимизации равно 0,24. Факторы процесса при этом опыте оказались следующими:
x₁ = 6; x₂  =120; x₃ = 0,58.

СПИСОК ЛИТЕРАТУРЫ

1.  Дейч А.М. методы идентификации динамических объектов. – М.: Энергия, 1979. – 240 с.

2.  Спиридонов А.А. Планирование эксперимента при исследовании технологических процессов. – М.: Машиностроение, 1981. – 184 с.

3.  РДМУ 109-77. Методические указания: методика выбора и оптимизации контролируемых параметров технологических процессов. – М.: Изд-во стандартов, 1978. – 64 с.

4.  Адлер Ю.П., Александрова И.Ф. Грановский Ю.В. Об  одном методе формализации априорной информации при планировании эксперимента. – М.: Наука, 1966. – 70 с.