Задания на лабораторную работу 1,2, вариант 11 (Решить уравнение. Найти корни полинома. Решить систему уравнений двумя способами. Найти точки min и max функции y=f(x). Преобразовать нелинейные уравнения системы)

Вариант №11

Задание №1   Решить уравнение:

          

        

           

          

                    

          

Задание №2   Найти корни полинома.

               

        

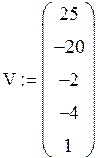
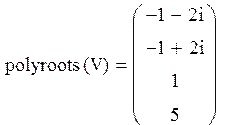
Задание №3    Решить систему уравнений двумя способами: методом  и с           помощью функции lsolve.

                 

                                                            

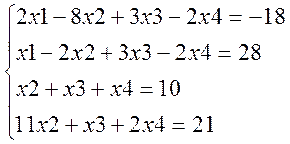
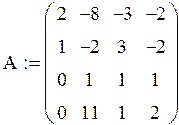
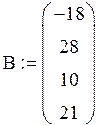
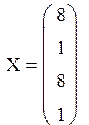
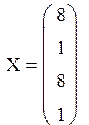
        Задание №4   Найти точки min и max функции y=f(x)

          

       

       

          

       

       

        Задание№5   Преобразовать нелинейные уравнения системы к виду  и    f2(y)=x..Построить их графики и определить начальное приближение решения. Решить систему нелинейных уравнений, используя функцию Minerr.

        

        

                             

                               

        

        

                 

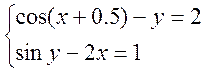
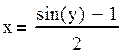
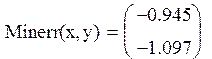
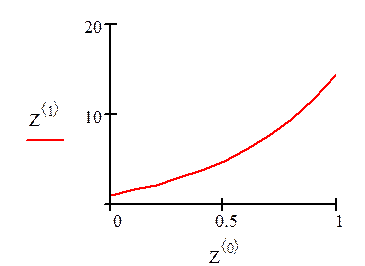
    Задание №6    Решить задачу Коши: 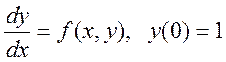 с шагом h=0,1 на отрезке [0.1] используя функцию rkfixed.

                   

                       

     Задание №7    Найти аналитическое решение ОДУ из задания 6 с помощью преобразований Лапласа

        

           

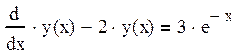
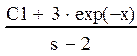
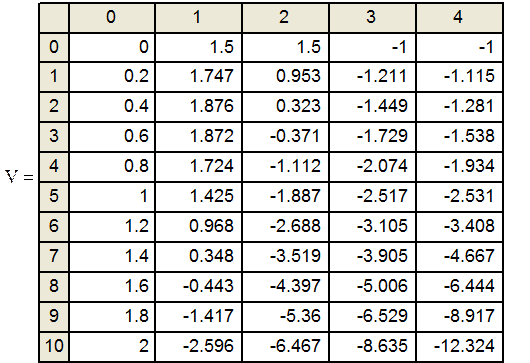
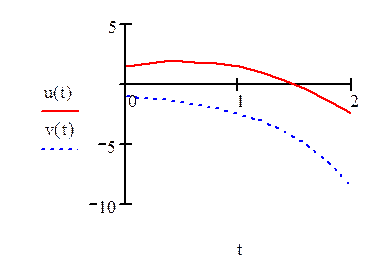
    Задание №8     Решить задачу Коши для системы ОДУ при заданных начальных условиях на отрезке [0,2] с шагом h=0,2.Решать с помощью функции rkfixed. Построить графики функций u(t) и v(t).

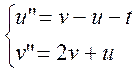    Начальные условия:     u(0)=1.5,  u’(o)=1.5, v(0)=-1,  v’(0)=-1

           

               

                  

                                                       

           

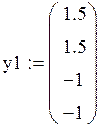
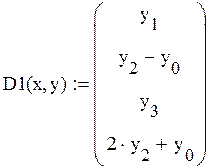
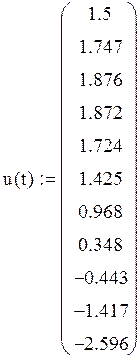
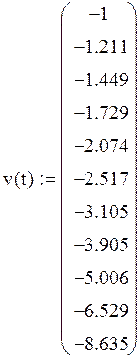
Задание №9    На отрезке [a,b] с использованием функций load, score и sbval преобразовать краевую задачу: 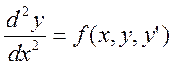 при граничных условиях y(a)=A, y(b)=B к задаче Коши и найти решение заданного ОДУ в 10 промежуточных точках с помощью функции rkfixed.

f(x, y, y’)=

    Граничные условия: a=-3,   b=-2,   y(a)=3,   y(b)=0

               

       

       

 

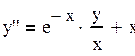
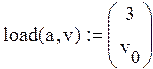
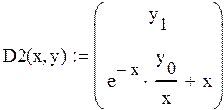
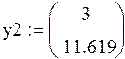
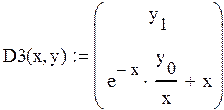
                 x           y(x)       y`(x)

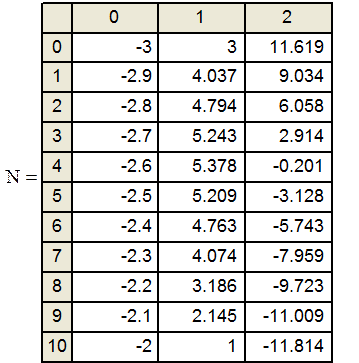
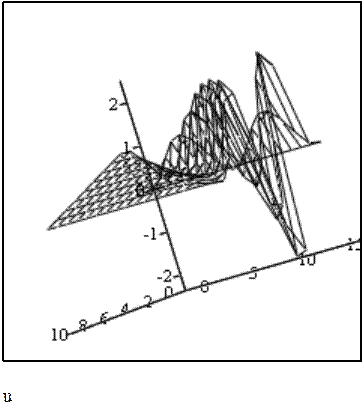
       Задание №10 Решить задачу о колебании струны единичной длины с  закрепленными краями.

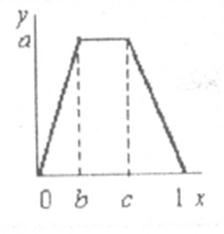               a=1,   b=0.1,  c=0.2              

                        

 

             

  

  

   

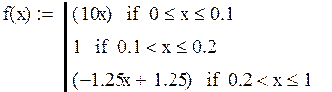
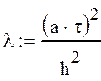
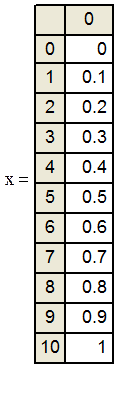
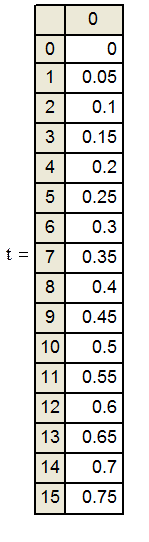
Начальные и граничные условия для решения волнового уравнения:

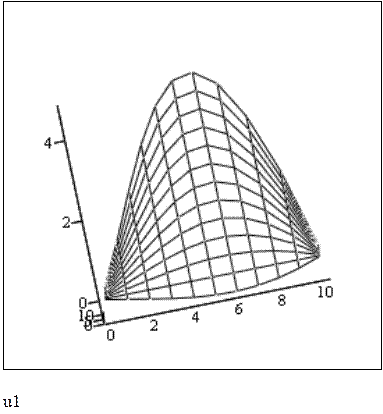
Задание №11   Найти решение u(x,t) для уравнения теплопроводности с постоянными коэффициентами.

Начальные и граничные условия для решения уравнения теплопроводности:

   

Задание №12  Найти стационарное распределение температуры в квадратной пластине со стороной 1, описываемое уравнением Лапласа

                                           

                         

                   

               

                                                                                                           

     

                   

           

  

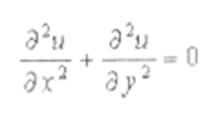
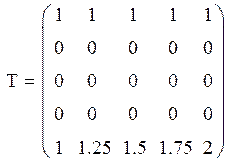
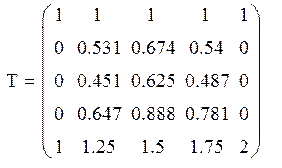
  Задание №13   Выполним операции с помощью команд символьного процессора.