Упрощение структурных схем и проверка системы на устойчивость

Практическая работа №1.

Упрощение структурных схем и проверка системы на устойчивость.

Задание:

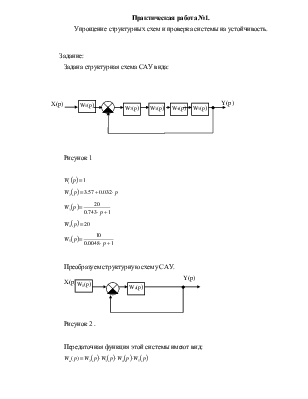
Задана структурная схема САУ вида:

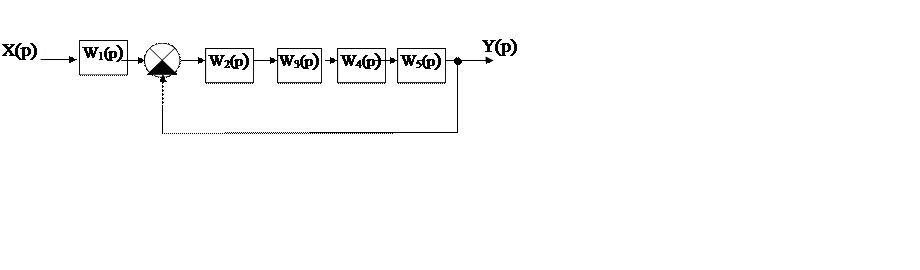
Рисунок 1

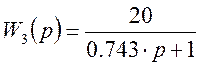
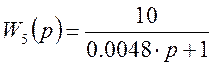
Преобразуем структурную схему САУ.

Рисунок 2 .

Передаточная функция этой системы имеют вид:

Теперь заменим встречно-параллельное соединение, одним звеном и учтем это соединение  с звеном W₁(p).

Тогда:

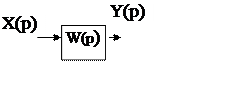
Рисунок 3.

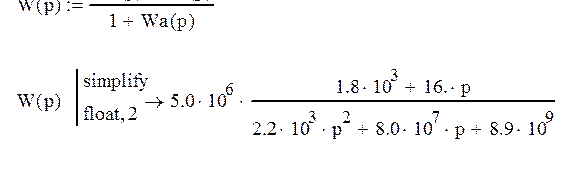
Мы получили передаточную функцию замкнутой системы.

Получим передаточную функцию разомкнутой системы:

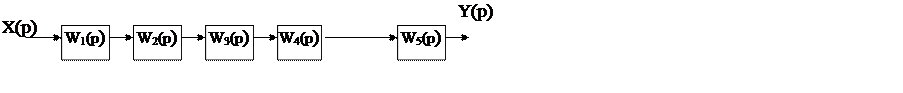
Рисунок 4.

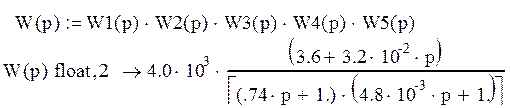
1.  Критерий устойчивости  Рауса.

Дня того, чтобы САУ была устойчива необходимо и достаточно, чтобы все коэффициенты первого столбца таблицы Рауса имели один и тот же знак, а при а₀>0 были бы положительными.

Из передаточной функции характеристическое уравнение для замкнутого состояния САУ имеет вид

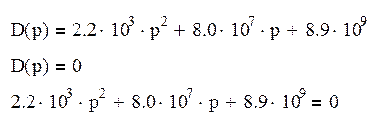
Таблица Рауса составляется из коэффициентов характеристического уравнения, которые располагаются в таблице по строкам и столбцам. В 1 строке записываются коэффициенты с четными индексами, а во второй – с нечетными. Все остальные клетки таблицы заполняются коэффициентами, которые вычисляются так:

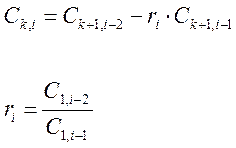
k – номер столбца в таблице, i – номер строки.

Составим таблицу Рауса для нашей системы.

Таблица 1.

	Номер строки – i.	Номер столбца – k.
		k=1	k=2
-	1
-	2
	3
	4

Из таблицы видно, что все коэффициенты положительны, значит САУ – устойчива.

2.  Критерий устойчивости Гурвица.

Для того, чтобы САУ была устойчива необходимо и достаточно, чтобы все определители Гурвица были положительны.

составим определители Гурвица и вычислим их

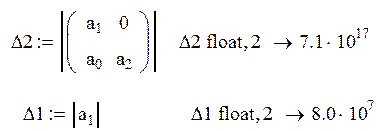
Так все определители положительны при положительном а₀, то САУ является устойчивой.

3.  Критерий устойчивости   Льенера-Шипара.

Для того, чтобы САУ была устойчива необходимо и достаточно, чтобы были положительны все коэффициенты характеристического уравнения для замкнутого состояния и главные миноры нечётного порядка определителя Гурвица.

Характеристическое уравнение для замкнутого состояния САУ  является уравнением 2 порядка.

Для уравнения 2 порядка условия устойчивости имеют вид

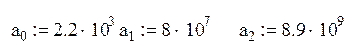
Все условия выполняются, САУ устойчива.

4.  Критерий устойчивости Ляпунова.

Для того чтобы САУ была устойчива необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательные вещественные части.

Определим корни характеристического уравнения.

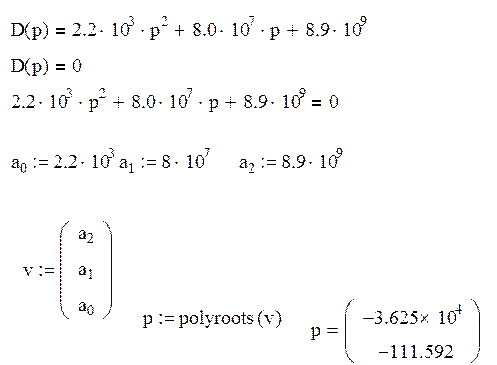
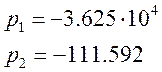
Так как  все корни характеристического уравнения имеют отрицательную вещественную часть, то САУ будет устойчивой.

5.  Критерий устойчивости Михайлова.

Для того, чтобы САУ была устойчива необходимо и достаточно, чтобы кривая Михайлова, начинаясь на положительной полуоси проходила последовательно n квадрантов в направлении против часовой стрелки, где n -порядок характеристического уравнения.

В характеристическом уравнении заменим

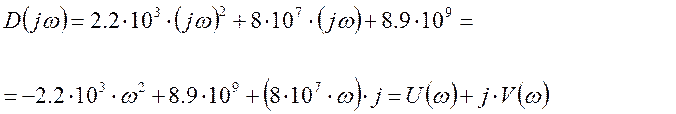
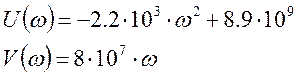
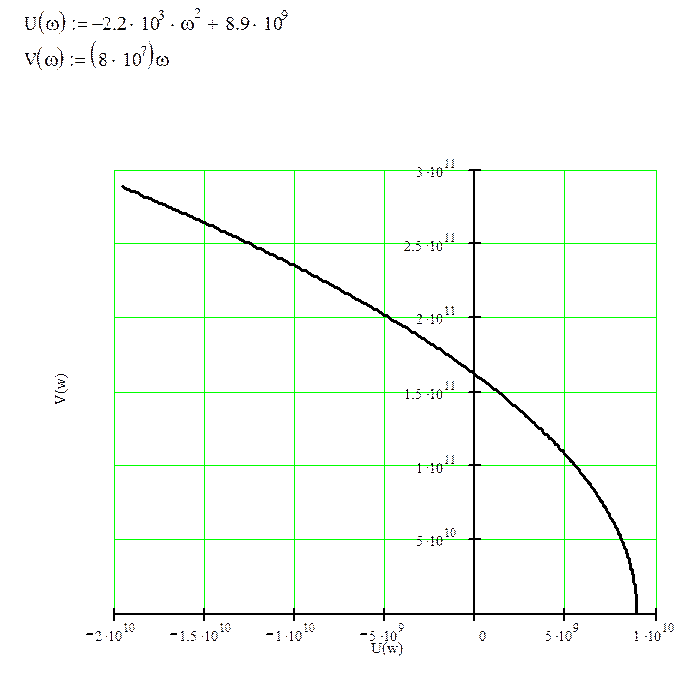
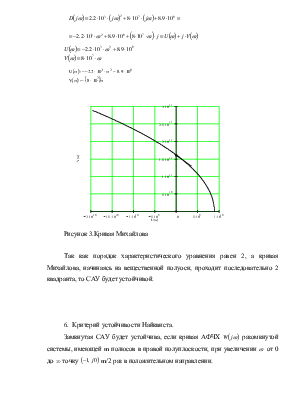
Рисунок 3.Кривая Михайлова

Так как порядок характеристического уравнения равен 2, а кривая Михайлова, начинаясь на вещественной полуоси, проходит последовательно 2 квадранта, то САУ будет устойчивой.

6.  Критерий устойчивости Найквиста.

Замкнутая САУ будет устойчива, если кривая АФЧХ  разомкнутой системы, имеющей m полюсов в правой полуплоскости, при увеличении  от 0 до  точку  m/2 раз в положительном направлении.

где U(ω)- действительная составляющая, V(ω)- мнимая составляющая.

В выражении для передаточной функции разомкнутой системы заменим  и выделим действительную и мнимую составляющие.

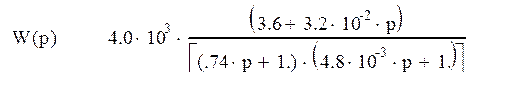
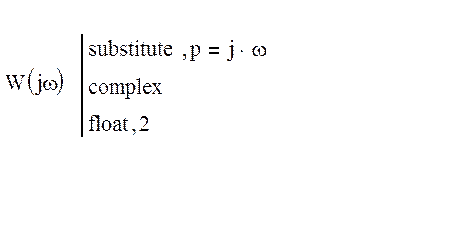
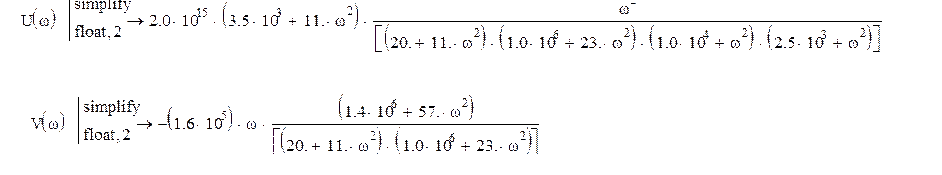
Для определения знака полюсов m найдём корни характеристического уравнения разомкнутой системы.

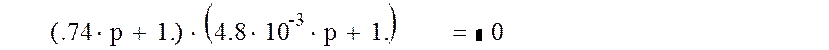
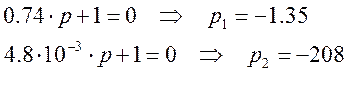
То есть все корни расположены в левой полуплоскости и тогда m=0.

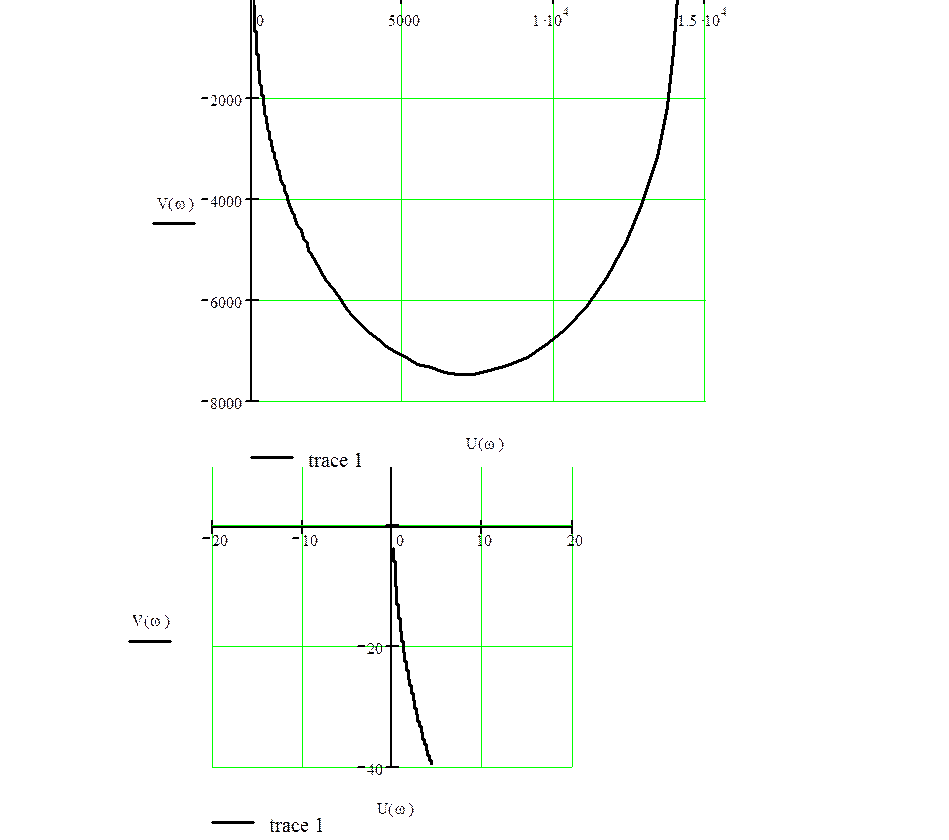
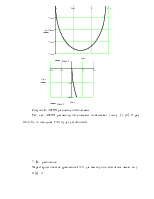
Рисунок 6.-АФЧХ разомкнутой системы.

Так как АФЧХ разомкнутой системы охватывает точку  0 раз (m/2=0), то исходная САУ будет устойчивой.

7.  D – разбиение.

Характеристическое уравнение САУ для замкнутого состояния имеет вид:

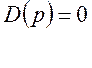
Уравнению соответствует следующая форма записи

Выразим из него коэффициент а₂

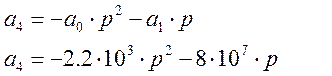
В последнем выражении заменим р на jw и выразим действительную и мнимую части.

 

Задаваясь -, построим кривую D-разбиения по одному параметру а4

D(0)

D(1)

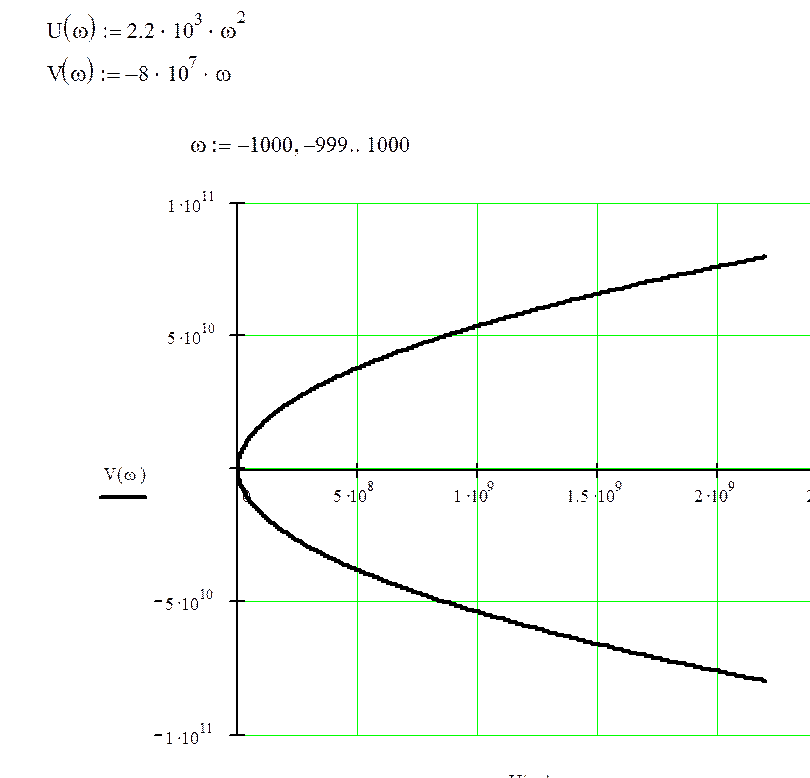
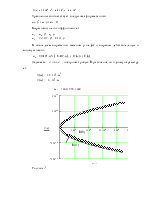
Рисунок 7.

Так как а₂ входит в область  D(0), то проверим эту область на устойчивость. Пусть a₄=10⁹, тогда характеристическое уравнение примет вид:

Решая это уравнение, получаем, что:

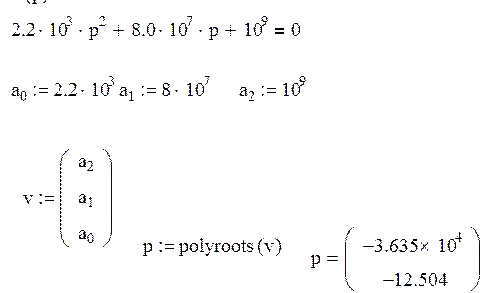
так как все корни имеют отрицательную вещественную часть, то по Ляпунову САУ будет неустойчивой, а это значит, что область D(0), является областью устойчивости системы по параметру a₂.

8.  Критерий устойчивости Шур - Кона.

Для того, чтобы САУ была устойчива, необходимо и достаточно, чтобы определители Шур - Кона с нечетными индексами были меньше 0, а – с четными индексами были больше 0.

В  этом случае корни характеристического уравнения для замкнутого состояния, записанного в форме z-преобразования, будут лежать внутри единичной окружности.

Передаточная функция уравнение для  замкнутого  состояния   САУ  имеет вид:

Упростим выражение:

Запишем вышеприведенное выражение в виде z-преобразований.

Определитель Шур - Кона имеет вид:

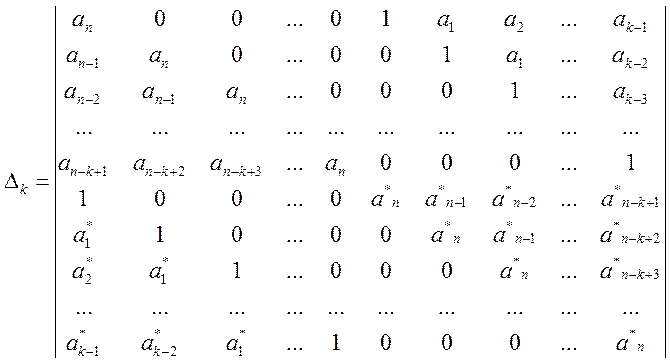
Составим и вычислим четные и нечетные определители Шур-Кона.

Все условия устойчивости выполняются (Δ1<0, Δ2>0), значит САУ – устойчива.