







САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
БАЛАКОВСКИЙ ИНСТИТУТ, ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ
КАФЕДРА: «УИТ»
УЗЛОВОЙ МЕТОД ФОРМИРОВАНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
Методические указания к практической работе по дисциплине
«Моделирование систем» специальности 210100
Одобрено
редакционно-издательским советом Балаковского института техники,
технологии и управления
2005
Цель работы: овладение навыками построения динамической модели технической системы с использованием узлового метода на основании заданной матрицы инциденций
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
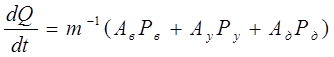 (1)
(1)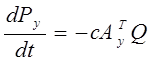 (2)
(2)Рв - матрица потенциалов источников;
Ру – матрица упругих компонентов;
Q – матрица расход в гидромагистрали.
На основании уравнений (1)-(3) выполняется построение динамической математической модели гидравлической системы.
ПРИМЕР ВЫПОЛНЕНИЯ РАБОТЫ
Дана матрица инциденций, представленная в таблице.
Таблица 2 – Матрица инцидентности.
|
Узел |
Ветви |
|||||||||||||||
|
инерционные |
диссипативные |
упр. |
Источники потенциалов |
|||||||||||||
|
m1 |
m2 |
m3 |
m4 |
m5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
-1 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
+1 |
-1 |
0 |
0 |
0 |
0 |
|
2 |
0 |
-1 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
+1 |
0 |
-1 |
0 |
0 |
0 |
|
3 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
+1 |
0 |
0 |
-1 |
0 |
0 |
|
1* |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
-1 |
0 |
-1 |
0 |
0 |
0 |
1 |
0 |
|
2* |
0 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
-1 |
-1 |
0 |
0 |
0 |
0 |
1 |
|
подматри ца |
Аи |
Ад |
Ау |
Ав |
||||||||||||
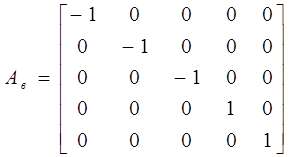 ,
, 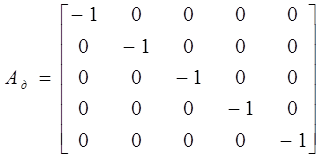 ,
, 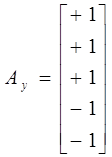 .
.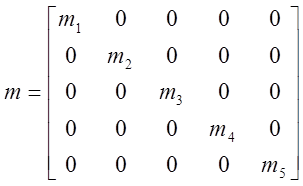 ,
, 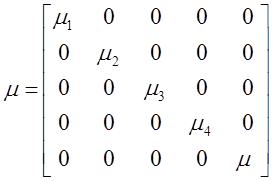 .
.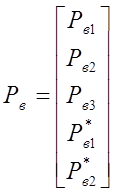 ,
, 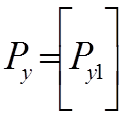 ,
, 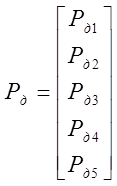 .
.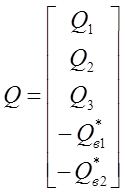
Вычислим матричное произведение слагаемых правой части уравнения (1):
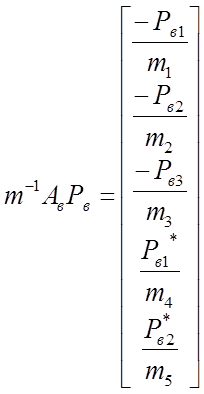 ,
, 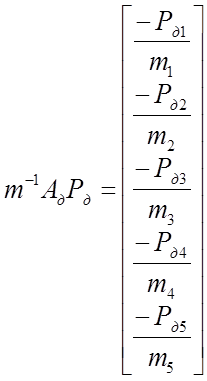 ,
, 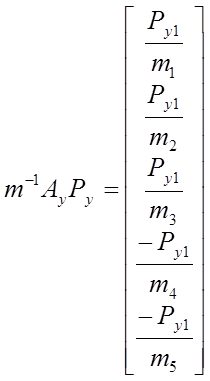 .
.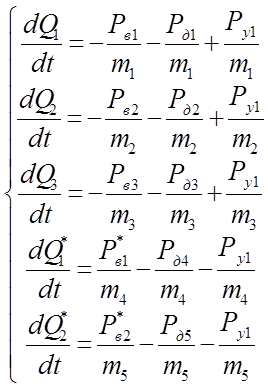
Учитывая, что ![]() , тогда
, тогда ![]() , тогда вместо двух последних уравнений системы, имеем:
, тогда вместо двух последних уравнений системы, имеем:
![]()
![]()
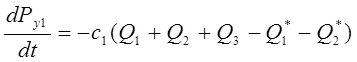
![]()
![]()
![]()
![]()
![]()
Таким образом, математическая модель рассматриваемой гидросистемы, представляется системой, обыкновенных дифференциальных уравнений - и семью алгебраическими выражениями.
Комплексные уравнения, диссипативных элементов носят более сложный характер, при этом выделяют линейные и нелинейные потери давления в гидромагистралях и уравнения, запишется в следующем виде:
![]()
где, ![]() коэффициент гидравлического сопротивления, характеризующий линейные
потери при ламинарном режиме движения жидкости;
коэффициент гидравлического сопротивления, характеризующий линейные
потери при ламинарном режиме движения жидкости;
![]() коэффициент гидравлического
сопротивления, характеризующий нелинейные потери при турбулентном режиме, по
длине и местные.
коэффициент гидравлического
сопротивления, характеризующий нелинейные потери при турбулентном режиме, по
длине и местные.

КОНТРОЛЬНЫЕ ВОПРОСЫ
СПИСОК ЛИТЕРАТУРЫ
4. Бутенин Н. В. Введение в аналитическую механику. —М.: Наука, 1971. — 264 с.
|
Подписано в печать |
Формат 60х84 1/16 |
|
|
Бумага тип |
Усл.-печ.л. 1,25 - печ |
Уч.-изд.л. 1 |
|
Тираж 100 экз. |
Заказ |
Бесплатно |
Саратовский государственный технический университет
410054, г.Саратов, ул.Политехническая, 77
Копипринтер БИТТиУ, 413840, г.Балаково, ул. Чапаева, 140
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.