Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Саратовский государственный технический университет
Балаковский институт, техники, технологии и управления
УЗЛОВОЙ МЕТОД ФОРМИРОВАНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ГИДРАВЛИЧЕСКОЙ СИСТЕМЫ
Методические указания к выполнению практических работ
по курсу "Моделирование систем" для студентов специальности 210100 всех форм обучения
Одобрено
редакционно-издательским советом Балаковского института техники,
технологии и управления
Балаково 2007
|
Для формирования полной математической модели на основе компонентных и топологических уравнений широкое применение получил узловой метод. Для его использования необходимо сформировать матрицу инциденций, отражающую структуру связей всех элементов системы. Матрица инциденций формируется на основании графических моделей технических объектов. Узловой метод имеет классический и модифицированный вариант (для получения модели в нормальной форме Коши). Данные методические указания являются третьей работой по разработке и анализу математических моделей.
ЦЕЛЬ РАБОТЫ
Получение навыков построения математических моделей технических объектов на примере гидравлической системы, используя матрицу инциденций и узловой метод формирования моделей.
ОСНОВНЫЕ ПОНЯТИЯ
Информация о математической модели гидравлической системы, которую содержит орграф, можно представить в виде матрицы инцидентности А, сформированной по следующему правилу.
1. Размерность матрицы α х β:
а) α - число строк соответствует каждому узлу орграфа, за исключением базового;
б) β - число столбцов соответствует ветвям орграфа.
2. Элементы матрицы:
а) отсутствие связи между узлом и ветвью – "0";
б) если ветвь входит в узел – "1";
в) если ветвь выходит из узла – "-1".
При наличии внешнего источника типа потока Q*В он формально заменяется на источник типа потенциала P*B и добавляется условная масса m*B.
Матрицу инциденций А можно представить состоящей из подматриц инерционных АИ, диссипативных АД, упругих АУ ветвей и подматрицы ветвей источников потенциалов АВ.
![]() . (1)
. (1)
Подматрица инерционных элементов АИ всегда единичная диагональная и может быть не отражена при составлении матрицы.
Запишем компонентные уравнения гидравлической системы в матричной форме.
1. Для инерционных элементов
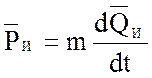 . (2)
. (2)
2. Для диссипативных элементов
![]() . (3)
. (3)
3. Для упругих элементов
![]() . (4)
. (4)
В формулах (2)-(4) использованы следующие обозначения:
![]() -
векторы потенциалов (давлений) соответствующих элементов;
-
векторы потенциалов (давлений) соответствующих элементов;
![]() -
векторы потоков (расходов) соответствующих элементов;
-
векторы потоков (расходов) соответствующих элементов;
![]() -
диагональные матрицы параметров элементов гидравлической системы.
-
диагональные матрицы параметров элементов гидравлической системы.
Топологические уравнения гидравлической системы:
1. Уравнение равновесия потенциалов ветвей орграфа, инцидентных i-ому узлу:
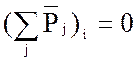 ,
, ![]() . (5)
. (5)
2. Уравнение непрерывности фазовой переменной типа потока l-ой ветви:
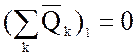 ,
, ![]() . (6)
. (6)
В формулах (5), (6) n – число узлов орграфа, за исключение базы, l – число ветвей.
Используя матрицу инциденций уравнения (5), (6), можно записать в матричной форме:
![]() ; (7)
; (7)
![]() ; В=И, Д, У, (8)
; В=И, Д, У, (8)
где А – матрица инциденций;
АТ – транспонированная матрица инциденций;
![]() -
вектор потоковых переменных ветвей;
-
вектор потоковых переменных ветвей;
![]() -
вектор потоковых переменных узлов.
-
вектор потоковых переменных узлов.
Отдельный элемент ![]() вектора
вектора ![]() определяется
по формуле:
определяется
по формуле:
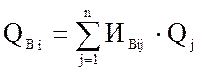 , (9)
, (9)
где ![]() -
элемент матрицы инциденций, характеризующий соответствии i-ой ветви орграфа j-ому узлу.
-
элемент матрицы инциденций, характеризующий соответствии i-ой ветви орграфа j-ому узлу.
Вектор потенциалов системы ![]() представим состоящим из-под векторов
инерционных, диссипативных, упругих элементов и внешних воздействий на систему
представим состоящим из-под векторов
инерционных, диссипативных, упругих элементов и внешних воздействий на систему
![]() . (10)
. (10)
Тогда, используя (1), уравнение (7) запишется в виде
![]() . (11)
. (11)
С учетом (2)-(4) уравнение (11) принимает вид
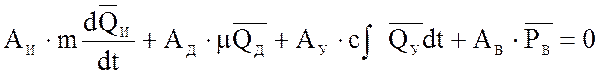 . (12)
. (12)
Учитывая топологическое уравнение (8),
фазовые переменные ![]() ,
, ![]() ,
,
![]() можно выразить через узловые
потоковые переменные
можно выразить через узловые
потоковые переменные ![]() . В результате получают
матричное уравнение, являющееся классическим вариантом узлового метода:
. В результате получают
матричное уравнение, являющееся классическим вариантом узлового метода:
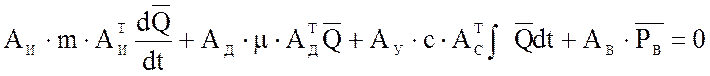 . (13)
. (13)
Для перехода к системе дифференциальных уравнений в нормальной форме Коши выполняют следующие преобразования:
1. Подставляют значения ![]() в уравнение (13) и разрешают его
относительно производной.
в уравнение (13) и разрешают его
относительно производной.
2. Определяют производную по времени от
вектора ![]() и сводят в единую систему:
и сводят в единую систему:
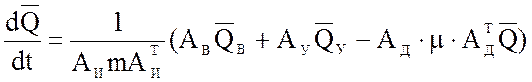 , (14)
, (14)
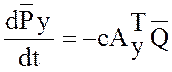 . (15)
. (15)
Так как матрицы АИ и m одного и того же порядка, то матричное произведение
![]() . (16)
. (16)
Тогда система (14), (15) запишется в виде:
 ; (17)
; (17)
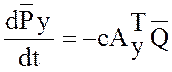 ,
(18)
,
(18) 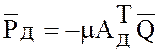 . (19)
. (19)Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.