ТЕСТ по ОПД.Ф.09 «МОДЕЛИРОВАНИЕ СИСТЕМ»
для специальности
«Управление и информатика в технических системах»
5 вариантов по 15 вопросов
ВАРИАНТ 1
1. Уравнения математической физики, не зависящие от времени называются …
2. Граничные условия для уравнений математической физики имеют вид:
1) 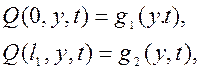
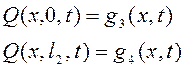 3)
3) 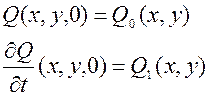
2) ![]() 4)
4)
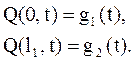 ;
;
3. Компонентные уравнения инерционных элементов имеют вид:
1) ![]()
2) 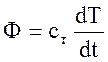
3) ![]()
4) 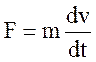
4. Определить вид уравнения диссипативного элемента разных типов систем
1) гидравлической системы
1) ![]()
2) тепловой системы
2) ![]()
3) механической вращательной системы
3) ![]()
4) механической поступательной системы
4) ![]()
5. Расположить по порядку этапы анализа систем с распределенными параметрами
1) идентификация начальных и граничных условий;
2) определение стандартизирующей функции и функции Грина;
3) выбор уравнения математической физики;
4) расчет функции состояния.
6. Элемент на макроуровне, отображающий свойства рассеивания энергии конструктивными элементами технического объекта, обусловленные силами внутреннего трения, пропорциональными относительной скорости перемещения взаимодействующих сосредоточенных масс называется:
1) инерционным элементом;
2) диссипативным элементом;
3) базовым элементом;
4) упругим элементом.
7. Топологические уравнения описывают:
1) зависимость между переменными типа потока и типа потенциала;
2) условия равновесия фазовых переменных;
3) аппроксимацию моделей микроуровня;
4) условия равновесия и непрерывности фазовых переменных.
8. При имитационном моделировании используется математическая модель:
1)воспроизводящая алгоритм (логику) функционирования исследуемой системы во времени при различных сочетаниях значений параметров системы и внешней среды;
2) в форме алгебраических, дифференциальных и других уравнений, связывающих выходные переменные с входными, дополненных системой ограничений;
3) в графической форме, отражающая структуру и связи элементов системы;
4) в форме дифференциальных уравнений в частных производных с начальными и граничными условиями.
10. Вид уравнения Лапласа:
1) 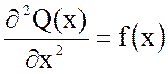
![]() 3)
3) 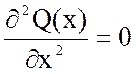
![]()
2) ,
,![]() 4)
4)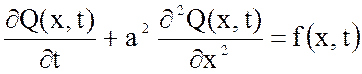 ,
,![]() ,
, ![]()
11. Модели по изменению переменных во времени подразделяются на:
1) теоретические и формальные;
2) статические и динамические
3) стохастические и детерминированные;
4) адаптивные и неадаптивные.
1) компонентные уравнения гидравлической системы;
2) топологические уравнения тепловой системы;
3) инерционное уравнение электрической системы;
4) топологические уравнения электрической системы.
13. Наивысший порядок производной по времени t в уравнениях гиперболического типа?
1) первый;
2) третий;
3) второй;
4) отсутствует.
14. Уравнение 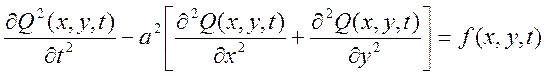 можно охарактеризовать как:
можно охарактеризовать как:
1) неоднородное уравнение гиперболического типа в двух мерных декартовых координатах
2) однородное уравнение гиперболического типа в трех мерных сферических координатах
3) неоднородное уравнение параболического типа в двух мерных декартовых координатах
4) неоднородное уравнение гиперболического типа в трех мерных декартовых координатах
15. Граничные условия первого рода носят название:
1) Лапласа;
2) Неймана;
3) Гельмгольца;
4) Дирихле.
ТЕСТ по ОПД.Ф.09 «МОДЕЛИРОВАНИЕ СИСТЕМ»
для специальности
«Управление и информатика в технических системах»
5 вариантов по 15 вопросов
ВАРИАНТ 2
1. Уравнения … типа описывают колебательные процессы различной физической природы во времени.
2. Начальные условия для уравнений математической физики имеют вид:
1) 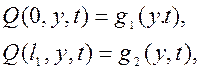
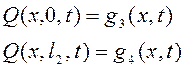 3)
3) 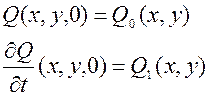
2) ![]() 4)
4)
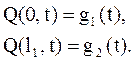 ;
;
3. Компонентные уравнения упругих элементов имеют вид:
1) ![]() 2)
2)
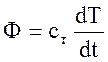 3)
3) ![]() 4)
4) 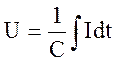
4. Охарактеризовать тип граничных условий
1) неоднородные условия первого рода (задача Дирихле)
1) ![]()
![]()
![]()
2) неоднородные условия второго рода (задача Неймана)
2)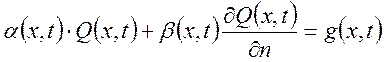
![]()
3) однородные условия первого рода
3) ![]()
![]()
![]()
4) неоднородные условия третьего рода (смешанная задача)
4) 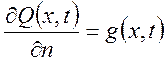
![]()
![]()
5. Расположить по порядку этапы моделирования
1) Исследование модели в соответствии с поставленной целью.
2) Выбор модели.
3) Проверка адекватности объекта и модели.
4) Постановка задачи и определение свойств реального объекта, подлежащего исследованию.
6. Иерархический уровень моделирования, где объект рассматривается как динамическая система с сосредоточенными параметрами, а математическая модель имеет вид обыкновенных дифференциальных уравнений, называется:
1) макроуровень;
2) микроуровень;
3) мегауровень;
4) метауровень.
7. Физический или абстрактный образ моделируемого объекта, удобный для проведения исследований и позволяющий адекватно отображать интересующие исследователя физические свойства и характеристики объекта называют:
1) аналогом;
2) моделью;
3) прототипом;
4) элементом.
8. Модель, используемая для описания обобщенных систем и представляющей собой формальную схему общего вида, называется:
1) агрегативной;
2) математической;
3) общей;
4) условной.
9. Начальные условия краевой задачи описывают:
1) функцию состояния в начальный момент времени на границе области;
2) функцию состояния в начале координат;
3) функцию состояния в начальный момент времени на всей пространственной области;
4) нулевое входное воздействие.
10. Программной средой моделирования задач математической физики является:
1) Microsoft Excel;
2) PDE Tool;
3) Simulink;
4) Acrobat Reader.
11. Для гиперболического
уравнения 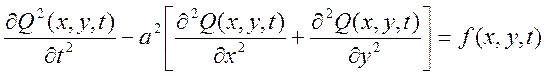 граничные условия имеют
вид:
граничные условия имеют
вид:
1) 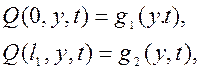
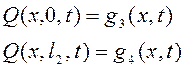 3)
3) 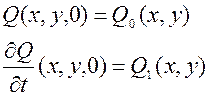
2) ![]() 4)
4)
![]() ;
;
![]() ;
;
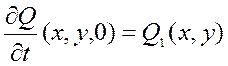 .
.
12. Определяющим признаком статического режима для технической системы любой физической природы является:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.