1) постоянство во времени всех фазовых переменных, характеризующих состояние всех ее элементов;
2) изменение во времени всех фазовых переменных элементов;
3) постоянство во времени всех фазовых переменных, характеризующих состояние хотя бы одного ее элемента;
4) равенство нулю хотя бы одной фазовой переменной.
13. Полная погрешность численных методов интегрирования включает следующие составляющие:
1) погрешность аппроксимации, вычислений (округлений в ЭВМ), накопления;
2) погрешность аппроксимации и накопления;
3) погрешность аппроксимации и вычислений (округлений в ЭВМ);
4) погрешность вычислений (округлений в ЭВМ) и накопления.
14. Физический подход при построении теоретических моделей заключается:
1) в использовании общих математических принципов;
2) в исследовании физической модели;
3) в установлении в процессе эксперимента связей между отдельными параметрами;
4) в непосредственном применении физических законов.
15. К какому классу относится волновое уравнение:
1) гиперболические; 3) эллиптические;
2) параболические; 4) смешанные.
ТЕСТ по ОПД.Ф.09 «МОДЕЛИРОВАНИЕ СИСТЕМ»
для специальности
«Управление и информатика в технических системах»
5 вариантов по 15 вопросов
ВАРИАНТ 3
1. Уравнение колебаний мембраны относится к уравнениям … типа.
2. Однородные уравнения математической физики имеют вид:
1)
, 
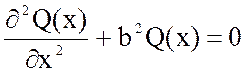2)
,
, 
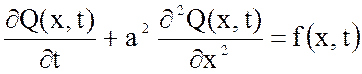3)
,
,
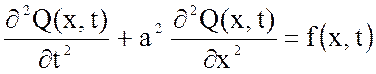4)
,
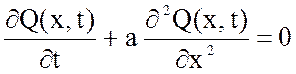
3. Условия однозначности решения дифференциальных уравнений в частых производных
1) граничные условия; 2) неоднородные условия;
3) начальные условия; 4) нулевые условия.
4. Определить вид уравнения инерционного элемента разных типов систем
1) гидравлической системы
1) 
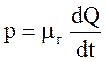
2) электрической системы
2) 
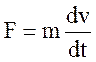
3) механической вращательной системы
3) 
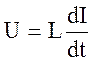
4) механической поступательной системы
4) 
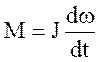
5. Расположить по порядку этапы метода Ньютона для решения систем нелинейных уравнений:
1) Вычисление нормы вектора невязок и проверка условий окончания итерационного процесса
2) выбор
начального приближения вектора искомых фазовых переменных 
3)
Определение нового приближения вектора искомых фазовых переменных: 
4) вычисление матрицы Якоби в
точке 
, вектора невязок 
и вектора поправок 
6. Компонентное уравнение упругого элемента есть:
1) линейная зависимость между переменными
2) дифференциальная зависимость между переменными;
3) интегральная зависимость между переменными;
4) неоднозначная зависимость.
7. Задачи, решаемые при анализе статических состояний:
1) интегрирование системы дифференциальных уравнений, определение показателей качества;
2) оценка физических свойств технической системы без решения системы уравнений математической модели, выбор методов численного решения уравнений модели;
3) моделирование случайных величин и случайных процессов с заданными вероятностными характеристиками;
4) определение положений устойчивого равновесия системы, определение начальных и конечных условий при оценке качества переходных процессов по переходным характеристикам, анализ распределения фазовых переменных на установившихся равновесных режимах функционирования.
8. На основании закона Ома получают:
1) топологические уравнения электрической системы;
2) уравнение диссипативного элемента электрической системы;
3) инерционное уравнение электрической системы;
4) топологические уравнения тепловой системы.
9. К какому классу относится уравнение Гельмгольца:
1) параболические; 2) гиперболические; 3) смешанные; 4) эллиптические.
10. Данное выражение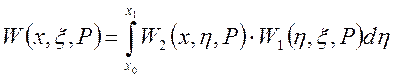 
описывает:
1) параллельное соединение распределенных блоков;
2) соединение распределенных блоков в виде обратной связи;
3) последовательное соединение распределенных блоков;
4) последовательное соединение распределенного и сосредоточенного блоков.
11. Системы, состояния которых описывается функциями нескольких аргументов, зависящих как от времени, так и от пространственных координат, имеют название:
1) системы с пространственными параметрами;
2) системы с распределенными параметрами;
3) системы с сосредоточенными параметрами;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.