Современные тенденции развития средств вычислительной техники. Классификация средств ЭВТехники. Цели и задачи создания ЭВМ, страница 7

1)  ДСНФ (дизъюнктивная совершенная нормальная форма)

2)  КСНФ (конъюнктивная совершенная нормальная форма)

Аналитическая запись ПФ в ДСНФ и КСНФ строится по средствам суперпозиции (наложения) специальных вспомогательных функций (минтермов m_i и макстермов М_i)

Минтерм – (констентуента единицы) – булево произведение (конъюнкция) от n переменных, в котором каждая переменная входит только один раз, либо в ПК (если ее значение в данном наборе равно 1), либо в инверсном (если значение переменной в наборе равно 0)

Макстерм М_i – (констентуэнта нуля) – булева сумма (дизъюнкция) от n переменных, в который каждая переменная входит только 1 раз в прямом или инверсном виде.

Число макстермов и минтермов равно числу аргументов, на которых функция определена.

Таким образом алгебраическое выражение для любой переключательной функции можно представить в форме:

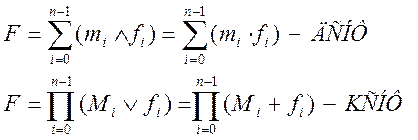
В принципе обе формы эквивалентны. Выбор формы представления зависит от числа наборов, на которых функция равна 1, либо равна 0.

Где больше 1 – ДСНФ

Где больше 0 – КСНФ.

Однако при минимизации ПФ более удобной является ДСНФ.

i	переменные		минтерм				макстерм
	X1	X2	m0	m1	m2	m3	M0	M1	M2	M3
0	0	0	1	0	0	0	0	1	1	1
1	0	1	0	1	0	0	1	0	1	1
2	1	0	0	0	1	0	1	1	0	1
3	1	1	0	0	0	1	1	1	1	0

в) при относительно небольшом числе элементов (не более 6) в ряде случаев удобным и наглядным является графическое представление ПФ в виде т.н. карт минтермов.

Наиболее распространенная форма – карта Карно.

Карта Карно содержит 2ⁿ клеток, каждая из клеток соответствует одному из минтермов. (q=2ⁿ)

Если требуется представить на карте Карно (кК) функцию, заданную в виде ДСНФ, то в клетках карты для минтермов, входящих в ДСНФ ставится 1, иначе – 0 или оставляются незаполненными.

Существует целый класс, значение которых определено для части наборов аргументов (они называется частично определенные ПФ)

Наборы, для которых ПФ определена – рабочие.

Наборы, для которых ПФ неопределенна – безразличные (в табл. обозначены крестиком). На практике безразличные режимы не реализуются.

Упрощение (минимизация) ПФ

Чем проще логическое выражение для ПФ, тем меньше элементов требуется для ее технической реализации.

Под минимизацией ПФ подразумевают нахождение для нее такой ДНФ, которая имеет минимальную цену или сложность.

Общие методы решения задачи минимизации денежной стоимости цифровых устройств отсутствуют. Наиболее часто процесс минимизации (м.) рассматривается в упрощенной постановке, как поиск дизъюнктивных форм ПФ, содержащих наименьшее число переменных.

Методы минимизации ПФ.

В настоящее время известен целый ряд методов м. в ПФ. Все они основаны на преобразовании логических выражений и подразделяются на систематические и несистематические.

а) систематические методы

Достоинство – их полная формализация, т.е. они, описываются строгими алгоритмами. Многие из них реализованы в виде стандартных программ для ЭВМ. К числу наиболее распространенных систематических методов относится метод Квайн-Маккласки.

Нахождение минимальной формы производится в 3 этапа:

1. анализируется вид задания ПФ

Если она задана произвольной формой в булевой алгебре, то с помощью законов алгебры логики она приводится в ДСНФ.

2. нахождение сокращенной ДСНФ с использованием операций склеивания и поглащения. Если в формуле ПФ присутствуют минтермы, отличные друг от друга формой вхождения только одной переменной, то такие минтермы называются смежными (соседними)

Смежные минтермы могут быть попарно склеенными. Результат склеивания – это имбликата, которая представляет собой конъюнкцию, число аргументов в которой на 1 меньше, чем в исходном минтерме.

Обычно в процессе м. склеивают смежные минтермы, затем – имбликаты. Процесс длится до получения имбликат, которые не склеиваются между собой. Такие имбликаты называются простыми, состоящими из дизъюнкции простых импликат, называемых сокращенной ДНФ.

Может показаться, что в сокращенную ДНФ входят имбликаты, наличие или отсутствие которых не сказывается на значение функции. Такие простые имбликаты – избыточные. Если в сокращенной ДНФ удалить все избыточные имбликаты, то получают тупиковую ДНФ.

Искомая минимальная ДНФ совпадает с той из тупиковой, которая содержит наименьшее число вхождений аргументов.

б)несистематические методы

(Метод Квайна Мак Класки – при большом числе переменных, >6. При n≤6 наиболее простым является метод Вейч-Карно, основанный на табличном представлении ПФ.

Карты Карно (диаграмма Вейча) – это прямоугольные таблицы, состоящие из 2ⁿ клеток.

Для задания ПФ надо в каждую клетку занести значение функции, которое она принимает на соответствующем наборе аргументов.

Клетки, содержащие 1 (единица-клетка) –соответствует определенному минтерму. Если в соседних клетках содержится 1, то надо объединить соответствующие минтермы в имбликаты. Такое объединение клеток эквивалентно операции склеивания минтермов, получается более простое выражение для ПФ.

Объединенные клетки будут соответствовать имбликатам, дизъюнкции которых содержат сокращенную ДСНФ:

1	1	0	1
0	0	0	0
0	0	1	1
0	0	0	1