А=an-1qn-1+ an-2qn-2+…+ a0q0+…+ a-mq-m (1)
Коэффициентами этого полинома являются числа базовой СС. Пользуюясь взаимно однозначным соответствием может быть сокращенное обозначение:
А=(an-1 an-2 … a0 . а-1 … a-m )(q) (2)
Чтобы произвести запись числа А в выбранной СС, необходимо представить его в виде полинома, затем записать коэффициенты этого полинома в виде последовательности (2).
В общем случае, понятие число и запись числа имеет разный смысл. В повседневной практике вычисление выполняется обычно с записями числе.
Под числом подразумевается запись числа и поэтому на практике часто пользуются условным равенством:
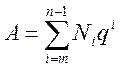
Числовое значение цифры определяется позицией, которую она занимает в записи, величиной q, определяющей числовое значение цифры qi в i-ом разряде.
При
этом разрядности 
0 называются старшими, а с
меньшими номерами у данного – младшими.
Точка в выражении (2) разделяет на целую и дробную часть.
Только с помощью комбинации (3) нельзя определить конкретный вид числа, для получения конкретного числового значения, т.е. для расшифровки (2) необходимо доп. указать основание СС q ( 10 – по умолчанию)
В ЭВМ и цифровых системах оперируют с числами, представленными в 2-чной СС, что обусловлено аппаратной частью этих устройств, реализующихся на основе бистабильных элементов.
При разработке программ для ЭВМ в качестве вспомогательных систем используют также 8 и 16-чные СС.
Представление чисел в различных СС допускает их взаимнооднозначное преобразование.
В ЭВМ перевод из одной СС в другую выполняется автоматически по спец. алгоритмам. При этом правила перевода целых и дробных чисел отличаются др от друга.
Рассмотрим формализованные процедуры перевода из 10чной в S-ичную CC:
A(10)® A(S)
Алгоритм перевода целых.
1. основание S новой СС необходимо представить его 10-чным изображением (в 10чной СС)
2. разделить исходное целое на основание S по правилам 10й арифметики. В остатке – число a0 младшего разряда искомой записи.
3. Частное, полученное от делелния (п.2) снова делятся на S, в остатке – а1.
4. выполнять п.3 до тех пор, пока в частном не получится 0. Последний остаток аn-1
AS=an-1Sn-1+…+a0S0
Алгоритм перевода 10чных дробных в Sичную СС.
Пусть задана правильная 10чная дробь.
A(S)др=0,а1·S-1… а-m·S-m
1. S®S(10)
2. Умножить исходную дробь на S по правилам 10чной арифметики. При этом целая часть – цифра старшего разряда (а-1)
3. дробную часть, полученную на предыдущем шаге произведения снова умножаем на S. Целая часть нового произведения – очередная цифра a-2
4. выполнять п.3 до тех пор, пока точность искомого S-представления исходной 10ой дроби окажется не хуже ее исходного 10ого представления.
Алгоритм перевода смешанной 10ой дроби в Sчную СС.
Смешанная 10ая дробь переводится в вариант с основанием S по частям, выполняя раздельно для целой и дробной частей.
При переводе чисел из СС с основанием q в основание S никаких вычислений не требуется, если выполняется соотношение q=Sk
1. k>0. Каждую цифру А(q) заменить ее Sчным цифровым значением, длинной k разрядов.
A(16)=3B.D
q=16; S=2; k=4
S(2)=0011 1011. 1101
3 B D
2. k<0 каждую группу из k-чных цифр заменяют одной цифрой S-чной CC,
двигаясь от точки вправо и влево.
Правила сложения 2чных чисел
Достоинство позиционных СС заключается в простоте выполнения ариф. операций, причем алгоритм в позиционной СС унифицированный, поскольку сложение 2х чисел – основа всех операций в ЭВМ.
А(2)+B(2)=C(2)
A(2)=an-1 an-2 … a0 . a-1 … a-m
B(2)=bn-1 bn-2 … b0 . b-1 … b-m
C(2)=cn-1 cn-2 … c0 . c-1 … c-m
Cкладываются числа по разрядам (столбиком), начиная с младших разрядов, результат – i-ом разряде будет 2 объекта: цифра Сi и перенос Pi+1 в соседний младший разряд
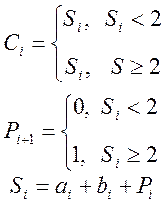
Следовательно в суммировании участвуют 3 цифры ai, bi и перенос Pi
2 этапа:
1) аi+Pi
2) +bi
Форма представление чисел в цифровых устройствах и ЭВМ
В ЭВМ оперируют с изображениями чисел конечной длины, т.к. ЭВМ имеет ограниченную длину разрядной сетки, что накладывает ограничения на диапазон и точность обрабатываемой величины.
Общее количество чисел, которые можно изобразить l разрядной записью составляет 2l.
При разработке ЭВМ и цифровых устройств конкурируют 2 тенденции:
Конкуренция указанных тенденций привела к использованию в ЭВМ 2х форм представления чисел:
1. когда нужен мин. объем оборудования – использование представление чисел с фиксированной точкой (ЧФТ)
2. если более важным является высокая точность, применяют числа с плавающей точкой (ЧПТ)
А=an-1qn-1+ an-2qn-2+…+
a0q0+a-1q-1…+ a-mq-m=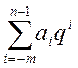
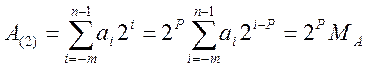
MА – мантисса числа, Р – порядок числа.
Представление чисел с фиксированной точкой.
Представление чисел в форме с фиксированной точкой предполагает отображение числа только с помощью МА, а порядок 2Р исключается из обработки.
Использование ЧФТ требует большой подготовительной работы на этапе подгонки задачи к ее решению, т.к. алгоритм решения задачи разрабатывается так, чтобы операндами вычисления выступает только МА.
При этом фиксированная точка в машине физически никак не отображается, о ее расположение как и о величине порядка Р знают только разработчики и пользователь, интерпретирующий результат вычисления.
Т.к.
пределы изменения большинства переменных решаемой задачи (особенной
промежуточных вычислений) при начале вычисления не известны, то нет полной
гарантии, что результаты будут укладываться в пределах разрядной сетки. Если 
при работе с правильными дробями или 
при работе с целыми мантиссами,
говорят, что имеет место переполнение разрядной сетки или выход за пределы разрядной
сетки влево.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.