Наиболее опасно в этом отношении операции сложения чисел с одинаковыми знаками, т.к. за пределы разрядной сетки могут выйти и будут потеряны старшие разряды суммы, появится искажение результата и может быть чревата тяжелыми последствиями.
При умножении l разрядных сомножителей получится произведение, длиной в 2l разряда. Если сомножители целы, то их произведение заведомо переполняет разрядную сетку, если правильные дроби – то переполнение не влево, а само 2l разрядное произведение округляется до стандартной длины, этим объясняется факт, что в машинах с ЧФТ работают с правильными дробями.
Вместе с тем, при умножении правильных дробей можно получить 2l разрядный результат, у которого старшие l разряды – нули. Если после округления такого результата в этих разрядах нули, то выход результата за пределы разрядной сетки вправо. Такой результат равен нулю (машинный ноль)
0,00000000000501
Для предотвращения переполнения разрядной сетки в ЭВМ с ЧФТ работающих с правильными дробями предусматривают тех и программные средства для обнаружения случаев переполнения разрядной сетки.
Масштабирование.
При математической формулировке реальных тех и физ. задач приходится иметь дело не только с относительными безразмерными величинами, а с физическими переменными, имеющими те или иные размерности. Поэтому в ЭВМ каждая физ. величина АФ представляется соответствующей машинной переменной АМ
АФ® АМ – связь осуществляется посредством использования масштаба.
Т.е. происходит масштабирование переменных решаемой задачи.
Если решение задачи осуществляется на ЭВМ с ЧФТ, то масштабирование совмещают с процедурой представления данных в форме чисел с фиксированной точкой.
Масштаб:
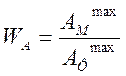
АФ
задается с точностью до некоторого значения 
,
поэтому в интервале [0;AФmax] общее число различных
значений переменной составляет: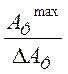 
Для двоичной записи любого из этих значений потребуется некоторое значение l порядков:
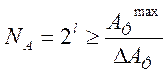, l – длина
разрядной сетки.
Представление в ЭВМ данных в виде ЧФТ позволяет исключить из обработки порядки данных. Этим достигается уменьшение объема оборудования и увеличение скорости вычислений, в чем заключается основное достоинство представления данных в форме с фиксир. точкой.
Представление чисел в форме с плавающей точкой (ЧПТ).
В этом случае числа представляются как с использованием мантиссы, так и порядка.
A=2PMA
В ЭВМ с ЧПТ запись любого числа состоит из двух полей:
Т.к. основание в 2ой СС равно 2, является величиной фиксированной, то для представления множителя 2P нужен лишь порядок
Представление числа А≠0 в форме с плавающей точкой является неоднозначным:
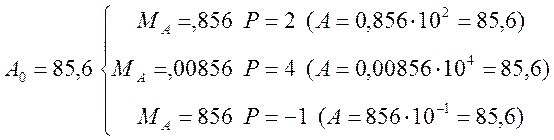
Для получения однозначного представления числа в выбранной Sчной СС порядок числа Р для А≠0 выбирается так, что S-1≤MA<1
В этом случае говорят, что мантисса должна быть правильной дробью, а-1≠0
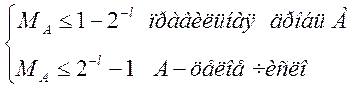
Основное достоинство ЧПТ в том, что при длине разрядной сетки 30-32 разряда не возникает проблем для вышеперечисленный условий.
В современных микропроцессорах обеспечивается диапазоны от Аmin до Аmax, где
Аmin=10-306
Аmax=10306
Масштабирование сводится к нормированию переменных задачи так, чтобы ЭВМ работала с безразмерными величинами, т.е. для каждой из этих величин порядок Р выбирается так, чтобы мантисса была нормализована.
Относительная погрешность ЧПТ существенна ýже диапазона значений для погрешностей с ЧФТ.
Недостатком ЧПТ является меньшая производительность ЭВМ с этой формой чисел (при одинак. элементной базе). Потеря производит. при работе с ЧПТ вызвана необходимостью оперирования не с мантиссой, а с порядком.
Еще одной (третьей) формой представления чисел в ЭВМ является двоично-десятичная. При обработке больших массивов десятичных чисел (экономические расчеты) приходится тратить много времени для перевода в 2ую СС для обработки на ЭВМ и обратный перевод. Кажд такой перевод – это 20-40 машинных команд.
Если включать в состав ЭВМ специальные функциональные блоки или сопроцессоры десятичной арифметики, то появляется возможность обрабатывать десятич. числа напрямую (возрастает скорость вычисления). При этом кажд 10ая цифра представляется 2ой тетрадой:
А(10)=3759®А(2-10)=0011 0111 0101 1001
Положение точки заранее фиксируется.
Знаки:
+ = 1100
- = 1101
Арифметические операции над числами в ЭВМ
Машинные коды чисел
Современные ЭВМ имеют развитую систему команд, включающую сотни машинных операций, при этом выполнение люб. операций может быть сведено к использованию простейших микроопераций «сложение» и «сдвиг», что позволяет иметь универсальное АЛУ для выполнения люб. операции, связанных с обработкой.
Во всех ЭВМ все операции выполняются над числами, представленными специальными машинными кодами. При этом, чтобы исключить трудности, связанные с необходимостью учета знаков при выполнении алгебраических операций. Алгебраические величины отображают на счетное упорядоченное множество положительных чисел. В зависимости от способа отображения различают след коды:
ПК – прямой код
ДК – дополнительный код
ОК – обратный код
Использование этих кодов позволяет применять и обрабатывать знаковые разряды чисел так же, как и значащие разряды этих чисел, а также заменять операцию вычитания сложением.
В наст. время ОК применяют редко
1) Прямой код двоичного числа образуется из абсолютного значения его и знака в старшем разряде (0+,1-)
0 0000101
1 0000101
2) Обратный код положительных чисел совпадает с ПК. ОК отрицательных чисел имеет 1 в старшем разряде, но значащие – инверсные.
Недостатком ОК является то, что в нем число 0 может быть как положительным числом, так и отрицательным(00000…0, 11111…1)
Из-за этой неоднозначности вместо ОК используют ДК.
3)Дополнительный код положительных чисел совпадает с ПК. ДК отрицательных чисел – результат суммирования ОК числа с единицей младшего разряда.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.