Современные тенденции развития средств вычислительной техники. Классификация средств ЭВТехники. Цели и задачи создания ЭВМ, страница 6

Всякая булева функция имеет свои пределы, обл определения, охватывающая совокупность комбинаций ее переменной. Каждое возможное совпадение аргументов – это набор. Так как всякая переключательная функция может принимать только два значения, то при n  переменных 2ⁿ наборов, а число булевых функций N=2².

n=0  N=2

n=1  N=4

n=2  N=16

n=3  N=256

n=4  N=65536

Если неизвестно какие значения принимает булева функция на всех наборах аргумента, то она называется недоопределенной (частичной), а набор аргументов – запрещенные наборы. Значение функции на запрещенных наборах можно задать желаемым образом.

ПРИЛОЖЕНИЕ 1.

Законы алгебры логики (Булева алгебра)

1. Закон одинарных элементов:

2. Закон отрицания (противоречия):

3. Закон двойного отрицания:

4. Комбинационные законы:

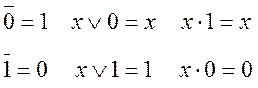
а)тавтология (повторение):

б)Коммутативный (переместительный):

в)Ассоциативный (сочетательный):

г)Дистрибутивный (распределительный):

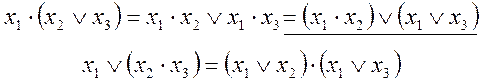 а если подставить 011??

д) Поглощения:

е) Склеивания:

5. Законы дуальности (инверсии, двойственности) (теорема де Моргана)

6. Обобщенные законы дуальности (т. К. Шеннона):

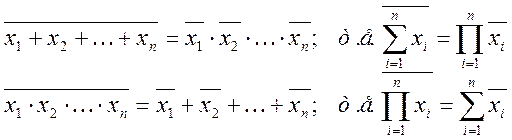
ПРИЛОЖЕНИЕ 2.

Булевы функции двух переменных: F_i=F_i(x₁,x₂),  i=0…(n-1)

i	Fi	Наборы переменных					Условное обозначение и алгебраическое выражение	Название функции
		x1	0	0	1	1
		x2	0	1	0	1
0	F0		0	0	0	0		константа 0
1	F1		0	0	0	1		конъюнкция (лог. «и»)
2	F2		0	0	1	0		запрет (на х2)
3	F3		0	0	1	1		тождественность (переменная) х1
4	F4		0	1	0	0
5	F5		0	1	0	1		переменная (тождественность) Х2
6	F6		0	1	1	0		Неравнозначность (сложение по модулю 2)
7	F7		0	1	1	1		дизъюнкция (лог. «или»)
8	F8		1	0	0	0		Функция Вебба (или-не) (стрелка Пирса)
9	F9		1	0	0	1		Равнозначность (эквивалентность)
10	F10		1	0	1	0		отрицание (инверсия, лог. «не») переменной х2
11	F11		1	0	1	1		Импликация от х2 к х1
12	F12		1	1	0	0		отрицание (инверсия) х1
13	F13		1	1	0	1		импликация от х1 к х2
14	F14		1	1	1	0		Операция («штрих») Шеффера («и-не»)
15	F15		1	1	1	1		константа 1

Из функции, представленной в приложении 2, (F_i(x₁,x₂), i=0…15) можно строить сколь угодно сложные зависимости, отражающие алгоритмы преобразования информации, представленной в системе (2).

Возможен ли набор таких простых булевых функций, на основе которых можно получить любую, сколь угодно сложную функцию?

Одним из основных понятий булевой алгебры является понятие функциональной полноты булевой функции (БФ)

Система БФ называется полно, если на ее основе можно получить любую функцию, используя лишь операции суперпозиции.

Алгебра логики дает несколько наборов БФ обладающие функциональной полнотой и образующих полный базис простейших функций, из которых могут строятся любые более сложные. Одним из них является набор 3-ёх БФ, носящих название «основного, функционального, полного набора»

А: {F₁=(x₁·x₂) – конъюнкция; F₇=(x₁+x₂) – дизъюнкция; F₁₂=- инверсия}

В общем случае, одна из этих функций является избыточной, т.е. ее исключение из набора не нарушает функциональной полноты:

B: {F₁;F₁₂}, C:{F₇;F₁₂} – функционально полные, т.к. на их основе можно получить любую исключенную из набора функцию.

Однако использование сокращенных базисных наборов требует от разработчика значительных навыков.

Способы задания переключательных функций

Задать переключательную функцию (ПФ) – значит указать ее значение при всех возможных наборах ее аргументов. Логические функции в общем случае могут иметь различные формы представления: словесное, табличное, алгебраическое, графическое (например, карта Карно).

а) табличный способ задания ПФ

Самым простым и наглядным является табличный способ, в котором составляется таблица с указанием всех наборов аргументов и значений функций для них.

Эта таблица называется таблицей истинности или таблицей соответствия.

Кроме наглядности табличный способ обладает тем достоинством, что каждой функции соответствует одна и только одна таблица истинности. Недостаток табл. способа – громоздкость таблицы истинности, растет с возрастанием числа переменных: n=6, 2⁶ строк.

Кроме того, эта форма не позволяет выяснить каким образом следует реализовать и можно ли упростить данную функцию.

б)  аналитический способ (алгебраический)

Для реализации и последнего упрощения ПФ, их следует представить в аналитической форме, т.е. в принципе можно представить различными аналитическим выражениями. Доказано, что применительно к основному функциональному полному набору (содержащему конъюнкцию, дизъюнкцию и инверсию) любая ПФ, предварительно заданная в табличном виде может быть записана аналитически в двух формах, называемых каноническими (нормальными):