Синтез систем управления механическим объектом

Министерство науки и образования РФ

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Кафедра АПУ

СИНТЕЗ СИСТЕМ  УПРАВЛЕНИЯ МЕХАНИЧЕСКИМ ОБЪЕКТОМ.

Пояснительная записка к курсовому проекту по дисциплине "Теория Автоматического Управления".

Выполнили: Студенты группы 5321

                                    Проверил:

                                       Проф. Имаев  Д.Х

Санкт-Петербург

2008 г.

Содержание.

Введение                                                                                                                  

1. Механическая система, как объект управления                                         

1.1 Описание объекта управления.                                                                 

1.2 Математическая модель объекта управления.                              

        1.3 Дифференциальные уравнения в форме Коши.

        1.4 Линеаризация дифференциальных уравнений объекта управления.         

2. Анализ объекта управления                                                                           

2.1 Компьютерная имитация объекта управления.                                      

2.2 Линеаризация модели.                                                                              

2.3 Анализ устойчивости положения равновесия.                             

2.4 Анализ управляемости и наблюдаемости объекта.                                

2.5 Передаточная функция объекта.                                                              

3. Синтез регуляторов                                                                                                     

3.1 Синтез регуляторов состояния.                                                                

3.2 Синтез наблюдателя состояния объекта.                                                

3.3 Динамический регулятор.                                                               

3.4 Компьютерное моделирование системы “Нелинейный объект плюс линейный регулятор”.                                                                      

3.5 Попытка расширения области притяжения положения равновесия.                                        

1. МЕХАНИЧЕСКАЯ СИСТЕМА, КАК ОБЪЕКТ УПРАВЛЕНИЯ.

1.1 Описание объекта управления.

Объект представляет собой подвижную каретку с перевернутым маятником, как это показано на рис 1.1. Неустойчивая механическая система имеет две степени свободы. На рис 1.1 приняты следующие обозначения: M – масса каретки, кг; m – масса маятника, кг; l – длина маятника, м; 𝜃 – угол отклонения маятника, рад; x – положение каретки, м; f – сила, Н.

Примем следующие параметры механического объекта: l = 1 м; m = 1 кг; M=0.2 кг.

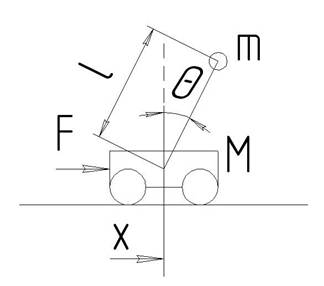
рис. 1.1. Принципиальная схема объекта управления

1.2 Математическая модель объекта управления.

Примем следующие допущения:

·  Массы считаем сосредоточенными;

·  Отсутствует трение;

·  Отсутствует сопротивление воздуха;

Составим уравнение баланса моментов на маятник и сил действующих на каретку.

Момент инерции для вращательного движения 

Баланс сил действующих на каретку:

Начальные условия: 

Решение нелинейных дифференциальных уравнений редко удается получить аналитически, т.е  нельзя получить выражения например такие:

 

Поэтому единственным средством анализа поведения остается чистое интегрирование,  автоматизированное с помощью компьютерного моделирования.

1.3 Дифференциальные уравнения в форме Коши.

Запись дифференциальных уравнений в форме Коши упрощается, если исходные уравнения разрешимы относительно старших производных,  поэтому разрешим исходные уравнения относительно   Заметим, что в исходные уравнения переменные    входят линейно и запишем уравнения в матричной форме:

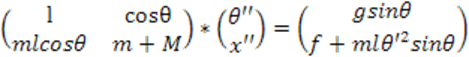
Система имеет решение, если ее определитель не тождественен нулю.

По правилу Крамера получим:

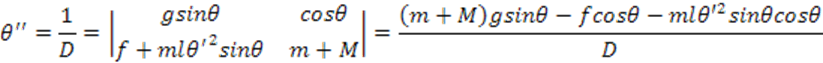
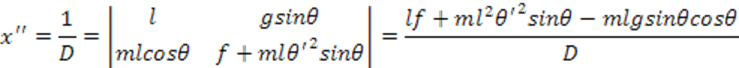
Уравнения в форме Коши:

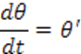
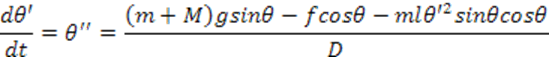
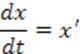
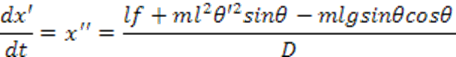
1.4  Линеаризация дифференциальных уравнений объекта управления.

Будем рассматривать малые отклонения переменных  Тогда мы можем написать, что   

Запишем линеаризованные уравнения в форме Коши:

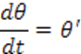
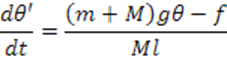
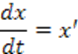
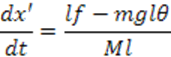
Запишем систему линейных уравнений в матричной форме пространства состояний:

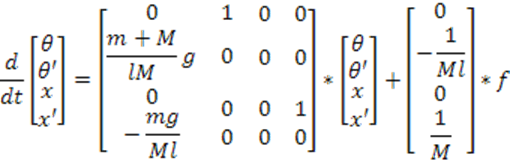
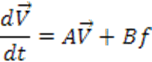
2. АНАЛИЗ ОБЪЕКТА УПРАВЛЕНИЯ.

                   2.1 Компьютерная имитация объекта управления.

Воспользуемся программой Simulink, кодирование на языке графического редактора которого базируется на дифференциальных уравнениях в форме Коши.

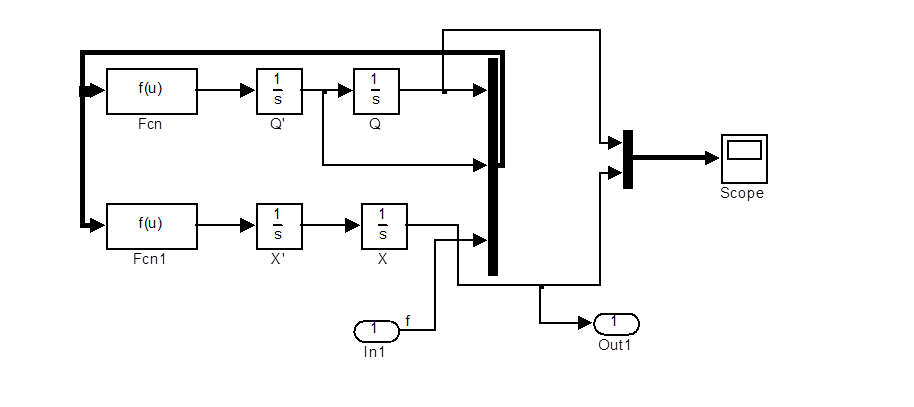
Рис.1. Компьютерная имитация объекта в среде Simulink.

Проведем исследование работы модели при различных начальных условиях:

1)

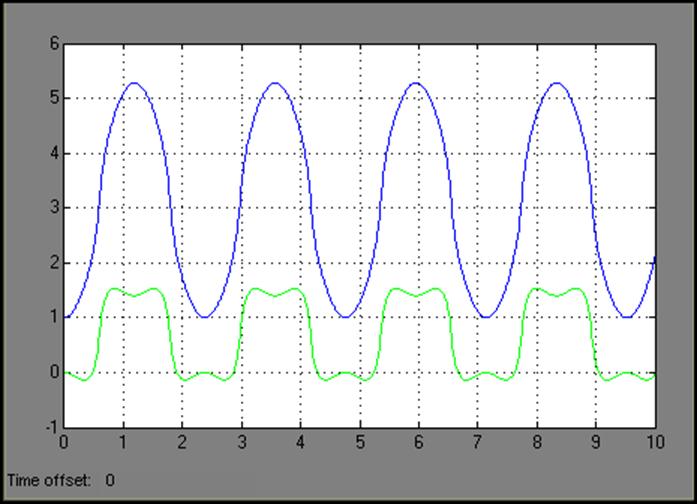
2)  

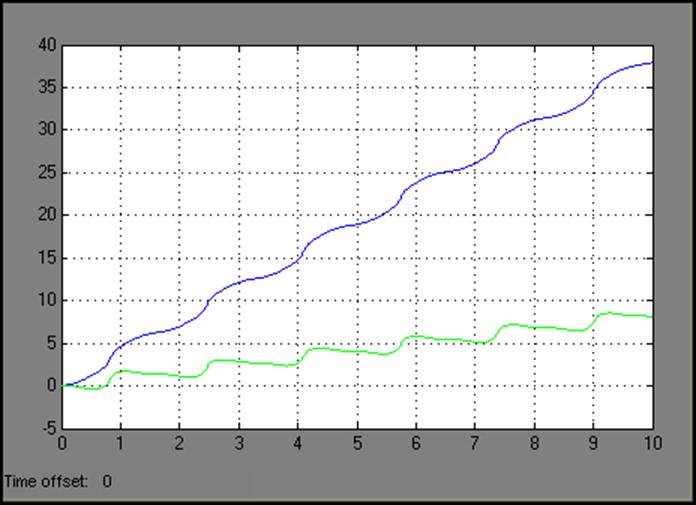
3) 

4)  

2.2 Линеаризация моделей

Для линеаризации модели объекта, при малых изменениях   воспользуемся командой:

Полученные матрицы задают линеаризованную модель в форме пространства состояний.

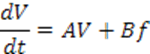
- матрицы состояний, входа (управления), выхода, обхода соответствующих размеров.

Сопоставим полученные матрицы с матрицами, полученными вручную. Можем заметить, что матрицы отличаются нумерацией переменных. Это объясняется тем, что программа компьютерной линеаризации выбирают иной порядок переменных.

По виду матриц    можно установить соответствие между компьютерными и физическими переменными   .

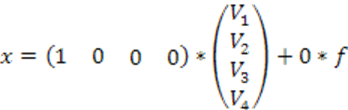
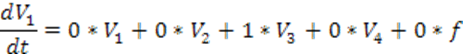
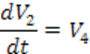
2.3 Анализ устойчивости положения равновесия  “в малом”.

Для анализа устойчивости положения равновесия воспользуемся первым методом Ляпунова, которое позволяет судить об устойчивости нелинейной системы по линеаризованным уравнениям.

Для устойчивости положения равновесия необходимо и достаточно, чтобы матрица    линеаризованной системы имела собственное значение в левой полуплоскости.

Найдем собственные значения матрицы    по команде  .

Объект неустойчив, т.к.  имеется одно правое собственное значение. Для стабилизации верхнего положения маятника необходимо создать систему автоматического регулирования.

2.4 Анализ управляемости и наблюдаемости объекта.

Задача синтеза алгоритма управления устройства (регулятора) имеет решение, если объект управляем, т.е. воздействуя на каретку силой f можем изменять все компоненты вектора состояния.

Для анализа управляемости воспользуемся критерием Калмана, который сводится к определению ранга матрицы управляемости U.

Выполним вычисления:

U=ctrb(A,B)

U =

         0    5.0000         0  245.0000

         0   -5.0000         0 -294.0000

   -5.0000         0 -294.0000         0

    5.0000         0  245.0000         0

 rank(U)

ans =

         4

Матрица имеет полный ранг (не особенная, обратимая, определитель отличен от нуля), что означает полную управляемость объекта. Наблюдаемость означает принципиальную возможность вычисления вектора состояния по измерениям положения каретки х.

Для анализа наблюдаемости воспользуемся критерием Калмана, который сводится к проверке ранга матрицы наблюдаемости.

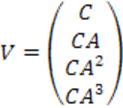
Проверим ранг:

rank(obsv(A,C))

ans =

         4

Объект наблюдаем полностью, что является необходимым условием существования решения задачи синтеза наблюдателя состояния. Объект неустойчив, но полностью управляем и наблюдаем.

2.5 Передаточная функция объекта.

Передаточная функция равна отношению изображения по Лапласу выхода объекта к его входу при нулевых начальных условиях.

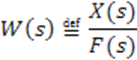
Для определения передаточной функции используем следующую команду:

[num,den]=ss2tf(A,B,C,D)