num =
0 0.0000 5.0000 -0.0000 -49.0000
den =
1.0000 -0.0000 -58.8000 0 0
Num и den – это коэффициенты числителя и знаменателя ПФ соответственно.
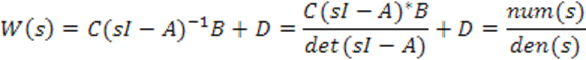
plant=tf(num,den)
Transfer function:
2.218e-014 s^3 + 5 s^2 - 1.291e-013 s - 49
------------------------------------------
s^4 - 2.665e-015 s^3 - 58.8 s^2
Ошибки вычислений привели к появлению исчезающе малых коэффициентов. Однако некоторые из них привели к завышению степени полинома числителя, что является качественной ошибкой.
Отредактируем коэффициенты полиномов вручную.
num1=[5 0 -49];
den1=[1 0 -58.8 0 0];
plant=tf(num1,den1)
Transfer function:
5 s^2 - 49
--------------
s^4 - 58.8 s^2
Приведем передаточную функцию объекта к факторизованной форме.
zpk(plant)
Zero/pole/gain:
5 (s-3.13) (s+3.13)
-----------------------
s^2 (s-7.668) (s+7.668)
Знаменатель передаточной функции представляет собой характеристический полином, корни которого в точности равны собственным значениям матрицы А.
roots(den1)
ans =
0
0
7.6681
-7.6681
3. Синтез регуляторов.
3.1 Синтез регулятора состояния.
Пусть доступна текущая информация о векторе состояния V. Тогда алгоритм формирования управляющих воздействий запишется так:
![]()
В результате охвата объекта регулятором состояния, как это изображено на рисунке 3.1, получим замкнутую систему.
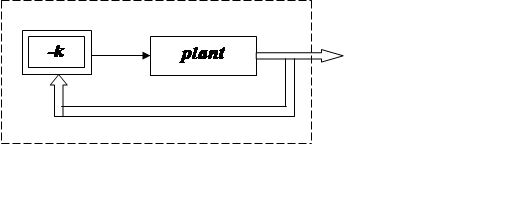
f V
Рис. 3.1 Замкнутая система с регулятором состояния
Если из уравнений системы
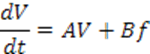
![]()
исключим переменную f , то получим дифференциальное уравнение замкнутой системы в форме пространства состояний.
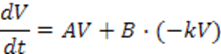
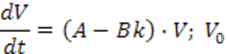
Матрица ![]() системы должна иметь желаемые
собственные значения, что обеспечивается выбором матрицы k (если пара А, В управляема).
системы должна иметь желаемые
собственные значения, что обеспечивается выбором матрицы k (если пара А, В управляема).
Для выбора матрицы k имеется два подхода:
1. Размещение собственных значений;
2. Минимизация квадратичного функционала.
Выберем первый подход и назначим желаемые собственные значения в левой полуплоскости.
Здесь есть произвол. Выберем желаемые собственные значения ориентируясь на естественную динамику объекта.
p=[-1 -2 -3 -8]';
k=place(A,B,p)
k =
-0.9796 -24.5396 -4.7184 -1.9184
3.2 Синтез наблюдателя состояния объекта.
Регулятор
состояния требует текущей информации о полном векторе состояния. Однако
непосредственно измеряется только положение каретки х. Возникает задача
вычисления в реальном времени остальных переменных ![]() . Недостаток текущей информации можно
частично скомпенсировать за счет априорной информации о модели объекта.
. Недостаток текущей информации можно
частично скомпенсировать за счет априорной информации о модели объекта.
Объект удовлетворяет необходимому и достаточному условию существования решения задачи синтеза наблюдателя – объект полностью наблюдаем.
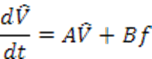
![]()
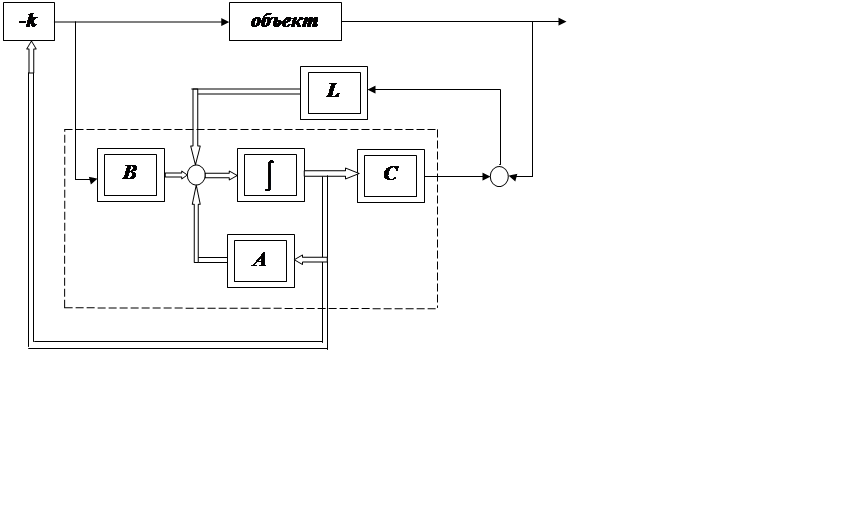
На рисунке 3.2 изображена структурная схема наблюдателя Люенберга.
Рег. Сост.
 f x
f x
δx
f ![]()
![]()
![]()
- +
ЭС
Модель объекта
Рис. 3.2 Структурная схема наблюдателя Люенберга
![]()
![]()
Наблюдатель представляет собой следящую систему, целью которой является, чтобы:
![]()
При этом состояние модели стремится к состоянию объекта.
![]()
Роль регулятора в наблюдателе играет матрица L, для поиска которой можно применить метод размещения собственных значений и использовать те же алгоритмы и программные средства, что и для синтеза регулятора состояния.
Назначим желаемые собственные значения наблюдателя в левой полуплоскости (наблюдатель должен быть устойчив), причем несколько дальше от собственных значений, назначенных при синтезе регулятора состояния. Это обеспечивает большее быстродействие процессов наблюдателя.
Матрицу L получим по команде:
p0=[-10 -12 -14 -16]';
L=place(A',C',p0)'
L =
1.0e+003 *
0.0520
-0.2364
-1.8239
1.0628
3.3 Динамический регулятор.
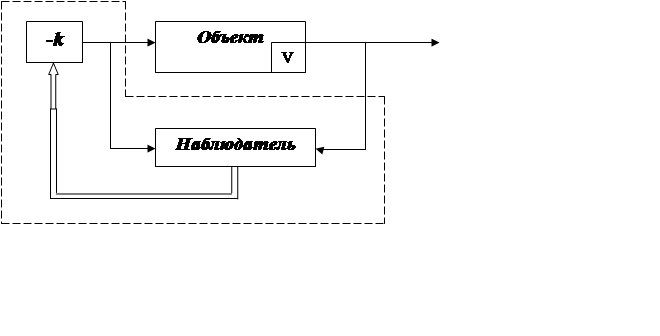
Динамический регулятор представляет собой объединение статического регулятора состояния и наблюдателя, как это показано на рисунке 3.3.
 |
f x
![]()
Динамический регулятор
Рис. 3.3 Структурная схема системы с динамическим регулятором
В результате получилась система с отрицательной обратной связью, как это показано на рисунке 3.4, где:
plant=ss(A,B,C,D);
[Ar,Br,Cr,Dr]=reg(A,B,C,D,k,L);
regulator=ss(Ar,Br,Cr,Dr);
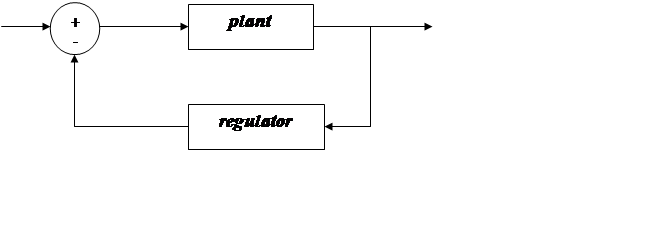 |
Рис. 3.4 Замкнутая система с динамическим регулятором
Проведем анализ устойчивости замкнутой системы с динамическим регулятором (см. рис. 3.4):
sys=feedback(plant,regulator);
eig(sys)
ans =
-16.0000
-1.0000
-2.0000
-3.0000
-14.0000
-12.0000
-10.0000
-8.0000
Полученная замкнутая система имеет в точности заданные собственные значения.
3.4 Компьютерное моделирование системы «Нелинейный объект + линейный регулятор».
Единственным способом анализа сложных нелинейных моделей оказывается компьютерное моделирование.
Отредактируем модель объекта на языке программы MATLAB/Simulink, добавив динамический регулятор, как это показано на риунке 3.5.
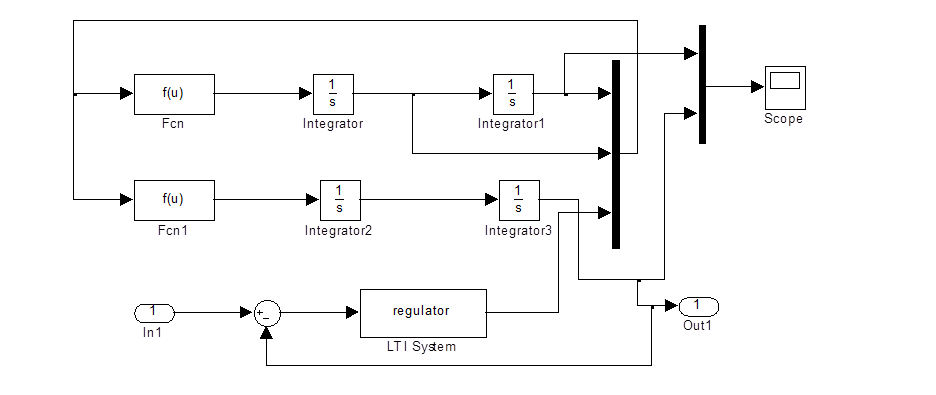
Рис. 3.5 Система с динамическим регулятором
Динамический регулятор был синтезирован в предположении о малых отклонениях переменных от положения равновесия. Поэтому компьютерные эксперименты с заданной системой проводим для малых отклонений, т.е. в малых начальных условиях на интеграторах.
Целью компьютерных
экспериментов является оценка области притяжения положения равновесия –
определение максимальных отклонений ![]() маятника и
маятника и ![]() каретки, при которых процесс
затухает.
каретки, при которых процесс
затухает.
На рисунке 3.6 изображены переходные процессы при максимальном отклонении маятника, а на рисунке 3.7 переходные процессы при максимальном отклонении каретки.
![]()
![]()
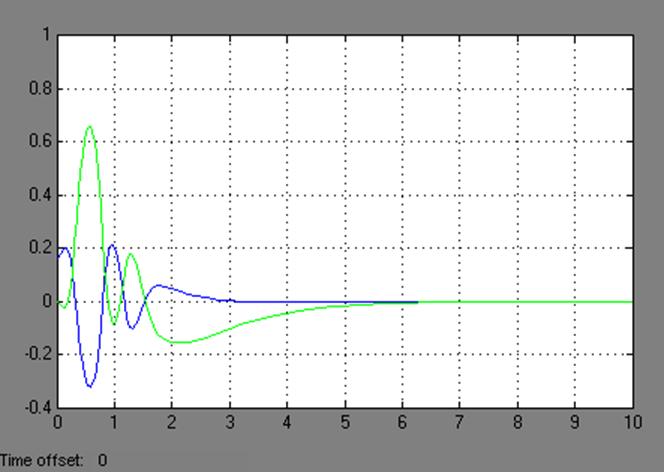
Рис. 3.6 Переходные процессы при максимальном отклонении маятника
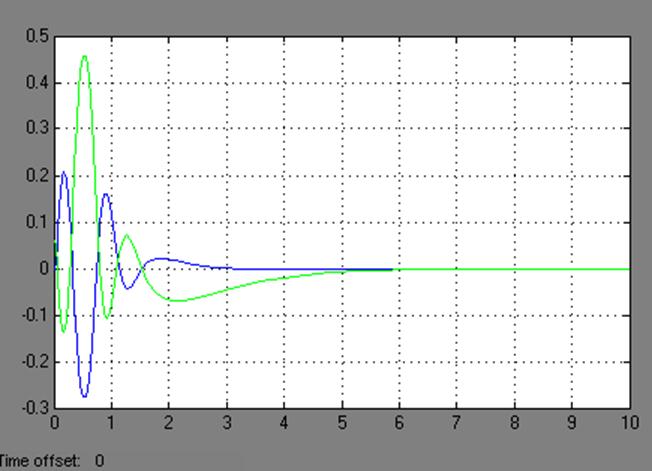
Рис. 3.7 Переходные процессы при максимальном отклонении каретки
3.5 Попытка расширения области притяжения положения равновесия.
Воспользуемся
произволом в выборе желаемых собственных значений ![]() и
и ![]() для синтеза новых регуляторов:
для синтеза новых регуляторов:
1 – более быстрого;
2 – менее быстрого;
1. Увеличим собственные значения в два раза. На рисунках 3.8 и 3.9 показаны графики переходных процессов при максимальных отклонениях маятника и каретки соответственно.
p=2*p;
k=place(A,B,p);
p0=2*p0;
L=place(A',C',p0)';
[Ar,Br,Cr,Dr]=reg(A,B,C,D,k,L);
regulator=ss(Ar,Br,Cr,Dr);
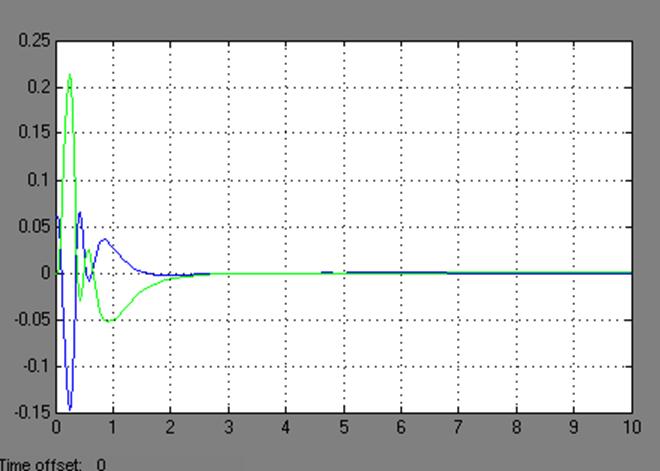
Рис. 3.8 Переходные процессы при максимальном отклонении маятника
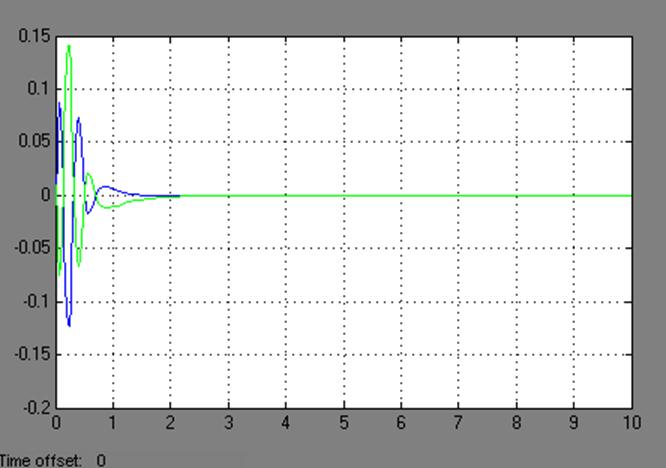
Рис. 3.9 Переходные процессы при максимальном отклонении каретки
![]()
![]()
2. Уменьшим собственные значения в два раза.
p=p/2/2;
k=place(A,B,p);
p0=p0/2/2;
L=place(A',C',p0)';
[Ar,Br,Cr,Dr]=reg(A,B,C,D,k,L);
regulator=ss(Ar,Br,Cr,Dr);
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.