Синтез замкнутой системы автоматического управления – привода робототехнической системы (гидравлического распределителя), страница 4

Оценим статическую ошибку системы.

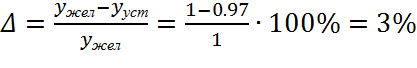                                           (7.2)

Т.о. статическая ошибка системы не превышает допустимого значения.

Оценим перерегулирование системы.

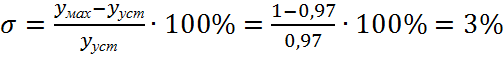                                  (7.3)

Т.о. перерегулирование системы удовлетворяет требованиям Т.З.

Проведем анализ помехозащищенности системы методом коэффициентов ошибок для расчета ошибки от действия постоянной составляющей момента.

Определим расположение частоты гармонической помехи относительно частоты среза. Частота помехи известна из задания к работе.

Найдем передаточную функцию системы по ошибке:

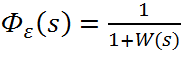                                                                     (7.4)

Т.о. получим:

   

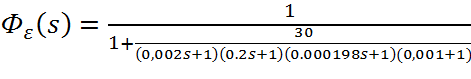
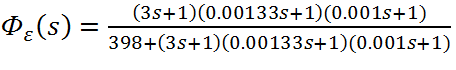                                      (7.5)

Для определения статической ошибки, рассчитаем коэффициент

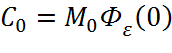                                                                       (7.6)

Получим:

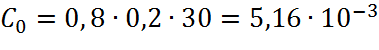                                               (7.7)

Оценим спектральную плотность помехи:

Спектральная плотность помехи в виде периодического сигнала имеет вид двух δ – функций, расположенных симметрично относительно начала координат.

 

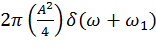
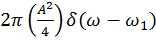
    -ω₁       0          ω₁

Будем рассматривать спектральную плотность только в области положительных частот. Тогда получим:

                                                     (7.8)

Определим спектральную плотность помехи:

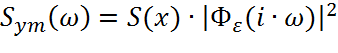                                                    (7.9)

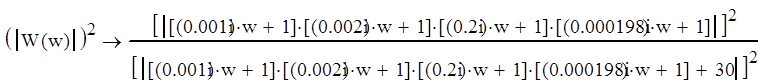
Дисперсию определим интегрируя  по всем частотам

Используя фильтрующее свойство δ функции, получим

Среднеквадратичная ошибка равна

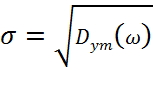
Тогда суммарная ошибка системы равна сумме ошибки от действия постоянной составляющей момента и 3 СКО. Получим:

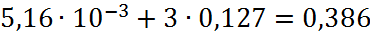
8.  Найдём конструкционное решение корректирующего устройства.

Реализацией передаточной функции W(s)=30 является усилитель мощности, выполненный на основе операционного усилителя. Т.к. свойства схем на ОУ определяются видом ОС и не зависят от типа самого ОУ, то рассчитаем только параметры обратной связи:

Рассчитаем параметры ОС для неинвертирующего усилителя:

            

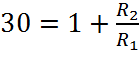
Примем R₁=100 Ом.             

Определим значение R₂

Реализацией передаточной функции 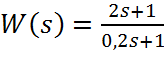 будет являться пассивный четырёхполюсник следующего вида:

Для расчета параметров элементов зададимся значением

R₁ рассчитаем из условия:

 

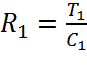
Отсюда:

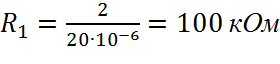
R₂ рассчитаем из условия:

 

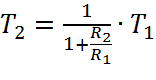
Отсюда:

R₂=900 кОм.

Окончательный вид корректирующего устройства:

Найдём дискретную передаточную функцию корректирующего устройства

1.  Рассчитаем частоту опроса для корректирующего устройства в дискретном исполнении.

Расчет проведём, исходя из правила, что время опроса (T_O) должно быть как минимум в три раза меньше минимальной постоянной времени в непрерывной части системы.

Примем T_O=0,00005 с                                        

Для нахождения передаточной функции по её непрерывному виду, проведём преобразование:

            s=jω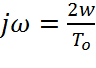                        

 

           

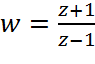
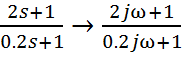
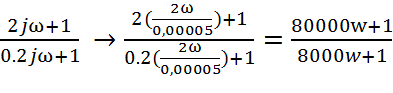
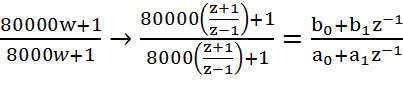  , где

Исходя из того, что 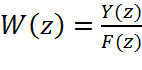. Т.е передаточная функция есть отношение выходного сигнала ко входному, получим:

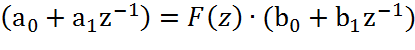
Следовательно

 

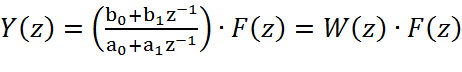
Т.о. дискретная передаточная функция КУ в общем виде будет иметь следующий вид:

 

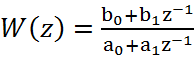
Из передаточной функции следует разностное уравнение корректирующего устройства:

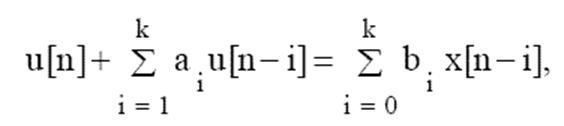
 , где

  

Алгоритм работы КУ:

 

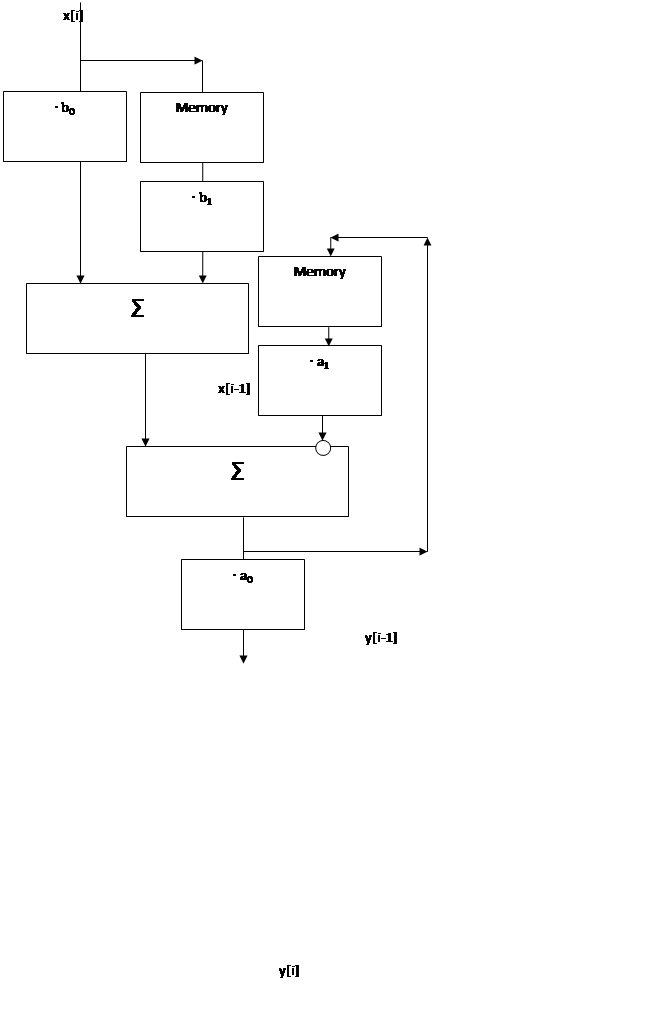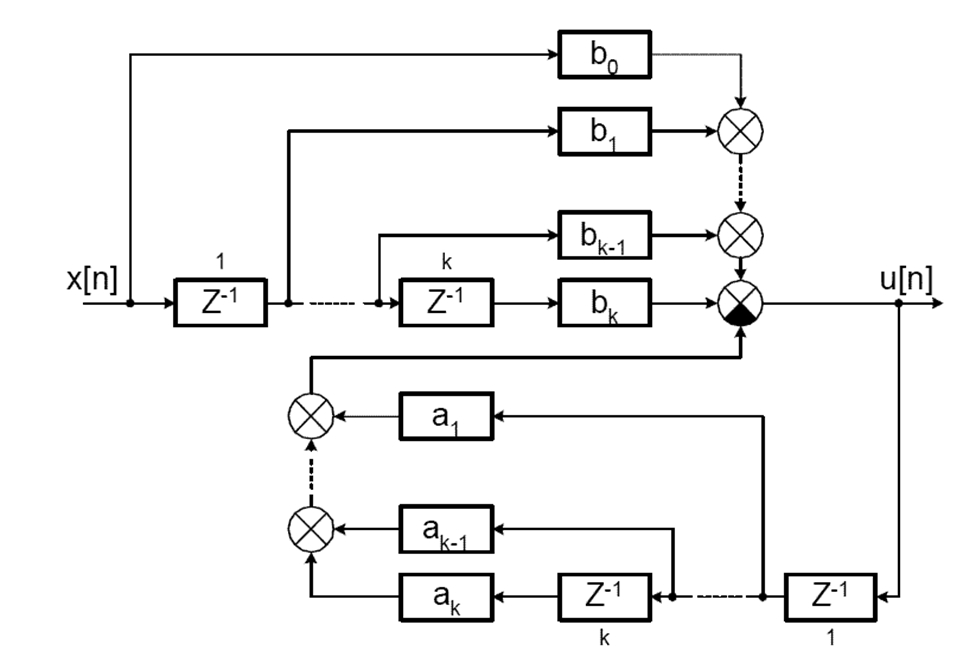
Структурная схема программной реализации решения разностного уравнения приведена ниже. Она соответствует прямому программированию.  Для аппаратной реализации прямой схемы цифрового фильтра

требуется 2k линий задержки.

Оценим момент трогания спроектированной системы, а также точность и быстродействие при действии возмущений и нелинейных факторов

Проведём анализ динамических характеристик синтезированной системы в сравнении с требованиями ТЗ при действии внешних возмущений. В качестве нелинейного возмущающего воздействия используем гармонический синусоидальный сигнал.

Возмущающее воздействие, согласно заданию:

A_s²=0.1

ω_s=100 Hz

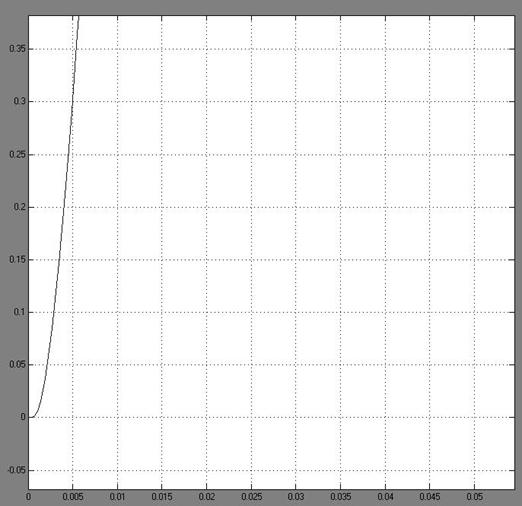
По графику оценим:

Время регулирования:

t_P=0.02 c.

Перерегулирование:

     

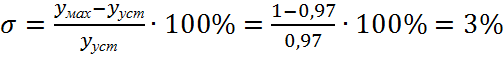
Статическую ошибку:

       

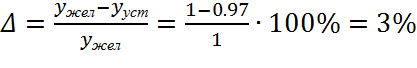
Момент трогания системы при действии возмущений составляет около 0,001 с.

Вывод: полученная система при действии внешних возмущающих воздействий заданной величины удовлетворяет требованиям Т.З.

Список литературы

1.  Бесекерский В.А. , Попов Е.В. «Теория систем автоматического регулирования», «Наука» Москва, 1975;

2.  Топчеев Ю.И., Цыпляков А.П. Задачник по теории автоматического регулирования. Учеб. пособ. Для вузов. – М.: машиностроение, 1977;

3.  Микропроцессорные системы автоматического управления / В.А. Бесекерский, Н.Б. Эфимов и др. под ред. В.А. Бесекерского. – Л.: Машиностроение, 1988;

4.  Тюкин В.Н. Теория управления, часть 2 Особые линейные и нелинейные системы, Вологда, 2000.