Регулирование температурного режима теплицы за счет автоматизации проветривания

ЗАДАНИЕ

Задание 1. Анализ линейной СУ

По заданной принципиальной функциональной схеме получить структурную функциональную схему.  По структурной схеме системы управления (СУ) построить АЧХ разомкнутой и замкнутой системы. Исследовать устойчивость СУ по одному из критериев. Построить ЛАЧХ и ЛФЧХ, определить запасы устойчивости по фазе и амплитуде. Построить переходный процесс и провести анализ качества управления, определить все его показатели. При неудовлетворительном качестве управления дать рекомендации по его улучшению.

Принципиальная схема регулирования температурного режима теплицы за счет автоматизации проветривания.

Основой устройства (рис. 1) является температурный датчик 1 (биметаллический или жидкостный) с управляющим золотником 2. При снижении температуры происходит включение двигателя 5 и вода из бачка 3 через золотник поступает в резервуар 4 на форточке-фрамуге 6, закрывая ее. При повышении температуры вода из резервуара-форточки выливается через золотник и форточка открывается для проветривания.

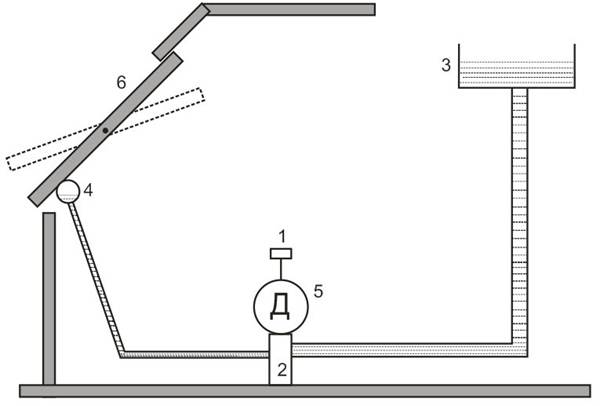
Рис. 1. Устройство для регулирования температуры в теплице

Значения:

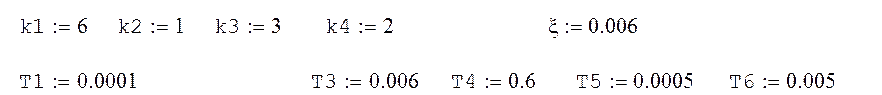
Задание 2. Анализ нелинейной СУ

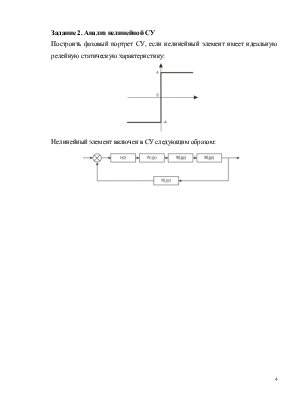
Построить фазовый портрет СУ, если нелинейный элемент имеет идеальную релейную статическую характеристику:

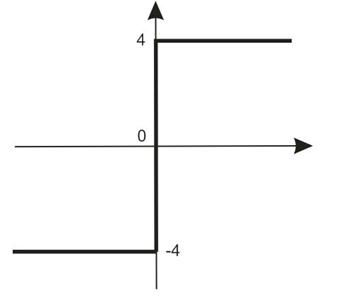
Нелинейный элемент включен в СУ следующим образом:

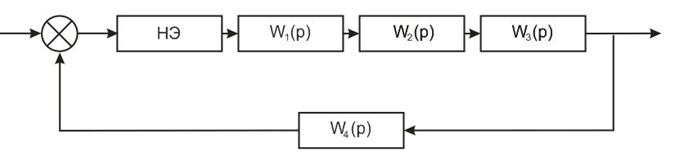
1.  Анализ линейной системы управления

1.1. Упрощение структурной схемы и нахождение передаточных функций.

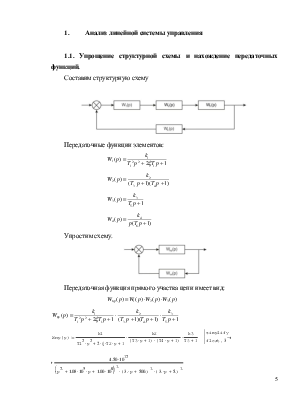
Составим структурную схему

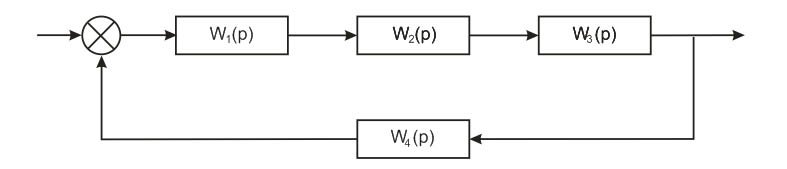
Передаточные функции элементов:

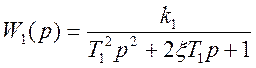
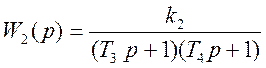
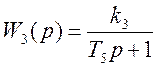
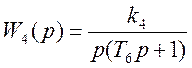
Упростим схему.

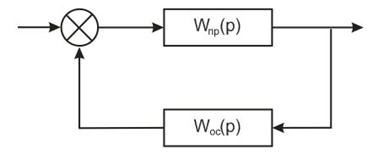
Передаточная функция прямого участка цепи имеет вид:

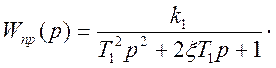
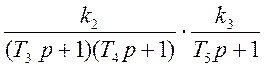
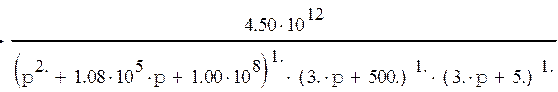
Передаточная функция обратной связи:

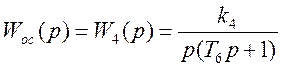
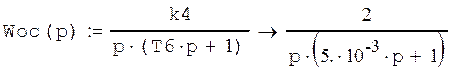
Передаточная функция замкнутой системы:

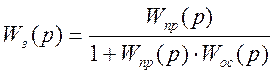
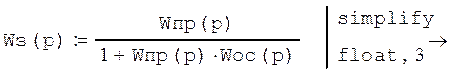
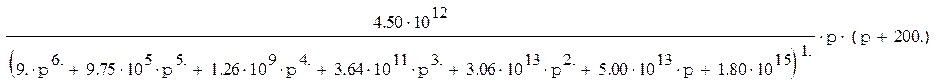
Передаточная функция разомкнутой системы:

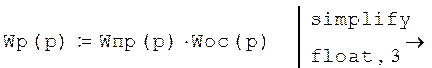
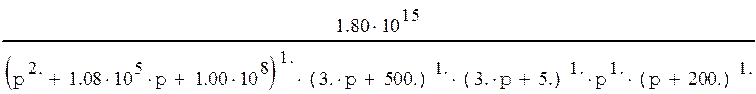
1.2.  Построение АЧХ и ФЧХ системы

Получим частотную форму записи передаточных функций.

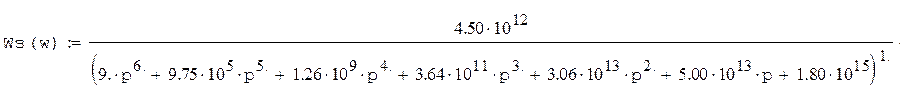
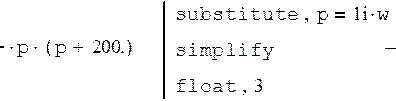
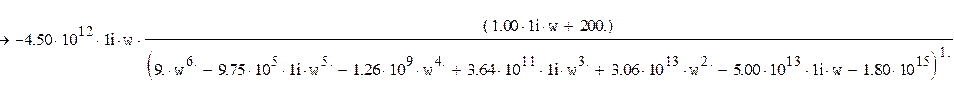
Выделим действительную и мнимую части, т.е. приведем к виду .

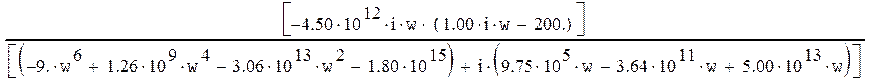
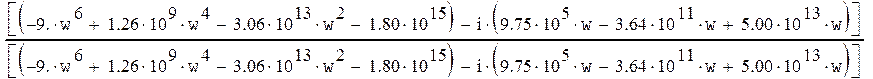Wз(w)=

=

=                                                                                                                                  =

=                                                                                                                                 +

+

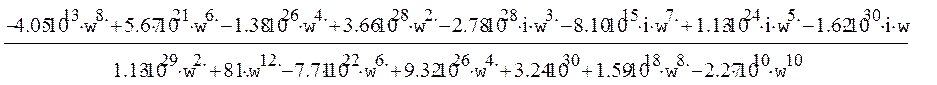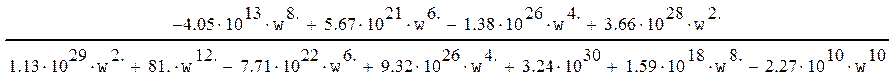
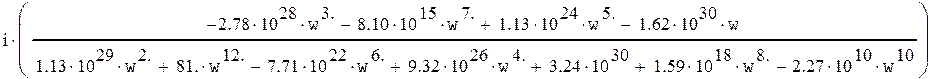
Таким образом действительная и мнимая части равны:

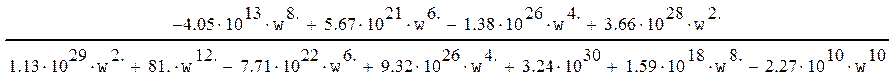
Uз(w)=

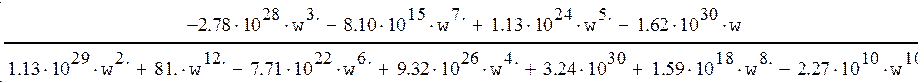
Vз(w)=

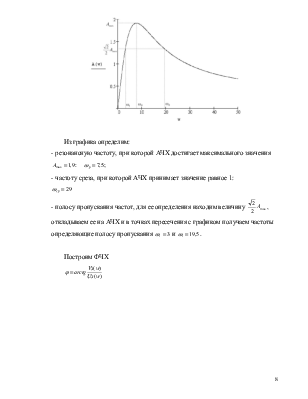
Построим АЧХ замкнутой системы.

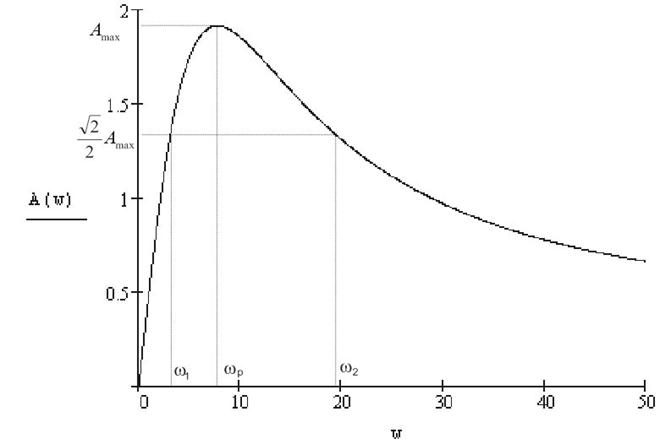
Из графика определим:

- резонансную частоту, при которой АЧХ достигает максимального значения :    ;

- частоту среза, при которой АЧХ принимает значение равное 1:

- полосу пропускания частот, для ее определения находим величину 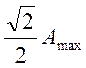, откладываем ее на АЧХ и в точках пересечения с графиком получаем частоты определяющие полосу пропускания  и .

Построим ФЧХ

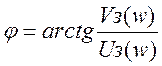
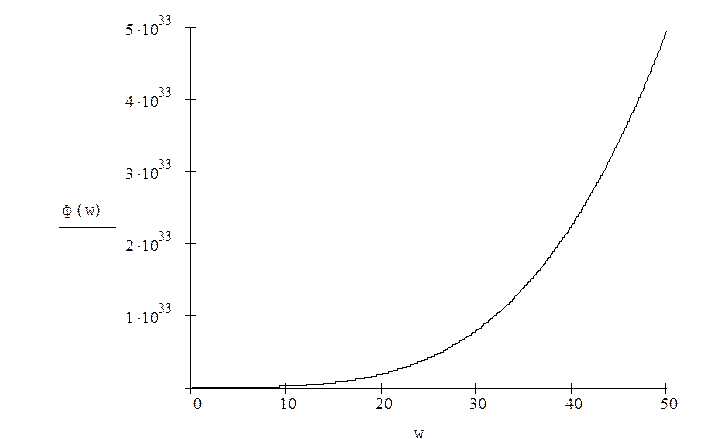
1.3.   Исследование устойчивости СУ

Проверим систему на устойчивость по критерию Ляпунова. Система устойчива, если все корни характеристического уравнения лежат в левой полуплоскости комплексной плоскости.

Найдем корни характеристического уравнения для замкнутой системы:

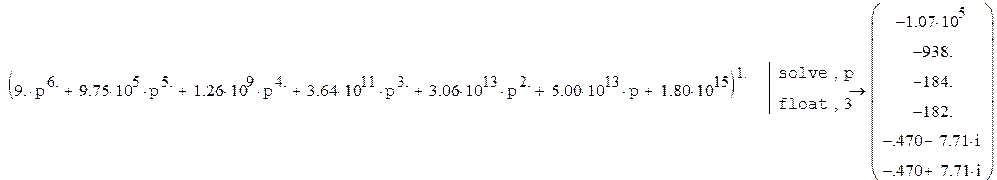Так как все вещественный части корней отрицательны, то корни характеристического уравнения находятся в левой полуплоскости комплексной плоскости, следовательно система устойчива.

1.4. Построение ЛАЧХ И ЛФЧХ и определение запасов устойчивости

Общая передаточная функция разомкнутой САУ (учитывая точку об­рыва цепи) равна передаточной функции разомкнутой системы Wр(p).

Построим систему координат в логарифмическом масштабе.

        Определяем собственную частоту каждого звена

        Колебательное                     

Инерционное звено второго порядка                       

Инерционное звено первого порядка                

Интегрирующее звено                          

Вычисляем общий коэффициент усиления

         

Строим ЛАЧХ стандартными наклонами. Поскольку система отрабатывает низкие и средние частоты, то частоты выше 1000 в рассмотрение не принимаем.

Для построения ЛФЧХ определим:

1. Колебательное звено

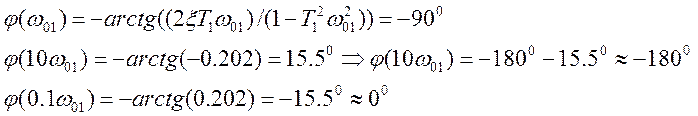
2. Апериодическое звено

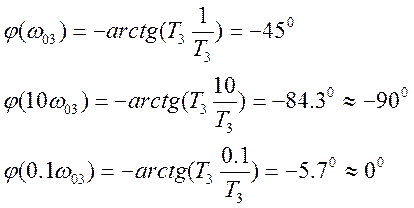
Для остальных звеньев наклоны идентичны апериодическому звену.

Строим ЛФЧХ с соответствующими стандартизованными наклонами.

Из графика определяем запасы устойчивости:

1.  Запас устойчивости по амплитуде:

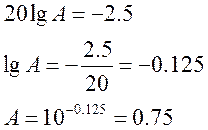
2.  Запас устойчивости по фазе составит: 

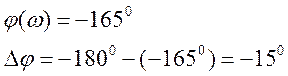
1.5. Построение переходного процесса

Определим уравнение переходного процесса:

      

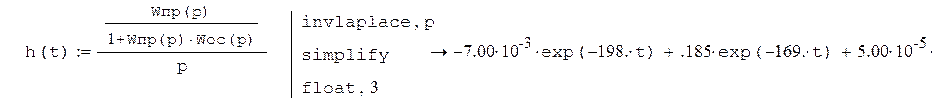
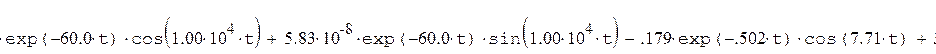
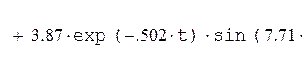
Построим график переходного процесса.

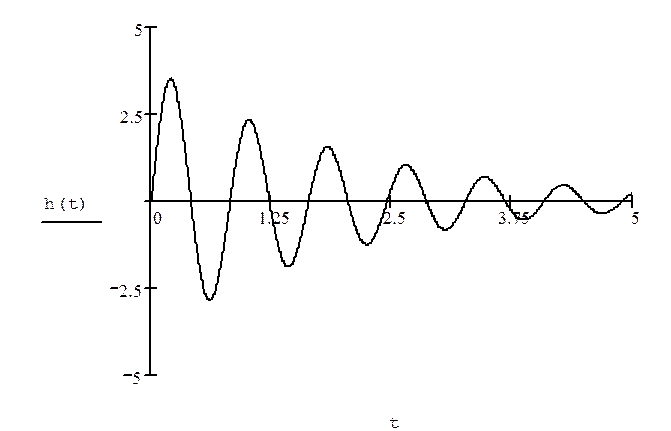
Из графика определим:

- декремент затухания:

  

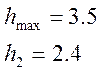
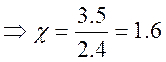
- время достижения первого максимума:

- время первого согласования:

1.6. Вывод

С учетом проведенного анализа линейной СУ можно заключить что система вполне работоспособна и выполняет функции регулирования температуры. Время регулирования неудовлетворительное для автоматики в целом, но приемлимо для конкретного примера (температура в теплице). Качество управления достаточно плохое. Коррекцию производят путем введения в СУ дополнитедьных звеньев или при помощи изменения параметров присутствующих в СУ звеньев.

2.  Анализ нелинейной системы управления

2.1. Преобразование структурной схемы

Для построения фазового портрета упростим структурную схему нелинейной СУ. Для этого выделим сгруппированные линейные элементы и нелинейный элемент.

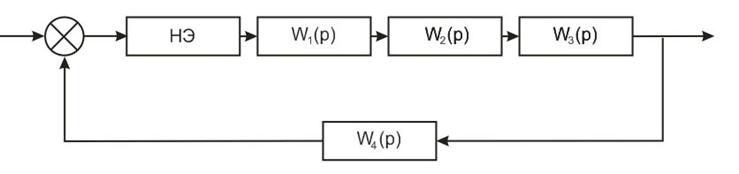
Разомкнем систему перед нелинейным элементом, перенося на новый вход системы регулирующее воздействие. Получим следующую структурную схему:

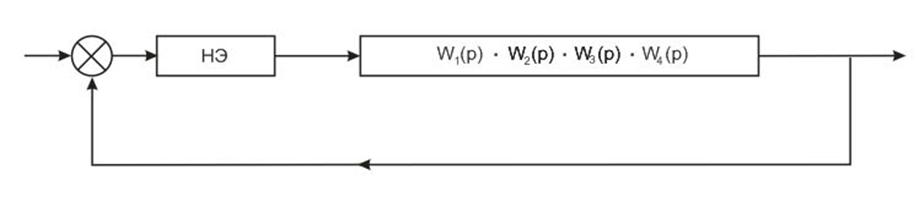
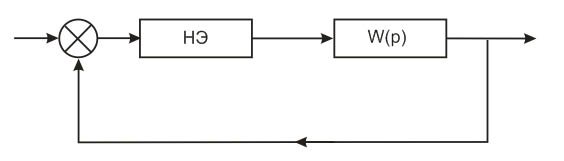
2.2. Передаточная функция линейной части

Передаточная функция линейной части равна передаточной функции разомкнутой линейной системы управления.

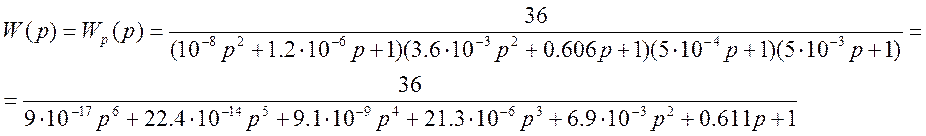
Далее, пренебрегая всеми значениями меньшими  порядка, получим следующее выражение:

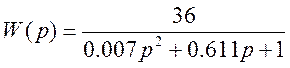
2.3 Вывод уравнений для построения фазового портрета

По определению передаточной функции:

,

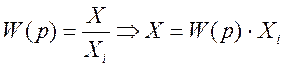получим:

Будем считать, что на вход системы подано постоянное воздействие, тогда перейдем от самих величин к их отклонениям относительно постоянного входного воздействия.

Введем обозначения:

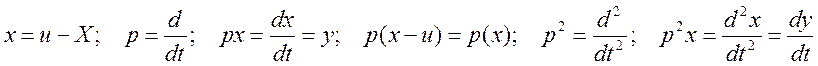
Получим дифференциальное уравнение фазовой траектории:

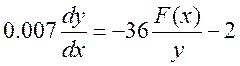
Решение данного уравнения будет строиться исходя из заданной нелинейности. Нелинейной частью системы является идеальное реле.

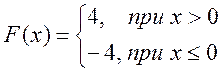
В соответствии с этим запишем дифференциальные уравнения для каждого участка:

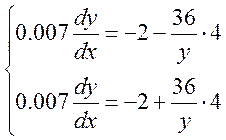
2.4. Построение фазового портрета

Пусть в начальный момент времени система выведена в точку  с координатами . Проинтегрируем вышеприведенные выражения от  до  и от  до .

Найдем решение каждого из уравнений системы.

В первом уравнении разделим переменные и проинтегрируем уравнение в общем виде:

,

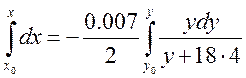получим:

.

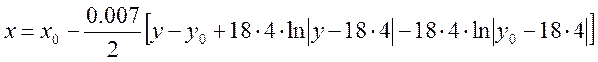Аналогично для второго уравнения:

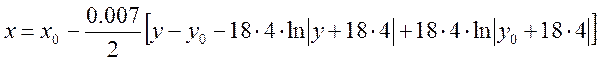
Задаваясь различными значениями y построим фазовый портрет системы. Начальные условия для первой кривой (-0,46; 0), далее конечные условия предыдущей являются начальными для следующей.

Первая кривая:

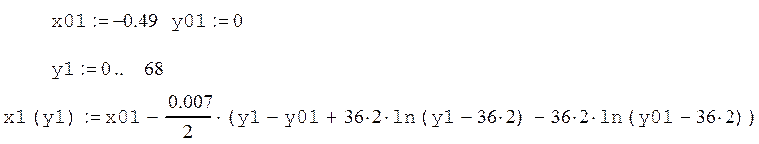
Вторая кривая:

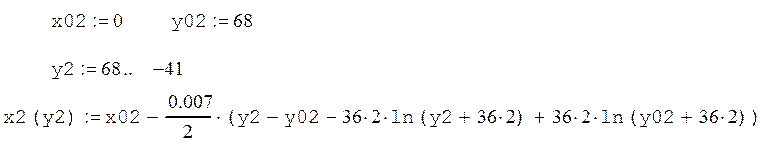
Третья кривая:

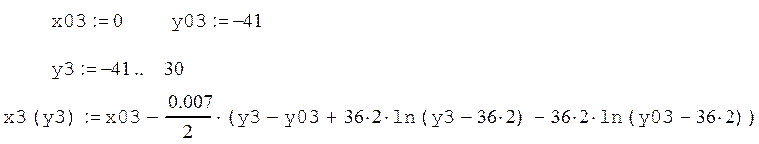
Четвертая кривая:

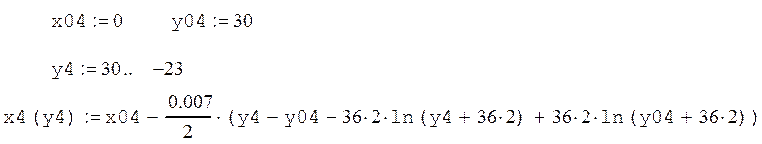
Пятая кривая:

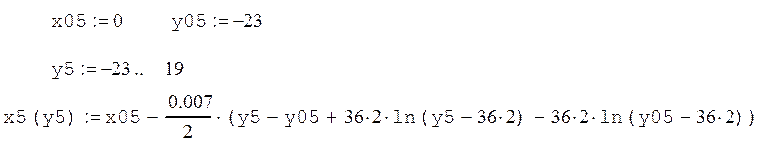
Шестая кривая:

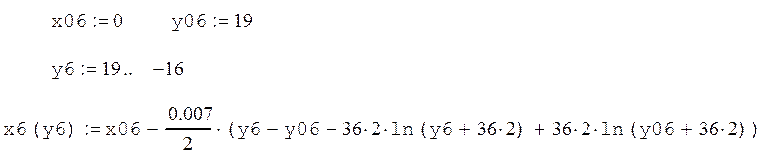
Седьмая кривая:

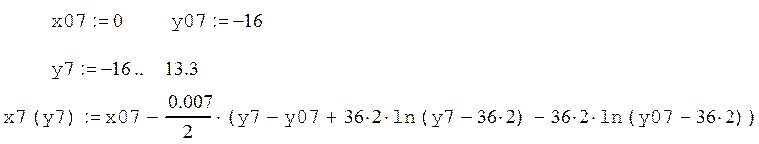
Восьмая кривая:

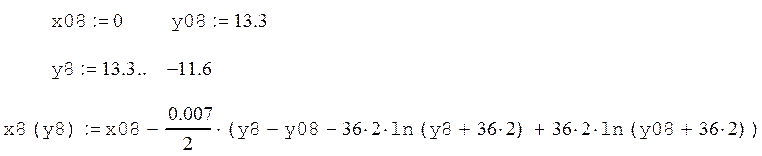
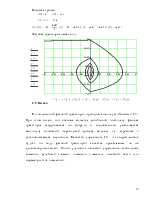
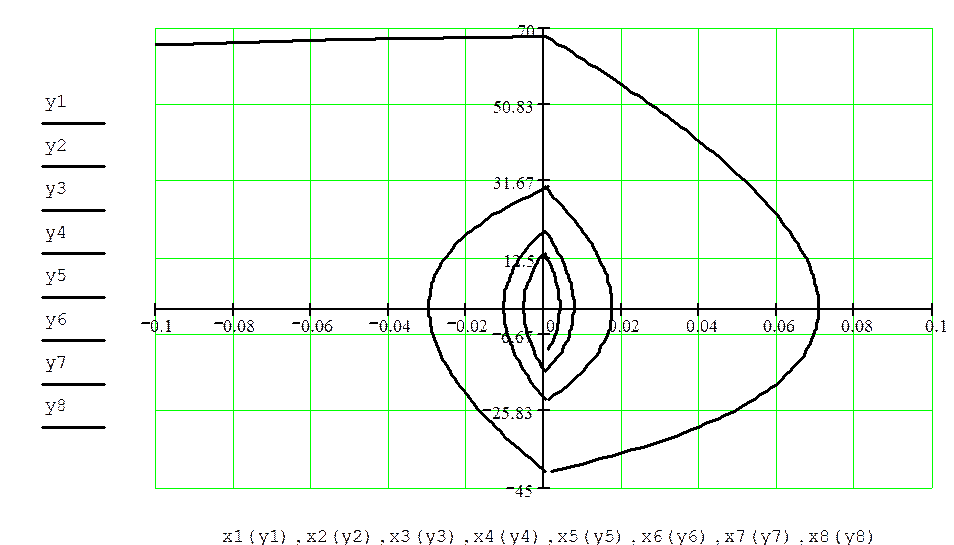
Фазовая траектория имеет вид:

2.5. Вывод

По полученной фазовой траектории проводим анализ устойчивости СУ. При этом видно, что система является устойчивой, поскольку фазовая траектория закручивается по спирали и, следовательно, уменьшается амплитуда колебаний, переходный процесс затухает, т.е. стремится к установившемуся состоянию. Качество управления СУ, о котором можно судить по виду фазовой траектории является приемлемым, но не удовлетворительными. Чтобы улучшить качество управления необходимо заменить релейный элемент, поменять элементы линейной части или параметры этих элементов.

Список литературы

1. Основы теории автоматического регулирования: Учебник для машиностроительных специальных вузов/ В.И. Крутов, Ф. М. Данилов, П. К. Кузьмин и др.; Под ред. В. И. Крутова. – 2-е изд., перераб. и доп. – М.: Машиностроение, 1984. - 368 с.: ил.

2. Теория автоматического управления/ Под ред. А.В. Нетушила. – М.: высшая школа, 1977. – 519 с.: ил.

3. Основы автоматического регулирования/ Под ред. В.С. Пугачева. – М.: Наука, 1974. – 720 с.: ил.

4. Самоучитель MathCad 11 Кирьянов Д.В.. – СПб.: БХВ – Петербург, 2003. – 560с

5. Кетков Ю.Л., Кетков А.Ю., Шульц М.М. MATLAB 6.х.: Программирование численных методов. – СПб.: БХВ-Петербург, 2004. – 672 с.: ил.

6. Исследование САУ на фазовой плоскости: Методические указания к лабораторной работе по курсу «Теория автоматического управления», Балаково 2004