эффективный коэффициент концентрации напряжения при кручении kτ=1.9 [3, т. 13.2].
5.2.14 Масштабные факторы для вала d=95 мм [из п. 5.2.2]:
масштабные факторы для нормальных напряжений εσ=0.59 [3, т. 13.3];
масштабные факторы для касательных напряжений ετ=0.59 [3, т. 13.3];
5.2.15 Коэффициенты, учитывающие влияние постоянной составляющей цикла на усталостную прочность, для легированных сталей: ψσ=0.25 [3, т. 13.4]; ψτ=0.15 [3, т. 13.].
5.2.16
Коэффициент запаса прочности по нормальным напряжениям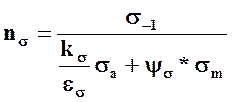 
(28)
Обозначения: nσ-коэффициент запаса прочности по нормальным напряжениям; σ-1-предел выносливости материала вала при симметричных циклах изгиба; kσ- эффективный коэффициент концентрации напряжения при изгибе; εσ- масштабные факторы для нормальных напряжений; σa-амплитуда напряжения циклов нормального напряжения; ψσ- коэффициент, учитывающий влияние постоянной составляющей цикла на усталостную прочность, для легированных сталей; σm-среднее напряжение циклов нормального напряжения.
Определим данные: σ-1=438 МПа [из п. 5.2.10]; kσ=2 [3, т. 13.2]; εσ=0.59 [3, т. 13.3]; σа= =18.49 Н/мм2 [из п. 5.2.11]; ψσ=0.25 [3, т. 13.4]; σm=0 [примечание к 3, ф. 13.27].
Подставим данные в (28)
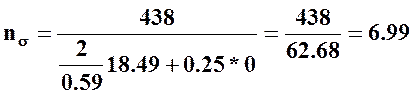
5.2.17 Коэффициент запаса прочности по касательным напряжениям
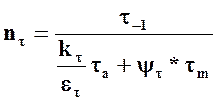(29)
Обозначения: nτ-коэффициент запаса прочности по касательным напряжениям; τ-1-предел выносливости материала вала при симметричных циклах кручения; kτ- эффективный коэффициент концентрации напряжения при кручении; ετ- масштабные факторы для касательных напряжений; τa-амплитуда напряжения циклов касательного напряжения; ψτ- коэффициент, учитывающий влияние постоянной составляющей цикла на усталостную прочность, для легированных сталей; τm-среднее напряжение циклов касательного напряжения.
Определим данные: τ-1=254.04 МПа [из п. 5.2.10]; kτ=1.9 [3, т. 13.2]; ετ=0.59 [3, т. 13.3]; τа=4.3 Н/мм2 [из п. 5.2.12]; ψτ=0.15 [3, т. 13.]; τm=4.3 Н/мм2 [из п. 5.2.12].
Подставим данные в (29)
5.2.18 Общий коэффициент запаса прочности
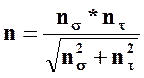≥[n](30)
Обозначения: n-общий коэффициент запаса прочности; nσ-коэффициент запаса прочности по нормальным напряжениям; nτ-коэффициент запаса прочности по касательным напряжениям; [n]-требуемый коэффициент запаса прочности.
Определим данные: nσ=6.99 [из п. 5.2.16]; nτ =17.53 [из п. 5.2.17]; [n]=1.3…1.5 [примечание к 3, ф. 13.21]- требуемый коэффициент запаса для обеспечения прочности; [n]=2.5…4 [примечание к 3, ф. 13.21] - требуемый коэффициент запаса для обеспечения жесткости.
Подставим
данные в (30)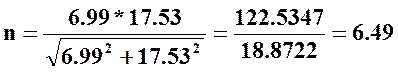 
>4
Таким образом, и прочность и жесткость обеспечены.
5.2.19 Проверка при двукратных перегрузках.
Максимальные напряжения при двукратных перегрузках:
наибольшее нормальное напряжение при передаче валом пикового момента:
σmax=2*σа=2*18.49=36.98 Н/мм2, где σa-амплитуда напряжения циклов нормального напряжения [из п. 5.2.11];
наибольшее касательное напряжение при передаче валом пикового момента:
τmax=2*τа=2*4.3=8.6 Н/мм2, где τa-амплитуда напряжения циклов касательного напряжения [из п. 5.2.12];
Коэффициент запаса по сопротивлению пластическим деформациям:
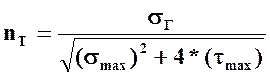≥[nТ] (31)
Обозначения: nТ-коэффициент запаса по текучести; σГ-предел текучести; [nТ]-требуемый коэффициент запаса прочности по текучести.
Определим данные: σГ=790 МПа [3, т. 10.6]; [nТ]=1.3…1.5 [примечание к 3, ф. 13.29]
Подставим
значения в (31)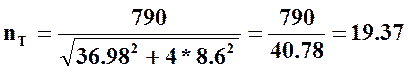 
>1.5
Этот коэффициент запаса также достаточен.
5.3 Расчет соединения червячного колеса с валом
Соединение является шпоночным
Шпонка
рассчитывается на прочность при смятии: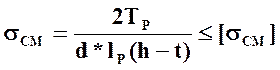 
,
где
lР=lШ-b и lШ=lП.М.-10мм, а TP=kP*T3
Обозначения: σСМ-напряжение при смятии; d-диаметр вала; lР-рабочая длина шпонки; h-высота кулачка; t-глубина паза в валу; lШ-длина шпонки; lП.М-длина полумуфты; [σСМ]-допускаемое напряжение при смятии; TP-расчетный крутящий момент; T3-крутящий момент на ведомом валу червячного редуктора.
Определим данные: d=dПЧК=95 мм [из п. 5.2.2]; lП.М.=LCT2 =171 мм [из п. 5.2.3]; h=16 мм [3, т. 4.1.]; [σСМ]=60…100 МПа [из лек.]; kp=1.5 [1, т. 17.1]; b=28 м [3, т. 4.1]; t=10 мм [3, т. 4.1]; Т3=1359 Н∙м [из п. 1.1.7];.
Определим радиус закругления шпонки: r=b/2=28 мм/2=14 мм
Обозначения: r-радиус закругления шпонки.
Подставим значения: lШ=171-10мм=161 мм, назначим по ГОСТ lШ=140 мм [примечание к [3, т. 4.1]].
Рабочая длина шпонки: lР=lШ-b=140-28=112 мм; TP=kP*T1=1.5*1359=2038.5 Н*м
и тогда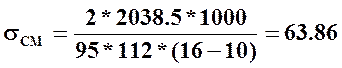 
МПа < 100 МПа
Найденное значение меньше допустимого.
5.4 Расчет соединения зубчатого колеса с валом
Соединение является шпоночным
Шпонка
рассчитывается на прочность при смятии: ,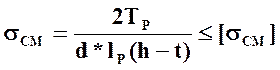
где
lР=lШ-b и lШ=lП.М.-10мм, а TP=kP*T3
Обозначения: σСМ-напряжение при смятии; d-диаметр вала; lР-рабочая длина шпонки; h-высота кулачка; t-глубина паза в валу; lШ-длина шпонки; lП.М-длина полумуфты; [σСМ]-допускаемое напряжение при смятии; TP-расчетный крутящий момент; T3-крутящий момент на ведомом валу червячного редуктора.
Определим данные: d=dПЗК=80 мм [из п. 5.2.2].; lП.М.=LCT2 =120 мм [из п. 5.2.3]; h=20 мм [3, т. 4.2]; [σСМ]=60…100 МПа [из лек.]; kp=1.5 [1, т. 17.1]; b=22 м [3, т. 4.2]; t=12м [3, т. 4.2]; Т3=1359 Н∙м [из п. 1.1.7].
Определим радиус закругления шпонки: r=b/2=22 мм/2=11 мм
Обозначения: r-радиус закругления шпонки.
Подставим значения: lШ=120-10мм=110 мм, примем по ГОСТ lШ=100 мм [примечание к [3, т. 4.1]].
Рабочая длина шпонки: lР=lШ-b=100-22=78 мм; TP=kP*T1=1.5*1359=2038.5 Н*м
и тогд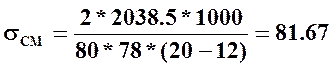а 
МПа <
100 МПа
Найденное значение меньше допустимого.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1 Кузьмин А.В. и др. Расчеты деталей машин. – Мн.: Высш. шк., 1986. – 400 с.
2 Анурьев В.И. Справочник конструктора машиностроителя. Кн. 2 – М.: Машиностроение, 1986. – 576 с.
3 Чернин И.М. и др. Расчеты деталей машин. – Мн.: Высш. шк., 1974. – 592 с.
4 Чернилевский Д.В. Курсовое проектирование машин и механизмов. – М.: Высш. школа, 1980. – 238 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.