Расчет привода технической системы и открытой зубчатой передачи, страница 3

Определим данные: K_a=49.5 [из лек.]; U=4 [из п. 1.1.5]; T₄=5318 Н*м [из п. 1.1.7]; К_Нβ=1.2 [1, т. 9.11]; [σ_H]=[σ_H]_min=466 МПа [из п. 3.1.1]; ψ_ba=0.5 [1, т. 9.1].

Примечание: К_Нβ выбирался с учетом ψ_bd==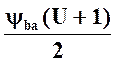

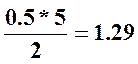
Обозначения: ψ_bd-относительная ширина колес.

Подставим известные значения в (9) 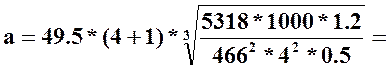381.8 мм

Округлим по ГОСТ  а=400 мм [1, т. 9.2]

            3.1.3 Назначение числа зубьев шестерни и колеса

Назначим: z₁=19 и z₂=z₁*U=19*4=76.

Обозначения: z₁-число зубьев шестерни; z₂-число зубьев колеса.

            3.1.4 Назначение угла наклона зубьев

Т.к. передача прямозубая β=0⁰-угол наклона зуба.

            3.1.5 Определение модуля зацепления передачи

Модуль зацепления определяется как 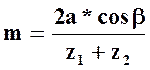==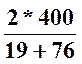8.42 мм

Округлим по ГОСТ m=9 [1, т. 9.1].

Обозначения: m-модуль зацепления; a-межцентровое расстояние; β-угол наклона зуба; z₁-число зубьев шестерни; z₂-число зубьев колеса.

            3.1.6 Определим основные размеры шестерни и колеса

Диаметр окружностей средних d=m*z

d₁=m*z₁=9*19=171 мм и d₂=m*z₂=9*76=684 мм

Диаметр окружностей выступов зубьев d_a=d+2m

d_a1=d₁+2m=171+2*9=189 мм и d_a2=d₂+2m=684+2*9=702 мм

Диаметр окружностей впадин зубьев d_f=d-2.5m

d_f1=d₁-2.5m=171-2.5*9=148.5 мм и d_f2=d₂-2.5m=684-2.5*9=661.5 мм

Ширина зубчатого венца

b₂=ψ_ba*a=0.5*400=200 мм и b₁=b₂+5мм=205 мм

Обозначения: d₁-средний делительный диаметр шестерни; d₂-средний делительный диаметр колеса; b₁-ширина зубчатого венца шестерни; b₂-ширина зубчатого венца колеса; ψ_ba-коэффициент ширины колес.

            3.1.7 Определение окружной скорости передачи

Окружная скорость находится по формуле 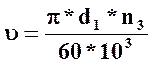=0.75 м/с

Обозначения: υ-окружная скорость; n₃-число шестерни; d₁-средний делительный диаметр шестерни.

Определим данные: d₁=171 мм [из п. 3.1.6]; n₃=84 1/мин [из п. 1.1.6].

            3.1.8 Назначение степени точности

Степень точности S=9 [1, т. 9.9], с учетом окружной скорости.

3.1.9 Расчет передачи на контактную прочность

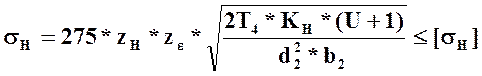(10), где K_H=K_Hα*K_Hβ*K_Hυ (11)

Обозначения: σ_Н-расчетное контактное напряжение; z_H-коэффициент формы поверхности зубьев; z_ε-коэффициент суммарной длины контактной линии; T₄-крутящий момент на ведомом валу зубчатой передачи; K_H-коэффициент нагрузки; [σ_H]-допускаемое контактное напряжение; K_Hα-коэффициент распределения нагрузки между зубьями; К_Нβ-коэффициент учитывающий распределение нагрузки по зубьям; K_Hυ-коэффициент динамичности нагрузки; d₂-средний делительный диаметр колеса; b₂-ширина зубчатого венца колеса.

Определим данные: z_H=1.77 [из лек.]; z_ε=1 [из лек.]; Т₄=5318 Н*м [из п. 1.1.7]; [σ_H]=466 МПа [из п. 3.1.2]; K_Hα=1 [из лек.]; К_Нβ=1.2 [из п. 3.1.2]; K_Hυ=1 [из лек.]; d₂=684 мм [из п. 3.1.6]; b₂=200 мм [из п. 3.1.6].

Подставим известные данные в (11)→(10) K_H=1*1*1.2=1.2

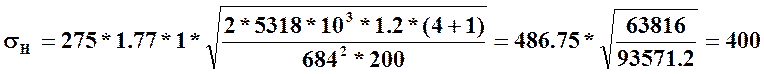 МПа < 466 МПа

Найденное значение меньше допустимого.

3.1.10 Расчет передачи на усталость зубьев при изгибе

Найдем эквивалентное число зубьев: z_υ1=z₁/cos³β=z₁=19 и z_υ2=z₂/cos³β=z₂=76

Обозначения: z_υ1-эквивалентное число зубьев шестерни; z_υ2-эквивалентное число зубьев колеса; z₁-число зубьев шестерни; z₂-число зубьев колеса; β-угол наклона зубьев;

Определим наименее прочное колесо передачи  по отношению [σ_F]/y_F

Обозначения: y_F-коэффициент формы зубьев; [σ_F]-напряжение изгиба.

Определим данные: y_F1=4.09 [1, т. 9.10]; y_F2=3.61 [1, т. 9.10]; [σ_F]₁=270 МПа [из п. 3.1.1]; [σ_F]₂=240 МПа [из п. 3.1.1].

Получим: [σ_F]₁/y_F1=270/4.09=66.015 МПа и [σ_F]₂/y_F2=240/3.61=66.482 МПа

Расчет ведем для шестерни, т.к. отношение имеет меньшее значение

Найдем расчетное напряжение изгиба: 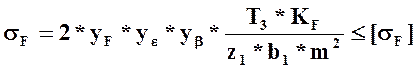 (12)

Обозначения: σ_F-расчетное напряжение изгиба; [σ_F]-допускаемое напряжение изгиба ; y_F-коэффициент формы зуба; y_ε-коэффициент перекрытия зубьев; y_β-коэффициент наклона зубьев; T₃-крутящий момент на ведомом валу червячного редуктора; К_F-коэффициент нагрузки; b₁-ширина зубчатого венца шестерни; m-модуль зацепления зубчатой передачи.

Определим данные: y_ε=1 [из лек.]; y_β=1 [из лек.]; Т_К=1359 Н*м [из п. 1.1.7]; b₁=205 мм [из п. 3.1.6]; z₁=19 [из п. 3.1.3]; m=9 [из п. 3.1.5]; [σ_F]=270 МПа [1, т. 11.6].

Определим коэффициент нагрузки К_F=K_Fα* K_Fβ*K_Fυ

Обозначения: К_F-коэффициент нагрузки; K_Fα-коэффициент распределения нагрузки между зубьями; K_Fβ-коэффициент распределения нагрузки по ширине зуба; K_Fυ-коэффициент динамичности нагрузки.

Определим данные: K_Fα=1 [из лек.]; K_Fβ=α*K_Hβ=1.15*1.2=1.38 [1, т. 9.11]; К_Нβ=1.2 [из п. 3.1.2];  K_Fυ=1.25 [1, т. 9.13].

Обозначения: α-числовой коэффициент; К_Нβ-коэффициент учитывающий распределение нагрузки по зубьям.

Т.е. К_F=1*1.38*1.25=1.725

Подставим известные значения в (12)

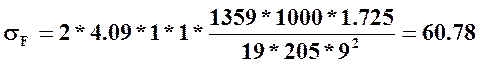МПа < 270 МПа

Найденное значение меньше допустимого.

4 КОНСТРУКТИВНЫЕ РАЗМЕРЫ ЗУБЧАТОГО КОЛЕСА.

ШЛИЦЕВОЕ СОЕДИНЕНИЕ ЗУБЧАТОГО КОЛЕСА С ВАЛОМ

            4.1.1 Определение посадочного диаметра на вал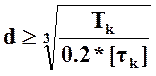

Обозначения: d-посадочный диаметр зубчатого колеса на вал; T_k-крутящий момент на ведомом зубчатом колесе; [τ_k]-пониженное допускаемое напряжение при кручении;

Определим данные: T_k=T₄=5318 Н*мм [из п. 1.1.7]; [τ_k]=25 МПа [из лек.]

Подставим значения 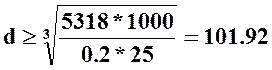мм, примем d=102 мм.

            4.1.2 Определение основных размеров

Обозначим тип исполнения колес. По диаметру окружностей выступов зубьев

d_a=702 мм [из п. 3.1.6] принимаем колеса литые со спицами.

Расчетные формулы: d_CT=1.6*d (13); L_CT=(1.2-1.5)*d (14); δ=(2.5-4)*m (15); n=0.5*m (16); H=0.8*d (17); H₁=0.8*H (18); C₁=0.2*H (19); S=0.15*H (20); e=0.8*δ (21);

Обозначения: d-посадочный диаметр зубчатого колеса на вал; d_CT-диаметр ступицы; L_CT-длина ступицы; δ-толщина зубчатого венца; m-модуль зацепления; n-ширина фаски; S-ширина спицы; С₁-толщина диска.

Определим данные: m=9 [из п. 3.1.5]; d=102 мм [из п. 4.1.1].

Подставим известные значения в (13)-(21)

d_CT=1.6*102=163.2 мм; L_CT =1.5*102=153 мм, т.к. ширина зубчатого венца b=200 мм [из п. 3.1.6], принимаем L_CT=200 мм; δ=3*9=27 мм; n=0.5*9=4.5 мм; H=0.8*102=81.6 мм; H₁=0.8*81.6=65.3 мм; C₁=0.2*81.6=16.3 мм; S=0.15*81.6=12.2 мм; e=0.8*27=21.6 мм.