Определим
посадочный диаметр зубчатого колеса на вал: dПЗК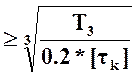
(25)
Обозначения: dПЗК-посадочный диаметр зубчатого колеса на вал; T3-крутящий момент на валу червячного колеса; [τК]-пониженное допускаемое напряжение при кручении.
Определим данные: T3=1359 Н∙м [из п. 1.1.7]; [τК]=25 МПа [из лек.]
dПЗК
≥
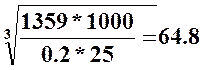примем
этот диаметр 80 мм [3, т. 13.1].
Определим диаметр вала подшипника: dП=dПЗК+7…12 мм
Обозначения: dП-диаметр вала подшипника.
Тогда dП=80+10=90 мм (кратен 5), по этому диаметру подберем подшипник средней серии, радиально-упорный однорядный [3, т. 15.7]: марка 46318, ширина подшипника B=43 мм.
Определим промежуточный диаметр вала, между подшипником и зубчатым колесом:
основное условие для этого диаметра: dПЗК<dКП<dП
Обозначения: dПЗК-посадочный диаметр зубчатого колеса на вал; dКП-промежуточный диаметр вала; dП-диаметр вала подшипника.
Согласно условию назначим dКП=85 мм.
Определим диаметр вала под червячным колесом: dПЧК=dП+5 мм
Обозначения: dПЧК-посадочный диаметр червячного колеса на вал.
Согласно условию назначим: dПЧК=95 мм.
Определим высоту заплечиков: h=8 мм [1, т.14.7].
Определим диаметр буртика: dб=dПЧК+2*h=95+2*8=111 мм
5.2.3. Определим длины участков вала
Длина участка вала под зубчатым колесом: l1=LCT1-2мм
Длина промежуточного участка вала, участок под подшипником l2=l3=l7=B
Ширина буртика l4=l6=20мм [из лек.]
Длина участка вала под червячным колесом l5=LCT2, где LCT2=1.5…1.8*dПЧК
Обозначения: LCT1-длина ступицы зубчатого колеса; LCT2-длина ступицы червячного колеса; B-ширина подшипника; dПЧК-посадочный диаметр червячного колеса на вал.
Определим данные: LCT1=1.5*dПЗК=1.5*80=120 мм [примечание к 3, рис.10.14] и dПЗК=80 мм [из п. 5.2.2]; B=43 мм [3, т. 15.7]; dПЧК=95 мм [из п. 5.2].
Тогда: l1=120-2мм=118 мм; l2=l3=l7=43 мм; l5=LCT2=1.8*95=171 мм [примечание к 3, рис.11.10];
5.2.4 Найдем участки x1, x2, x3.
x1=l1/2+l2+l3/2=118/2+43+43/2=123.5 мм;
x2=l3/2+l4+l5/2=43/2+20+171/2=127 мм;
x3= l5/2+l6+l7/2=171/2+20+43/2=127 мм;
5.2.5 Определим опорные реакции в вертикальной плоскости
ΣMC=-RA*(x3+x2) – QЧК*dЧК/2+FЧК*x2 – PЗК*x1=0
RA=(– QЧК*dЧК/2+FЧК*x2 – PЗК*x1)/(x3+x2)
ΣMA=RC*(x3+x2) – QЧК*dЧК/2+FЧК*x3 – PЗК*(x1+x2+x3)=0
RC=( QЧК*dЧК/2 – FЧК*x3+PЗК*(x1+x2+x3))/(x3+x2)
Обозначения: RA-реакция опоры в точке А; RC- реакция опоры в точке C; x1, x2, x3-длины участков вала; QЧК-осевое усилие действующее на червячное колесо; dЧК- делительный диаметр червячного колеса; FЧК-радиальное усилие действующее на червячное колесо; PЗК-окружное усилие действующее на шестерню.
Определим данные: x1=123.5 мм [из п. 5.2.4]; x2=127 мм [из п. 5.2.4]; x3=127 мм [из п. 5.2.4]; QЧК=3371.43 Н [из п. 5.2.1]; dЧК=d2=448 мм [из п. 5.1]; FЧК=2208.19 Н [из п. 5.2.1]; PЗК=15894.74 Н [из п. 5.2.1].
Найдем значения реакций:
RA=(– 3371.43*448/2+2208.19*127–15894.74*123.5)/( 127+127)=-12100.59 Н
RC=(3371.43*448/2–2208.19*127+15894.74*(123.5+127+127))/(127+127)=27995.33 Н
5.2.6 Определение изгибающих моментов в вертикальной плоскости
Mx/=-RA*x3=12100.59*127=1536.78*103 Н*мм
Mx//=RC*x2=27995.33*127=3555.41*103 Н*мм
Mx///=PЗК*x1=15894.74*123.5=2598.79*103 Н*мм
Все данные взяты из п. 5.2.5
5.2.7 Определим опорные реакции в горизонтальной плоскости
ΣMC=RA/*(x3+x2)+PЧК/*x2-FЗК/*x1=0
RA/=(-PЧК/*x2+FЗК/*x1)/(x3+x2)
ΣMA=-R/C*(x3+x2)+PЧК/*x3-FЗК/*(x1+x2+x3)=0
R/C=( PЧК/*x3-FЗК/*(x1+x2+x3))/(x3+x2)
Обозначения: R/A-реакция опоры в точке А; R/C- реакция опоры в точке C; x1, x2, x3-длины участков вала; P/ЧК-окружное усилие действующее на червячное колесо; FЗК-радиальное усилие действующее на шестерню.
Определим данные: x1=123.5 мм [из п. 5.2.4]; x2=127 мм [из п. 5.2.4]; x3=127 мм [из п. 5.2.4]; PЧК/=6066.96 Н [из п. 5.2.1]; FЗК/=5785.21 Н
Найдем значения реакций:
RA/=(-6066.96*127+5785.21*123.5)/(127+127)=690.46 Н
R/C=( 6066.96*127-5785.21*(123.5+127+127))/(127+127)=-6475.67 Н
5.2.8 Определение изгибающих моментов в горизонтальной плоскости
My/=-RA*x3=-690.46*127=-87.69*103 Н*мм
My//=FЗК/*x1=5785.21*123.5=944.73*103 Н*мм
5.2.9 Определить суммарный изгибающий момент в каждой точке
Для
точки A:
=0
Для
точки B: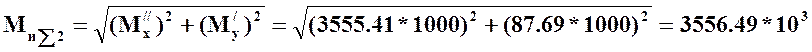
Н*мм
Для
точки C: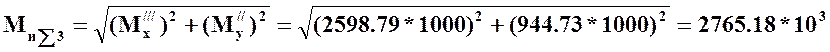
Н*мм
Для точки D:=0
Обозначение: M-изгибающий момент.
Дальнейший расчет будем
вести для точки В, т. к. точка это наиболее опасное место сечения, по изгибающему
моменту 
Н*мм.
5.2.10 Определим пределы выносливости стали 45 ХН (легированная):
при изгибе σ-1=0.35*σВ+70…120 Н/мм2=0.35*980+95=438 МПа
при кручении τ-1=0.58*σ-1=0.58*438=254.04 МПа
Обозначения: σВ-предел прочности; σ-1-предели выносливости при изгибе; τ-1-предели выносливости при изгибе.
5.2.11 Нормальные напряжения для сечения под червячным колесом
σа=σи=Т3/W
(26), где W=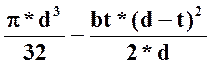
(27) [3, т. 13.2]
Обозначения: σa-амплитуда циклов нормальных напряжений; σи-амплитуда циклов нормальных напряжений в сечении; T3-крутящий момент на ведомом валу червячного редуктора; W-момент сопротивления; d-диаметр вала; b-ширина шпоночной канавки; t-глубина шпоночной канавки.
Определим данные: Т3=1359 Н∙м [из п. 1.1.7]; d=dПЧК=95 мм [из п. 5.2.2]; b=28 м[3, т.
4.1]; t=10 мм [3, т. 4.1].
Подставим
данные W=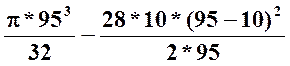
=73525.23 мм3 и
σа=σи=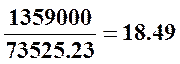
Н/мм2.
5.2.12 Касательные напряжения отнулевого цикла для сечения под колесом
τа=τm=τmax/2=T3/(2*WК),
где WК=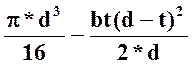
[3, т. 13.2]
Обозначения: τа-амплитуда напряжения циклов касательного напряжения; τm-среднее напряжение циклов касательного напряжения; τmax-максимальное значение напряжения циклов касательного напряжения; T3-крутящий момент на ведомом валу червячного редуктора; WК-момент сопротивления при кручении; b-ширина шпоночный канавки; t-глубина шпоночной канавки.
Определим данные: Т3=1359 Н∙м [из п. 1.1.7]; d=dПЧК=95 мм [из п. 5.2.2]; b=28 м[3, т.
4.1]; t=10 мм [3, т. 4.1].
Подставим значения: WК=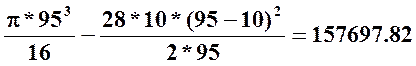
мм3 и
τа=τm=τmax/2=1359000/(2*157697.82)=4.3 Н/мм2, также τmax=2*4.3=8.6 Н/мм2
5.2.13 Эффективные коэффициенты концентраций напряжений (шпоночная канавка)
для стали 45 ХН с пределом прочности до 1000 Н*мм3:
эффективный коэффициент концентрации напряжения при изгибе kσ=2 [3, т. 13.2];
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.