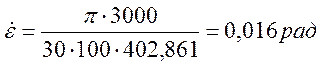Разработка системы автоматического управления промышленным оборудованием, страница 4

.

Получим коэффициент передачи системы для заданного значения

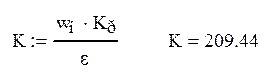
Таким образом, при заданной статической точности системы, имеем более чем двукратный запас устойчивости.

5.  Количественный анализ свойств системы в частотной области.

Рассмотрим  свойства САУ ПЭ  и  частотной  области. Построим  амплитудно-частотную (АЧХ)  и фазо-частотную  (ФЧХ)  характеристики  разомкнутой  системы при выбранном коэффициенте передачи системы. Передаточная функция разомкнутой системы определяется (22)

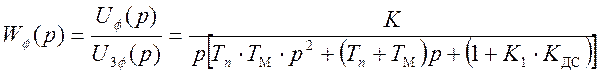                    (32)

Разделим числитель и знаменатель выражения (32) на (1+К_кр·К_ДС), подставим

численные значения параметров и преобразуем выражение в квадратных скобках к стандартному виду колебательного звена. В результате получим

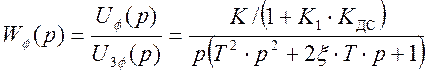                              (33)

Подставив в (33)  р = jω, получим частотную передаточную функцию

          (34)

Амплитудно-частотная характеристика (АЧХ) системы равна

                                               (35)

Фазо-частотная (ФЧХ) характеристика системы равна

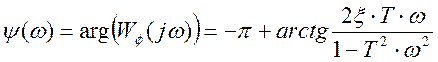                             (36)

Задаваясь значением w от 0 до ∞ получим АЧХ и ФЧХ системы

Расчёты сведём в таблицу 4.

Располагая данными  таблицы 4, получим логарифмические частотные характеристики

L(ω)=20lgA(ω),     φ(ω)=ψ(ω)                               (37)

По данным таблицы 4 построим амплитудно-фазовую частотную  характеристику (АФЧХ) системы (рисунок 5).

Таблица 4

ω, с-1	1-T2ω2	2ξTω	A(ω)	20lgA(ω)	arctg2ξTω/1-T2ω2	ψ, град
1	1	0.035	62.603	38.745	-1.592	-91.192
100	0,999	3.469	0.159	-7.615	-3.138	-179.808
199	0,997	6.903	0.025	-21.336	-3.758	-215.314
298	0.993	10,337	0.029	-30.718	-4.042	-231.591
397	0.987	13,771	0.013	-37.745	-4.199	-240.592
496	0.98	17,205	6.817e-3	-43.328	-4.298	-246.233
595	0.971	20,64	4.005e-3	-47.949	-4.365	-250.081
694	0.96	24,074	2.545e-3	-51.885	-4.413	-252.866
793	0.948	27,508	1.716e-3	-55.311	-4.450	-254.973
892	0.934	30,942	1.210e-3	-58.343	-4.479	-256.621
991	0.919	34,376	8.850e-4	-61.061	-4.502	-257.945

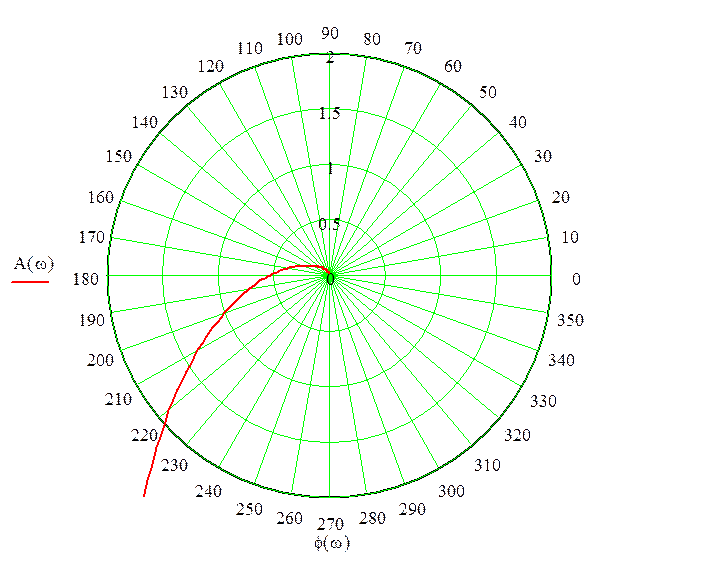
Рисунок 5. АФЧХ системы

          Согласно критерию устойчивости Найквиста, данная система является устойчивой, так как график не охватывает точку с координатами (-1;j0). АФЧХ системы при К = К_кр ,  К< К_кр , К>К_кр изображена на рисунке 6.

Рисунок 6. АФЧХ системы при различных значениях K

Как видно из рисунка 6, система находится на грани устойчивости при К = К_кр и становится неустойчивой при увеличении K. С уменьшением К, увеличиваются запасы устойчивости по фазе и амплитуде.

По данным таблицы 4 построим логарифмические частотные характеристики. Для этого по оси абсцисс откладывается частота в логарифмическом масштабе частот, а по оси ординат амплитуда в децибелах (20 lg A(ω)) и сдвиг по фазе (ψ(ω)) в градусах (рисунок 7)  .

Рисунок 7. ЛАЧХ и ЛФЧХ системы

          Как видно из рисунка 7, система обеспечивает запас по амплитуде 6 дБ и запас по фазе 19 градусов, что не соответствует требованиям, указанным в задании. Время переходного процесса с удовлетворяет требованию задания. Для того чтобы обеспечить выполнение всех условий задания, необходимо включить в схему управления дополнительное, управляющее корректирующее устройство.

6.  Синтез управляющего устройства.

Воспользуемся наиболее простым и наглядным методом логарифмических частотных характеристик. Суть метода заключается в следующем. Исходная ЛАЧХ системы не удовлетворяет всем заданным требованиям (рисунок 7). Строится желаемая ЛАЧХ системы, удовлетворяющая всем требованиям технического задания. Затем из ординат желаемой ЛАЧХ вычитаются ординаты исходной  располагаемой  ЛАЧХ  при  одинаковых  частотах.  В  результате  получаем ЛАЧХ  управляющего  устройства,  получаем  передаточную  функцию  и  принципиальную схему устройства.

Перенесём ЛАЧХ  L_ис(ω) исходной системы с рисунка 7 на рисунок 8. На рисунке 8 построим желаемую ЛАЧХ  L_ж(ω). При выборе желаемой ЛАЧХ необходимо, чтобы она удовлетворяла заданным требованиям и на каждом из частотных участков возможно меньше отличалась от исходной. Это позволяет получить более простые управляющие устройства.

Определим  вид  желаемой  ЛАЧХ  L_ж(ω)  в  области  средних  частот.  Частота среза определяется по формуле 

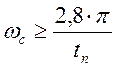                                            (39)

          Пусть t_n=3,5c, тогда 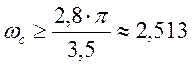. Проведём через точку ω_c прямую с наклоном  -20 дб/дек (рисунок 8). Из точки L = 20lgK  по оси ординат проводив линию с наклоном -40дб/дек. Точка пересечения этой линии и линии, проведённой через ω_c, даст частоту сопряжения ω₁ = 1/T₁. Таким образом, вид желаемой ЛАЧХ для частот ω < ω_c найден.

В  высокочастотной  области  желательно,  чтобы  желаемая  ЛАЧХ  возможно

меньше отличалась от исходной. Из точки ω = 1/T  опускаем перпендикуляр до пересечения с прямой, проходящей через ω_c . Из точки пересечения проводим прямую с наклоном  -60 дб/дек.

Рисунок 8. Исходные и желаемые логарифмические характеристики

По  виду  желаемой  ЛАЧХ  L_ж определяем  желаемую  функцию системы.

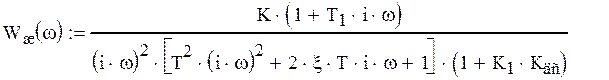                        (40)