Разработка системы автоматического управления промышленным оборудованием, страница 2

Раскроем типовую структуру САУ (рисунок 1) до функциональной схемы

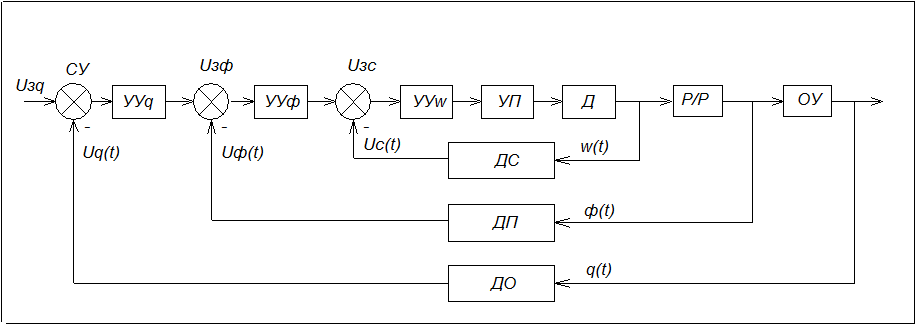
    Рисунок 2. Функциональная схема типовой САУ.

На рисунке 2 обозначено: ОУ - объект управления; СУ_q, СУ_φ, СУ_w -  сравнивающие  устройства (измерители  рассогласования)  координат q(t) объекта  управления,  угла  поворота  φ(t)  электродвигателя w(t)  соответственно; УУ_q, УУ_φ, УУ_w – управляющие устройства по  соответствующим  координатам;  УП –  усилитель-преобразователь; Д, 1/Р – электродвигатель постоянного тока; Р – редуктор; ДС, ДП, ДО – датчики скорости, положения (угла поворота) вала электродвигателя, координаты объекта.

Система (рисунок 2) состоит из трёх контуров. Первые два внутренних контура составляют САУ  электропривода. Внешний контур – контур непосредственного управления производственным процессом.

Принцип  работы  системы  следующий. Датчик  объекта  измеряет  координату U_q(t), которая сравнивается в СУ_q  с  заданным  значением U_зq(t). На основании этого вырабатывается  рассогласование (ошибка) e_q(t).  По  величине  ошибки e_q(t)  управ ляющее устройство УУ_q вырабатывает управляющее воздействие U_зφ(t) – требуемое значение угла поворота электродвигателя φ(t),  которое  сведёт ошибку  e_q(t) к нулю. Оно  сравнивается  с  текущим  значением  угла U_φ(t),  которое измеряется датчиком угла. В результате сравнения вырабатывается ошибка  e_φ(t) в управляющем устройстве угла УУ_φ  вырабатывается управляющее воздействие U_зc(t) – требуемое значение скорости поворота вала электродвигателя, которое сведёт ошибку e_φ(t) к нулю. Требуемое  значение U_зс(t) обрабатывается в первом внутреннем контуре – контуре регулирования скорости электродвигателя. Оно сравнивается с текущим значением скорости U_w(t), которое измеряет датчик скорости (ДС). В результате сравнения вырабатывается ошибка e_w(t) в управляющем устройстве скорости УУ_w вырабатывается управляющее воздействие U_y(t). В зависимости от Uy(t) усилитель - преобразователь вырабатывает  такое напряжение в цепи якоря  электродвигателя U_я(t), которое сводит ошибку по скорости e_w(t) к нулю.

Подавляющее  большинство  САУ  являются  сложными,  многоструктурными, многосвязными системами. Расчёт и проектирование таких систем представляет собой  сложную  трудоёмкую  задачу и начинается  с получения математических моделей звеньев и системы.

2.  Получение математических моделей САУ.

Динамика  большинства  производственных  механизмов  может  быть  описана дифференциальным уравнением второго порядка.

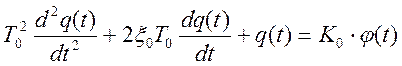                         (1)

где q(t) – управляемая переменная, φ(t) –  угол поворота вала электродвигателя (рад), Т₀ – постоянная времени объекта управления (с), ξ₀ – дискремент затухания, К₀ – коэффициент передачи объекта управления.

Применив  преобразование Лапласа  к  уравнению (1)  при  нулевых начальных условиях, получим

           (2)

Из уравнения (2) получим передаточную функцию объекта

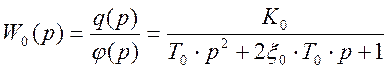                                   (3)

В  ряде  случаев  коэффициент  Т₀² на  порядок,  два  порядка  меньше  коэффициента  2ξ₀Т₀, поэтому первым членом уравнения (1) пренебрегают. Кроме этого динамика большинства  производственных  процессов  может  быть  описана  апериодическим звеном

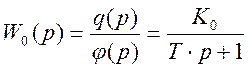                                              (4)

Электродвигатель постоянного тока описывается системой уравнений

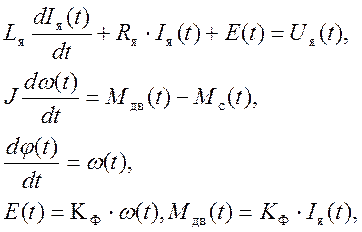                   (5)

где L_я – индуктивность цепи якоря (Гн);  I_я(t) – ток в цепи якоря (А);  R_я - сопротивление цепи якоря (Ом);  E(t) – ЭДС вращения (В);  U_я(t) – напряжение цепи якоря (В);  J – приведённый момент инерции (кг·м2);  w(t) – угловая скорость вращения вала двигателя (рад/с);  Мgв(t) – движущий момент на валу двигателя (Н·м);  φ(t) – угол поворота (рад);  К_Ф – коэффициент ЭДС (В·с).

Применив преобразование Лапласа для уравнений (5) при нулевых начальных

условиях и выполнив несложные преобразования, получим

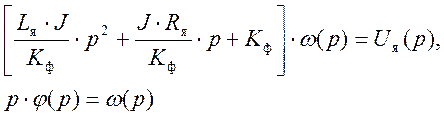                            (6)

Разделим  левую  и  правую  части  первого  уравнения  на  К_Ф,  умножим  и  разделим первый коэффициент первого уравнения на R_я

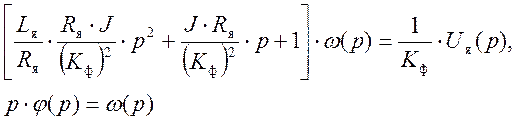                    (7)

Введём  обозначения L_я/R_я  =  Т_э –  электромагнитная  постоянная  времени  двигателя (с); J·R_я/(К_Ф)² = Т_м  –   электромеханическая   постоянная   времени   двигателя  (с); 1/К_Ф = К_ДВ – коэффициент передачи двигателя (рад/с).

Коэффициент ЭДС двигателя

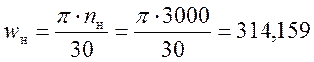рад/с

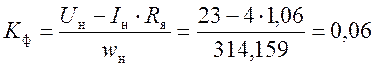
где U_н ,I_н ,w_н , n_н – номинальные значения параметров двигателя.

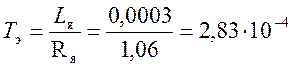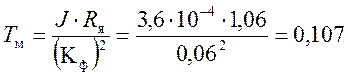с;

с;

.

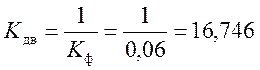Из выражения (7) получаем передаточные функции двигателя.

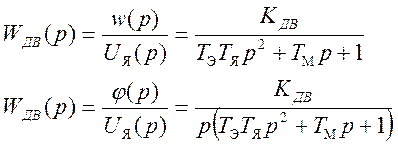                        (8)

Передаточные функции (8) допускают упрощения. При Т_м>Т_э передаточные функции (8) представляют в следующем виде

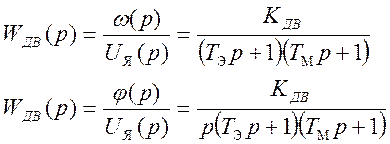                         (9)

Для многих двигателей Т_э·Т_м<< Т_м и  передаточные функции упрощаются до звеньев

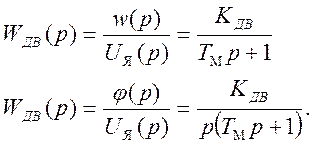                          (10)

Так как , передаточные функции двигателя принимают вид

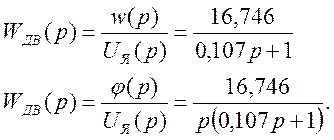                       (11)

Линеаризованные уравнения усилителей – преобразователей имеют вид

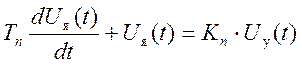                            (12)

где U_я(t) –  напряжение  якорной  цепи  электродвигателя (В). U_у(t) –  напряжение управления на входе усилителя – преобразователя (В). Т_n – постоянная времени (с). К_n – коэффициент передачи.

Применим преобразование Лапласа к уравнению (12), получим передаточную функцию усилителя – преобразователя

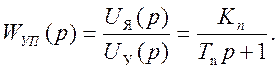                                                                                 (13)

Подставив численные значения, получим

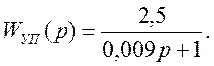                              (14)

Датчики считают безынерционными и описывают передаточными функциями

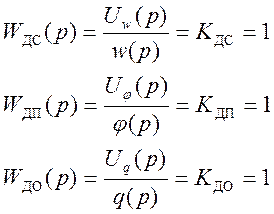                                (15)

Сравнивающие устройства описывают операторными уравнениями вида

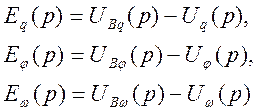                                  (16)

Математические модели управляющих устройств неизвестны. Их необходимо получить  такими,  чтобы  они  обеспечивали  устойчивость  и  заданное  качество  управления.