Предмет, цели и задачи моделирования. Классификация и свойства моделей. Этапы моделирования. Система и внешнее окружение. Методы создания моделей. Регрессионный анализ и модели на основе регрессий

1.Предмет, цели и задачи моделирования. Классификация и свойства моделей.

 

Эксперимент («натурный»):  var (x_i)ày_i

={x₁,x₂,…,x_n}

Недостатки:

1.  Необходимость воздействия на объект

2.  Не обладает повторяемостью

3.  Высокая стоимость ($↑)

4.  Продолжительные (∆ τ ↑)

Недостатки натурного эксперимента убрали и получили «вычислительный эксперимент», но не все.

Для вычислительного эксперимента необходимо наличие модели – это заменитель объекта для проведения с ним эксперимента.

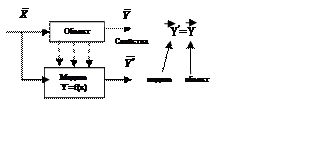Моделирование  - это исследование свойств объекта при помощи эксперимента на модели.

Система – целостное подмножество элементов и связей между ними.

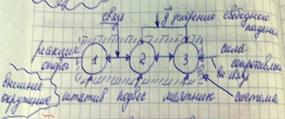
Топологией называется совокупность связей передающее взаимодействие между элементами системы.

Эмерджентность – это свойство системы отсутствующее у отдельных элементов.

Модели:

1. Натурная (реальная) – это замена одного

объекта другим

2. Знаковые  - некоторое описание объекта

Вербальные (описательные) Пример: уголовный кодекс

3. Формализованные (Примеры: ноты)

аналитическая (получение конечной формулы)

-алгоритмическая

-(программная) – реализация алгоритмической на ЯП

-имитационная

Задачами моделирования являются:

1. Разделение системы и внешнего окружения

2. Формализация системы (ведет к построению аналитической модели)

- алгебраическая y=f(x)

- обыкновенные дифференциальные  уравнения

-  дифференциальные  уравнения частных производных

-  Интегральные дифференциальные уравнения

3. Принятие допущений, которые упрощают модель.

4. Оснащение модели – постановка уравнения состояния, const, свойств объекта

5. Задания граничных (дифференциальные  уравнения частных производных) и начальных (дифференциальные уравнения) условий.

6. Метод решения

7. Переход к алгоритмической модели

8. Программная модель

9. Расчет по модели (получить y^’)

10.  Проверка адекватности (погрешности) – проводиться на основании тестового примера, который имеет легко получаемое аналитическое решение.

Если модель не адекватна, то происходит возврат 1-9.

Классификация моделей

1. Статической (независим от времени y=f(x)) и динамической (зависит от времени y=f(x,τ))

2. Непрерывные ({y,x}принадлежит R)и дискретные (каждая величина это набор каких-то возможных значений y=<y₁,y₂,..,y_n> n не стремится к∞)

3. Детерминированные (y=(M[y],D[y]) при x₁=3+/-1) и стохастические

4. Точечные (сосредоточенные y=f(τ) y:x принадлежит X) и распределенные (параметрическими y=f(x₁,x₂,τ)  (x₁,x₂ принадлежит X))

5. Линейные ( ), нелинейные (y=exp(a*x))

 Линеаризация модели

2.Этапы моделирования. Система и внешнее окружение. Методы создания моделей.

Методы создания моделей

1. Функциональный метод – сводиться к решению обратной задачи моделирования

                                          y=f(x)

             «прямая»                          «обратная»

                             «идентификации»

 

                                                                                          

 

<x_i,y_i>, i=1,N

xc{x₁,x₂,…,x_n}    регрессияà

yc{y₁,y₂,…,y_n} f(x):/y(x_i)-y_i/àmin

2. Структурный метод – построение иерархических моделей.

Принципы:

1) По уровню абстрагирования (параметры и характеристики важные  на нижнем уровне перестают быть важными на верхнем).

2) Уровень сложности принимаемых решений

3) Уровень организационной структуры

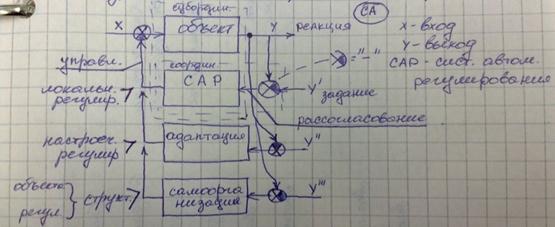
Построение структурных моделей производятся методом системного анализа, который позволяет свести сложную задачу к последовательности решения простых задач.

3.Основные понятия системного анализа. Типы систем управления. Построение моделей систем управления СА.

Двухуровневый алгоритм системного анализа.

Декомпозиция – разделение системы на элементы и связи между ними.

Агрегация – обратный процесс объединения решений задач для отдельных элементов.

Алгоритм предусматривает разные подходы к системе в целом и ее элементам.

Система	Элементы
Определение цели	Описание условий работы
Описание условий работы системы (разделение на систему и внешнее окружение)	Определение условий задачи Выделение критерия качества
Определение топологии                 (выделяются элементы и связи)	Моделирование элемента
	Поиск управления Анализ реализуемости
Агрегирование решения Заключение о достижения цели	Реализация Анализ свойств решения Заключение о качестве решения

Анализ свойств решения включает оценку погрешности (точности), устойчивости, чувствительности, пределов допустимости решения.

После каждого этапа возможно уточнение модели.

Второй уровень элемента может иерархически повторятся до глубины дек

4.Модели на основе фундаментальных физических законов (на примере уравнения теплопроводности). Дискретизация и решение уравнений частных производных.

Физические законы:

1. Законы сохранения

2. Законы движения

3. Законы состояния

Уравнение состояния

   

Уравнение движения

 

Уравнение сохранения

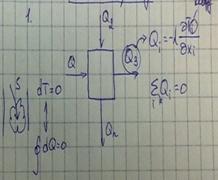
Предположим, что λ=const

   Фурье-Киргофа

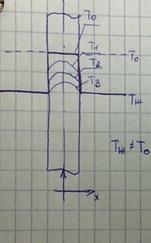
1)начальные условия T(x,0)=T₀x

2)граничные условия T(0,τ)=T(δ,τ)=T_ж(?)τ

Граничные условия 1: T (для простоты)

Граничные условия 2: q

Граничные условия 3: Q=α(T_нов-Т_ж)

 Теплоотдача

Методом решения дифференциальных уравнений является дискретизация

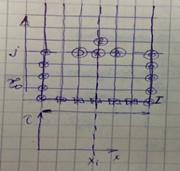
T(x), xRàT(x_i),x_i={x₁,x₂,…,x_n}

Н.у. T_i0=T₀, i=o,I

Граничные условия: T_0j=T_ж        j=0,1,2,…

                                           T_Ij=T_ж

Выделенный шаблон является иллюстрацией явного метода интегрирования диф. уравнений частных производных.

Алгоритм расчета:

1.  Задание начальных условий for i=0 to I do  T[i]:=T[o]

2.  Начало цикла (пока какое-то условие окончание не выполнено) условия окончания может быть: τ<τ_max, //T_ij+1-T_ij//<∆T_min, T_i0,j0>=T_{заданного}

2.1.  Граничные условия: T1[0]=T10;T1[i]:=T10(T_ж)

2.2.  Цикл i     T1[i]=T[i]+…(уравнение Ф-К)

2.3.  Цикл i     T[i]:=T1[i]

Если P=ρ(T)/λ=λ(T)/C=C(T)

2.1.а ρ_i=ρ(T_ij)->a_i

Модели на основе физических законов реально-применимы к простым заданиям.

5.Регрессионный анализ и модели на основе регрессий.

Регрессионный анализ.

 

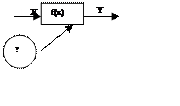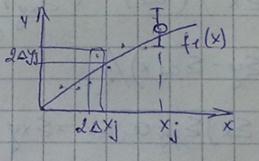
Наилучший <=>

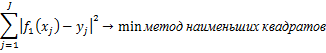
неизвестна

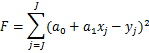
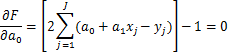
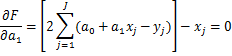
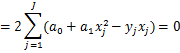
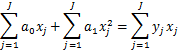
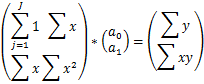
Аналогично записывается системы линейных алгебраических уравнений для полиномов высоких порядков

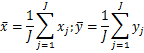
Многие функции можно привести к линейным преобразованиями

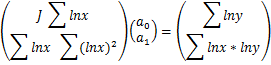
Существуют базисы неподдающиеся линеаризации

f₁(x)=a₀sin(a₁x)

Кроме того возможны функции от 2-х переменных

f₁(x₁, x₂)=a₀+a₁x₁+a₂x₂+a₁₁x₁²+a₂₂x₂²+a₁₂x₁x₂

Универсальным методом вычислений коэффициента является прямое решение задачи

На практике возникают проблемы:

I.  I. Проблема ошибок

1.{x,y}_j->{a_i}j

2. Ошибки:/ f₁(x_k)-y_k/≥ε(2…3δ)

Стьюдент

Лорд

…

3.k {x,y}_j->{a_i},j≠k

II. Проблема выбора функции

f₁(x)-?

Корреляция

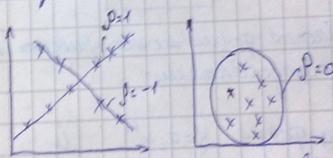
Коэффициент корреляции определяет возможность аппроксимации поведения объекта линейной функции

В любом случае погрешность определения коэффициентов снижается с увеличением количества экспериментов.