Предмет, цели и задачи моделирования. Классификация и свойства моделей. Этапы моделирования. Система и внешнее окружение. Методы создания моделей. Регрессионный анализ и модели на основе регрессий, страница 2

6.Основные понятия имитационного моделирования. Моделирование случайных чисел.

Аналитические методы -> подходят для простых систем и одиночных элементов

Имитационное моделирование  - это формальное описание логики функционирование системы и взаимодействие элементов, учитывающих наиболее существенные характеристики и связи для проведения статистических экспериментов.

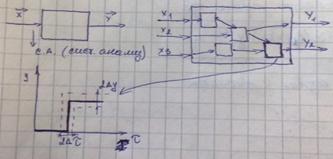
Статистический эксперимент – это поиск статистических характеристик систем проведением большого количества экспериментов.

Достоинства: метод позволяет исследовать без окончательной постановки задачи (точно не описан элемент); применим в сложных системах неописанных аналитически; позволяет выявлять новые эффекты в системе; хорошо подходит для тренажеров

Недостатки: требуется большое количество экспериментов для достижение объективности; результат носит частный характер (только в тех условиях, в которых он был получен); трудно искать ошибки.

Случайный процесс.

Рассмотри объект:

 

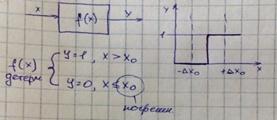
x₀: x₀±∆x₀

                f(x)= P(y=1/x≥x₀+∆x₀)=1

стохастическая  P(y=0/x≥x₀-∆x₀)=1

y(x] x₀-∆x₀+∆x₀[ )?

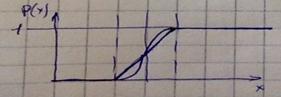
Вид распределения определяется природой объекта.

Случайный процесс называется марковским, если вероятность перехода в следующее состояние зависит только от состояния текущего момента, но не от истории объекта.

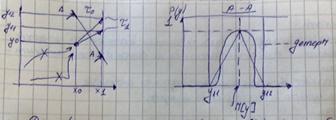
Для практического моделирования Марковских объектов требуется генерация случайных величин.

Моделирование случайных чисел

Random() – ?

Марковский генератор случайных чисел позволяет запрограммировать выбор следующего состояния марковского объекта.

Алгоритмы:

1.  t_i=0.0040353607;

t_i+1=(40353607*t_i)%1

t_i+1=(a+t_i)%1, a>>0, t_i<<1

для шифрования не пригоден, т.к. нужно взломать первое число и настроечный параметр.

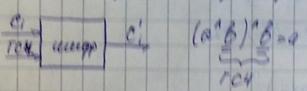
2.  t_i,ti₊₁ =(A+t_i+B)%C, C=2^M, M>1, B%2=1, A%4=1

Если M=8 то  t_i – байт

7.Дискретно-детерминированные и дискретно-стохастические модели. Способы записи функций переходов и выходов.

x{x₁,x₂,…,x_n}

Автомат консиный <=> количество значений на входе и выходе ограниченно.

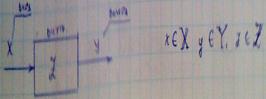
Z=Y(z,x) – функция переходов

Y=Ψ(z,x) – функция выходов

Автомат <x,z,y, y ,Ψ, z₀>

Автомат абстрактный – содержит 1 скалярный вход и 1 скалярный выход

Дискретность автомата – это его способность изменять состояние только в заданный момент времени.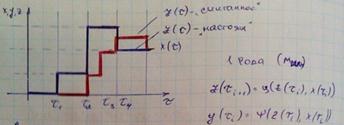

2 ряда z (τ_i+1)=φ(z(τ_i),x(τ_i))

y=(τ_i+1)=Ψ(z(τ_i+1),x(τ_i))              мур. y(τ_i+1)= Ψ(z(τ_i+1))

Без памяти

zø

y(τ_i+1)= Ψ(x(τ_i) – меняется выходной сигнал

Способы записей функций переходов и выходов

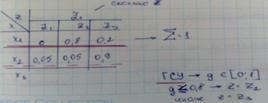
1. Табличный способ

№1

x    z	Z1	Z2	Z3	…
X1	Z2	Z2	Z1
X2	Z3	…	…
X3	…	…	…
…

x{0;1} выкл; вкл      z{0;1}   y=z

№2

x  y	0	1
0	0	0
1	1	1

	1	2	3	4	5	…
1	а	б	в	г	д
2	е	ж	…	…	…	…
…

Удобнее для алгоритмизации

2. 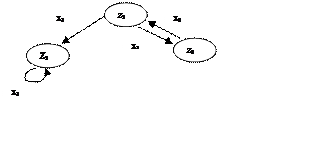Направленный граф

№1                                                                      

 

№2

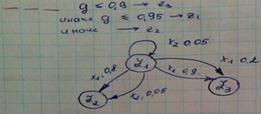
Запись в формате графа удобнее для аналитических исследований.

Дискретно-стахостические системы.

<x,y,z,φ,Ψ,z₀>  P-вероятность

<z₀,x₁>à(P)<z₁,y₁>

0≤P≤1

8.Системы массового обслуживания. Цели, задачи и определение путем имитационного моделирования характеристик систем. Средства моделирования.

- обслуживают покои заявок в каналах и очередях.

   

      X – интенсивность C^-1

      τ  - обслуживание время

      y – интенсивность потока обслуживания
    P(x,τ≥τ₀)

    P(y,τ≥τ₁)

Все величины заданы вероятностными распределениями

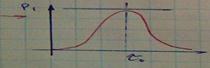
Поток заявок однородный, если все заявки одинаковы, в смысле их обслуживания (газовая заправка)

Поток ординарный, где все заявки не могут поступить сходу.

Обслуживание заявок = ожидание (очередь) +обслуживание (канал)

Приоритет заявки – определяет порядок сортировки при ожидании

 - не вытесняющий

- вытесняющий – если приоритетная заявка прерывает выполнение предыдущей.

Прерывание заявки может восстанавливаться или нет.

Поток равномерный, если интенсивность не меняется со временем.

Каналы характеризуются:

1. Временем обслуживания или его распределения

Канал специализированный, если может обслужить только часть заявок неоднородного потока.

Канал характеризуется в состоянии доступности, если он способен обслуживать заявки. Если канал неспециализированный, то он универсальный

Доступность

Восстановление       Прерывания

Прзх

Канал может быть занят или свободен

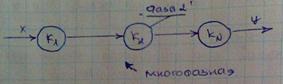
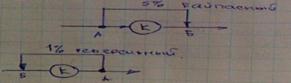
                         Источник (вводит заявку)

 

                     Терминатор (прекращает заявку)

Исследования СМО:

1. Аналитическая            на СОМУ (надежные автоматизированные системы обработки массового управления) 2.Имитационные

Имитационное моделирование.

Цель (СМО)– исследование статистических распределений характеристик СМО.

Характеристики:

1. Загрузка канала                                        нулевые

2. Длина очереди                                           min

3. Количество отказов в обслуживании      средние

4. …                                                               max

Задачи:

1. Построение СМО

2. Планирование эксперимента (сколько экспериментов?)

                    к.р.                10 экспериментов    

3. Условия (начальные, окончания и д.р.)

4. Проведения эксперимента

5. Вычисление характеристик

Свойства моделирования СМО:

1. Язык программирования высоких уровней

2. Языки имитационного моделирования (GPSS)

3. Системы имитационного моделирования (MatLab+Stateflow, Stratum)

GPSS: + специализированный, гибкий

            - много версий (Dos,W95,sdutent), отладка, медленный, т.к. интерпретатор.

9.Организация модельного времени. Принцип обратного отчета.

                          время моделей

Модель             время заявки            условные (маштаб)

                          время расчета, сек

Масштаб обеспечивает переход от времени модели к времени объекта. Любое время можно определить окончания моделирования.

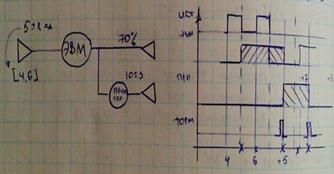
Возможны два варианта организации модельного времени:

1. Метод особых состояний – вычисляет момент особого следующего состояния:

а) Вход заявки системы

б) Вход в устройство

в) Изменение устройства

г) Выход из устройства

д) Выход из системы

е) Окончания моделирования

2. ∆t – весь интервал моделирования делиться на отрезки

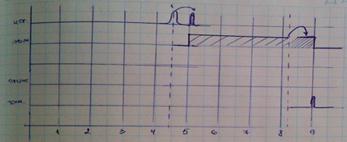
∆t   + проще  

       - обладает неустранимой погрешностью

Метод обратного отчета заключается в переборе устройств от терминаторов к источникам (особенно важно и в методе ∆t).

10.Планирование эксперимента. Полнофактроный и дробнофакторный эксперимент.

Моделирование

Исследов                                             получение экстр хар-к

                             Эффективн.

При проведении моделирования необходимо обеспечить эффективность моделей и плана проведения эксперимента. Эффект модели - адекватность, точность, производит и т.д. План определяет объём и порядок проведения экспериментов, т.е. процесс использования моделей.