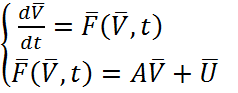Другие предметы \ Моделирование систем управления

Построение математической модели изгиба прямоугольной мембраны на основе теории распределенных сигналов, страница 5

                                                                                                 (2.24)

где      А – матрица Якоби динамической системы,

 вектор фазовых координат,

 вектор невязок,

 вектор функции внешних воздействий.

С учетом произведенных ранее расчетов запишем систему дифференциальных уравнений, составляющую динамическую гидросистему:

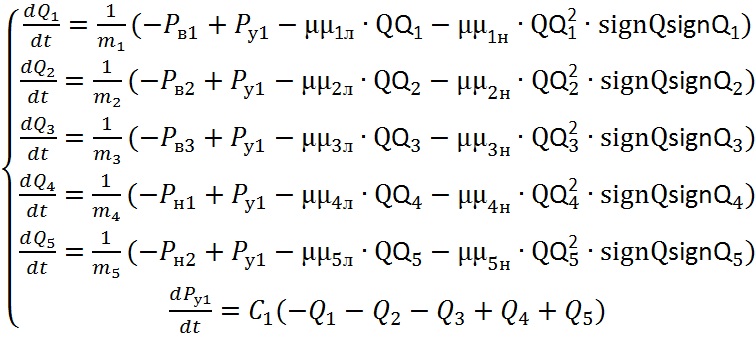                            (2.25)

Так как система дифференциальных уравнений нелинейная, то элементами матрицы Якоби являются частные производные по фазовым координатам:

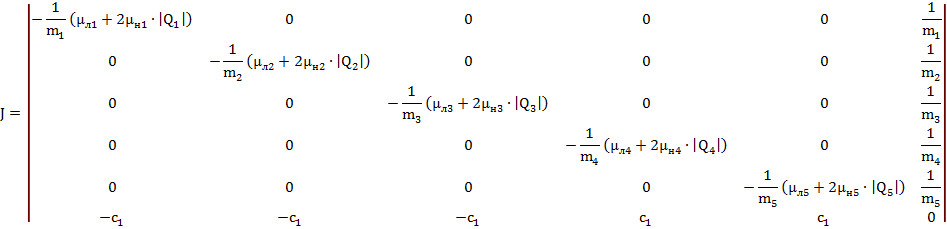
Переходную характеристику определяют в результате численного интегрирования системы дифференциальных уравнений, для чего необходимо провести выбор ряда параметров.

Пусть переходный процесс оценивается как реакция системы, находящейся в состоянии покоя на ступенчатое воздействие вида:

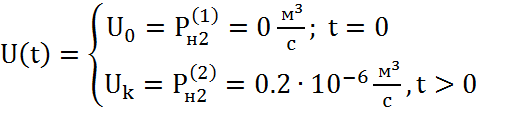                                                                                                 (2.26)

где  и  – начальные и конечные значения функции воздействия u(t), причем  и  – const .

Начальные и конечные значения всех фазовых координат определены при анализе статического состояния (таблица 2.5)

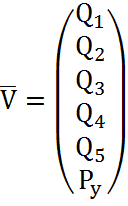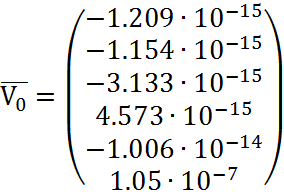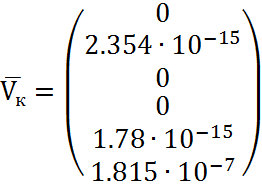,   ,              (2.27)

Если система устойчивая, то через некоторый промежуток времени система придет из состояния V0 в состояние Vk. Для численного интегрирования будем использовать неявный метод Эйлера. Вектор входных воздействий при t≥0 имеет вид:

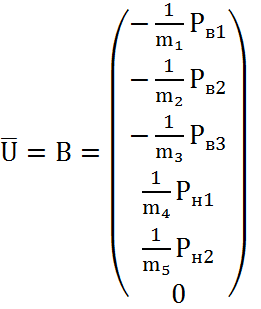                                                                                                 (2.28)

Формула численного интегрирования метода Эйлера имеет вид:

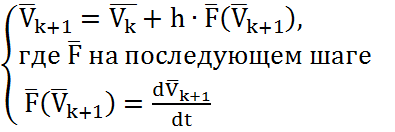                                                            (2.29)

Совместное преобразование двух последних выражений приводят к записи:

                                                                                             (2.30)

где        – модифицированная матрица Якоби на (к+1) шаге, которая формируется по следующим правилам:

Диагональные элементы матрицы Якоби на k-ом шаге пересчитываются по формуле:

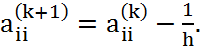                                                                                      (2.31)

Остальные элементы не изменяются:

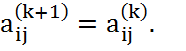                                                                                           (2.32)

 – модифицированный вектор входных воздействий на k+1 шаге.

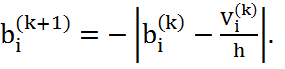                                                                                                                  (2.33)

Решение системы уравнений дает значение фазовых координат на к+1 шаге, т. е. в момент времени .

Алгоритм неявного метода Эйлера с постоянным шагом интегрирования h:

1) задание шага интегрирования h

2) задание начальных значений переменных при t0=0;

3) вычисление времени tk+1=tk+h, где k=0,1,2… ;

4) вычисление матриц  и  на к+1 шаге

5) Решение системы уравнений  с целью определения  в момент времени tk+1;

6) Переход к этапу 3 до тех пор, пока в случае устойчивой системы фазовые координаты не достигнут состояния конечного значения или не будут доказательства неустойчивой системы.

Начальные значения вектора  определяется на основании входных воздействий системы. В качестве начальных значений фазовых переменных берем вектор начальных значений .

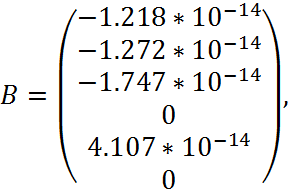
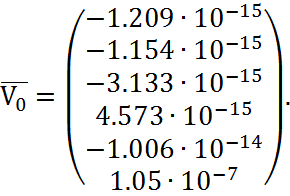
                                                                                                         (2.34)

Переходные процессы гидросистемы представлены на рисунке 2.4 и рисунке 2.5.

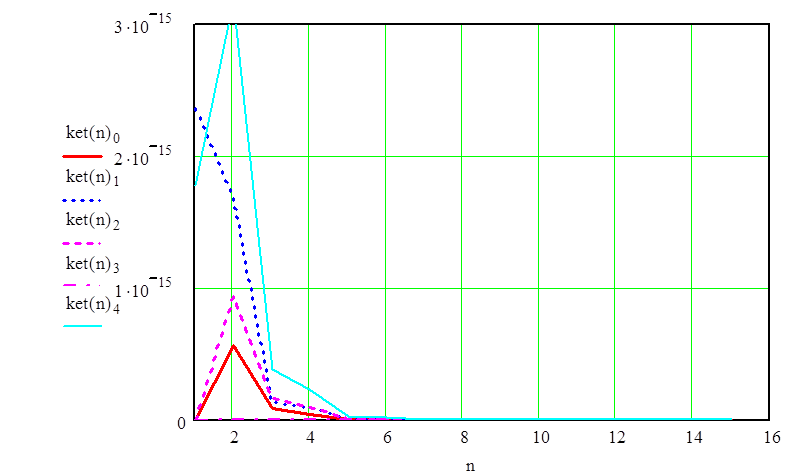
Рисунок 2.4 – Переходные процессы расходов Q1, Q2, Q3, Q4,Q5

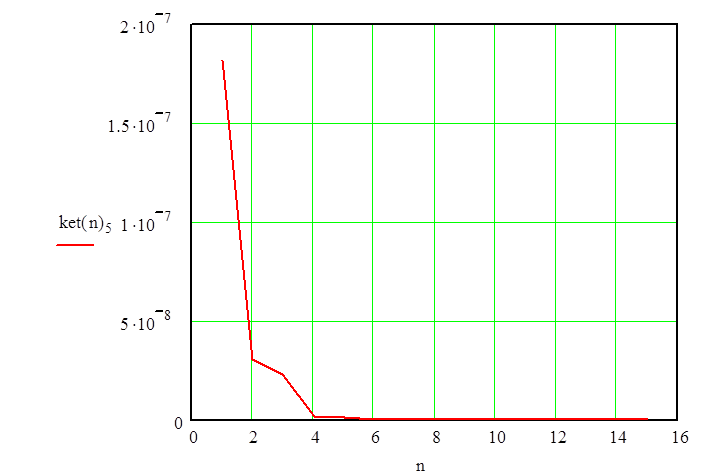
Рисунок 2.5 – Переходный процесс гидросистемы


ЗАКЛЮЧЕНИЕ

В ходе выполнения курсовой работы произведено моделирование на

микроуровне и макроуровне.

Изучена теория систем с распределенными параметрами применительно к конкретной выбранной задаче математической физики, произведен расчет выходной распределенной величины, интегральной передаточной функции, построены логарифмическая характеристика и ее аппроксимация стандартными типовыми наклонами.

На стадии моделировании на макроуровне исследовали статическую и динамическую модель гидросистемы. Решена система дифференциальных уравнений статической модели методом Ньютона, а динамическую модель рассчитали методом Эйлера. Построен переходной процесс системы.


СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1.     Бутковский А.Г., Характеристики систем с распределенными параметрами. Наука, 1979.-224с.

2.     Бессекерский В.А., Попов Н.П. Теория систем автоматического регулирования. М.; Наука 1966.-992с

3.     Власов В.В. Синтез интегральной передаточной функции для объектов управления с распределенными параметрами. //Школа академика Власова: Сб. метод, тр-М.,Буркин, 1998.-128с.


ПРИЛОЖЕНИЕ А

(Обязательное)

Графическая часть.

1 Моделирование на микроуровне. Идентификация краевой задачи                                                                                                       31

2 Расчет выходной распределенной величины                                                                                                       32

3 Расчет динамической характеристики                                                                                                       33

4 Моделирование на макроуровне. Исходные данные                                                                                                       34

5 Графические формы математической модели гидравлической системы                                                                                                       35

6 Расчет статического режима работы гидросистемы                                                                                                       36

7 Расчет динамического режима работы гидросистемы                                                                                                       37

Скачать файл