Построение математической модели изгиба прямоугольной мембраны на основе теории распределенных сигналов, страница 2

Проследим за соблюдением размерности.

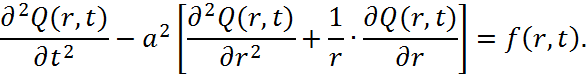
Проверим размерности величин:

Q(r,t)-деформация мембраны, м;

f(r,t)-входное воздействие на мембрану, м/с²;

а – волновая скорость мембраны, м/с.

Учитывая размерности всех коэффициентов и величин, входящих в данное уравнение, получим:

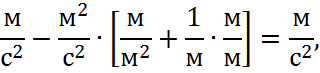
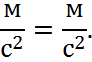
Размерность соблюдается, следовательно, все коэффициенты подобраны верно.

1.3 Расчет выходной распределенной величины

Зная стандартизирующую функцию и функцию Грина, можно найти выходную функцию, вычислением интеграла, представляющий собой основное отношение, связывающее выход объекта при заданном начальном состоянии с входными воздействиями:

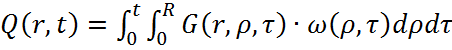                                                                                                                    (1.3)

В данном случае примем радиус мембраны и время соответственно R=2 м и t=1 c . Вычислим интеграл, связывающий выход объекта при заданном начальном состоянии с выходными воздействиями:

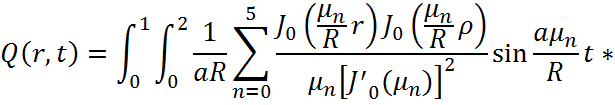
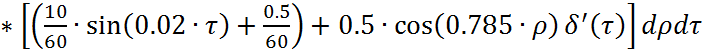                                                                                                                     (1.4)

Причем

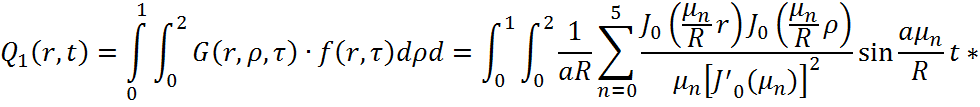
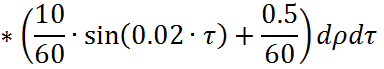
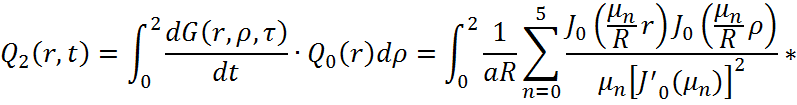
Определим значения  как корни уравнения:

Построим функцию Бесселя

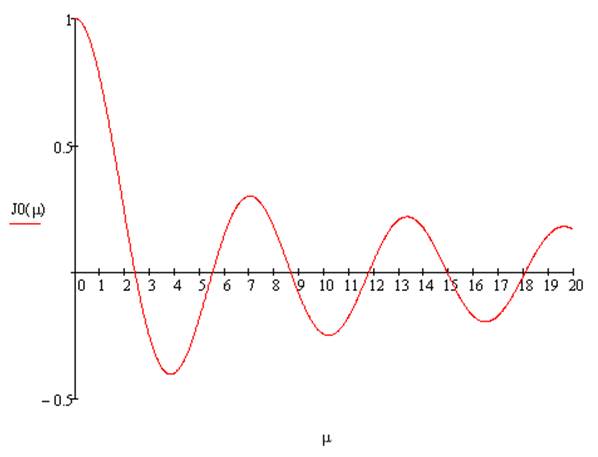
Рисунок 1.2- Функция Бесселя.

Представим функцию Грина в виде суммы слагаемых:

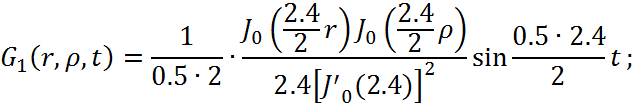
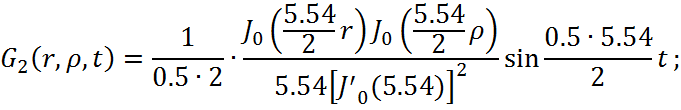
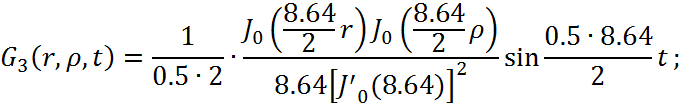
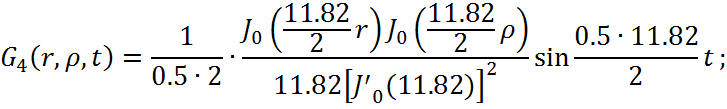
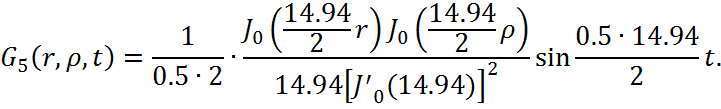
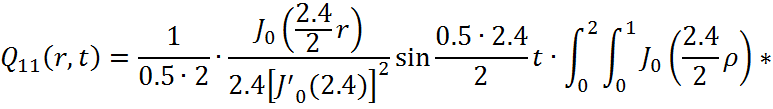
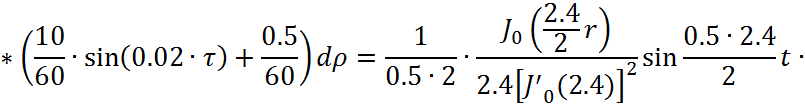
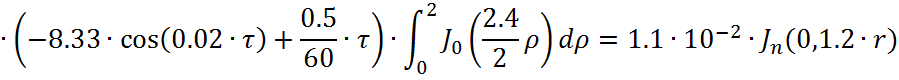
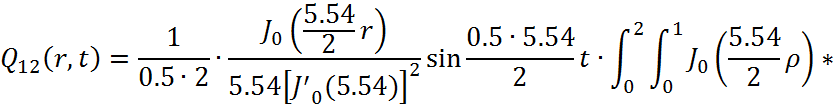
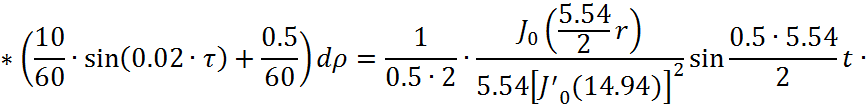
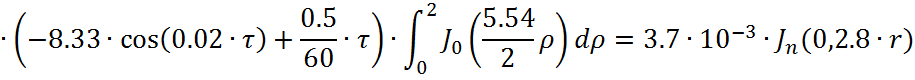
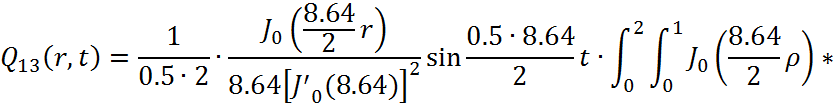
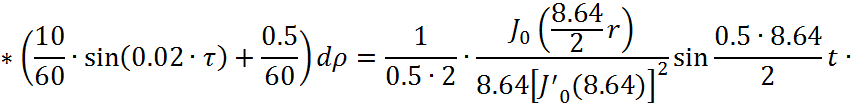
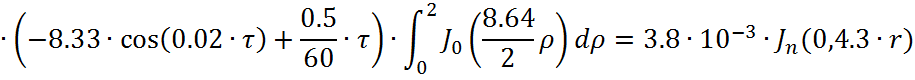
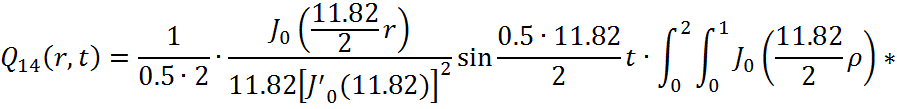
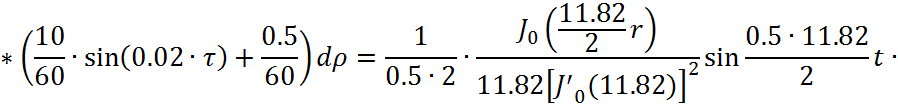
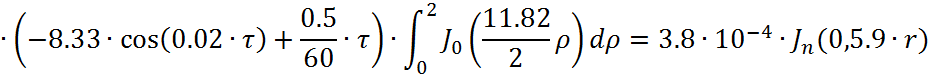
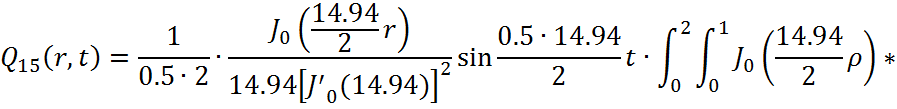
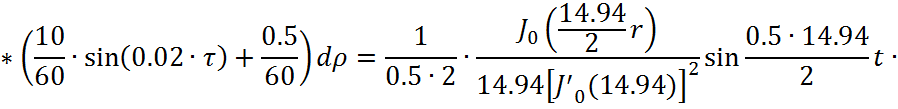
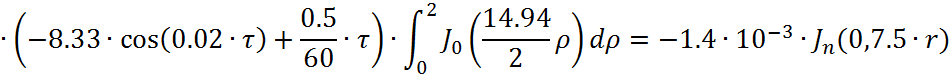
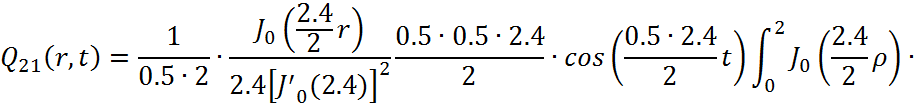
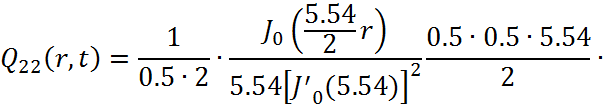
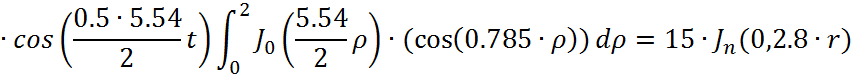
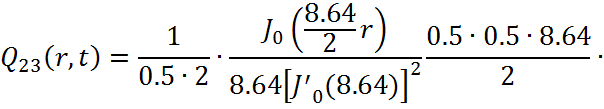
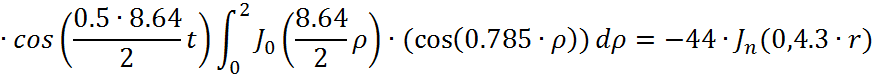
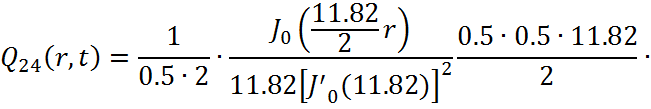
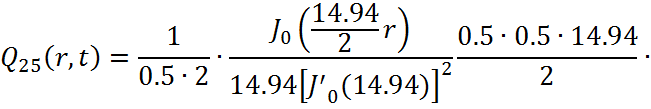
В результате получим уравнение выходной функции состояния объекта с распределенными параметрами:

                                                         (1.5)

Построим функцию колебания мембраны для t=1с и t=50с:

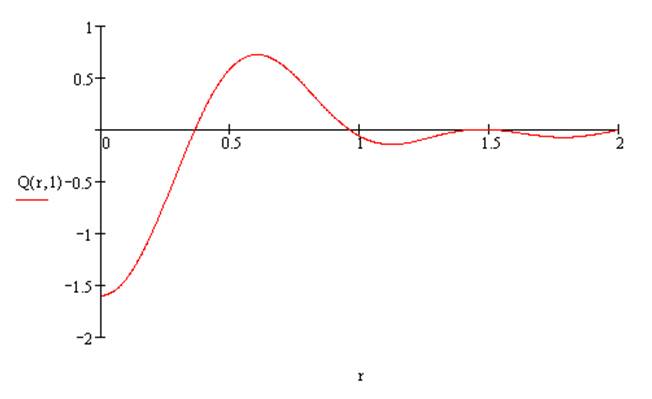
Рисунок 1.3 – График выходной величины Q(x,t) при t=1 c

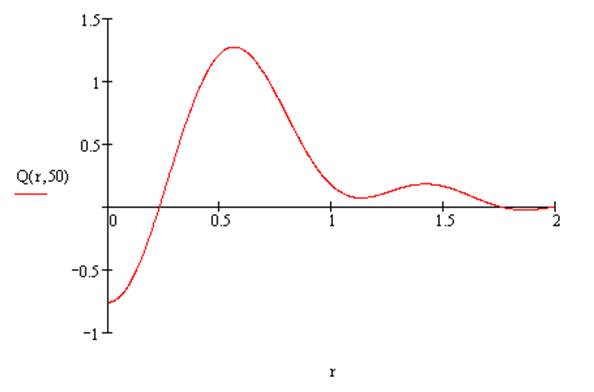
Рисунок 1.4 – График выходной величины Q(x,y,t) при t=50 c

1.4 Расчёт интегральной передаточной функции

По заданному дифференциальному уравнению объекта получим выражение для передаточной функции в распределённых параметрах.

Континуальная передаточная функция имеет вид:

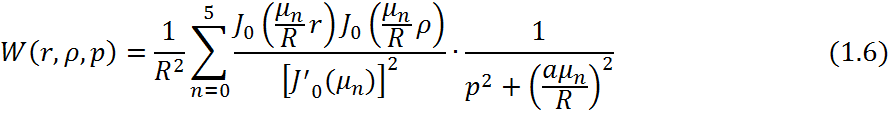
Стандартизирующая функция имеет вид:

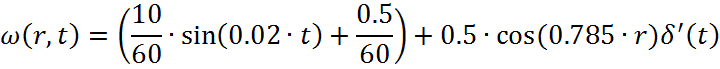
Преобразование по Лапласу стандартизирующей функции:

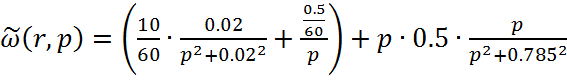                                         (1.7)

Вынесем за скобку входное воздействие, преобразованное по Лапласу:

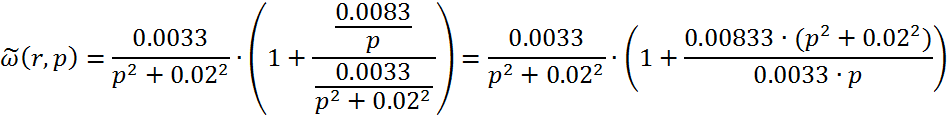
Рассчитаем интегральную передаточную функцию как пространственную композицию от произведения континуальной функции  

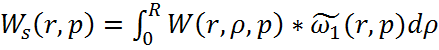                                                                                                                    (1.8)

Причем 

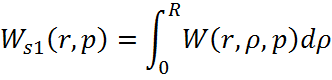
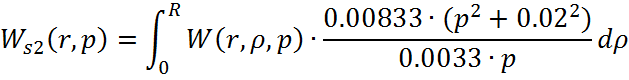
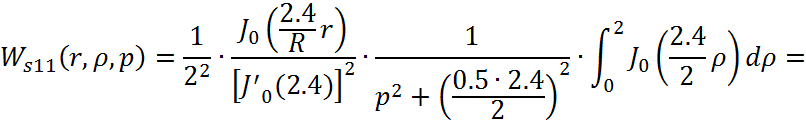
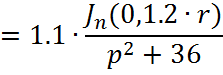
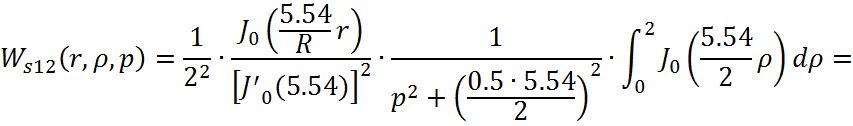
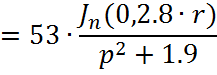
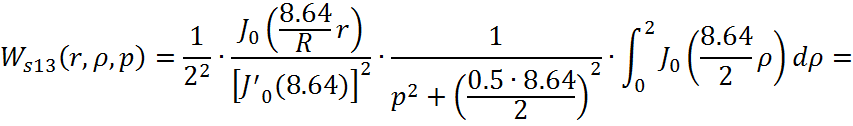
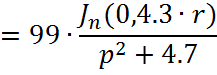
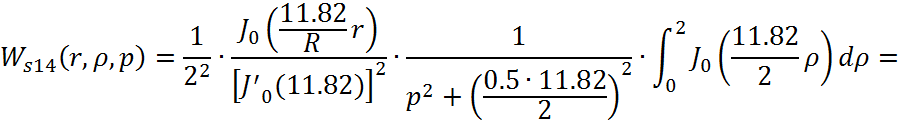
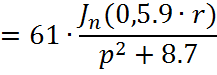
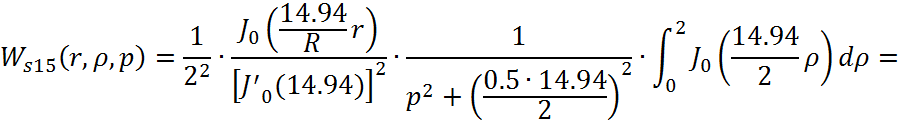
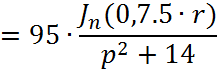
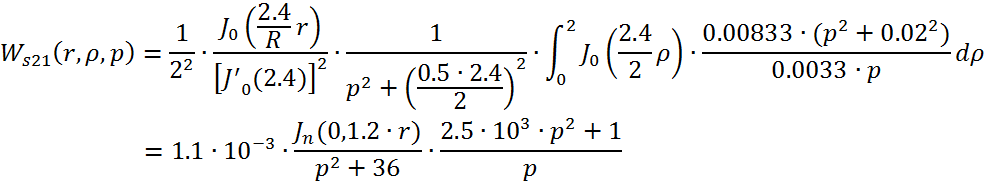
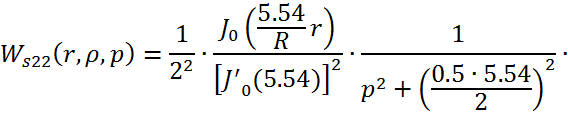
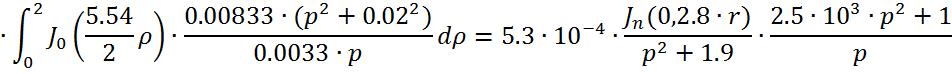
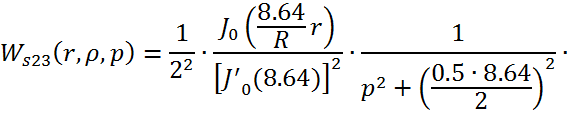
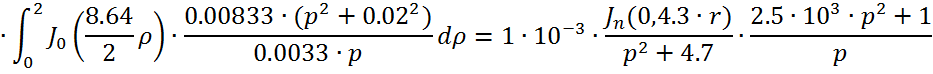
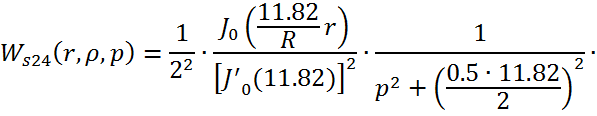
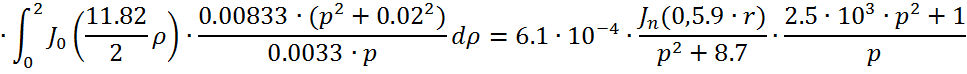
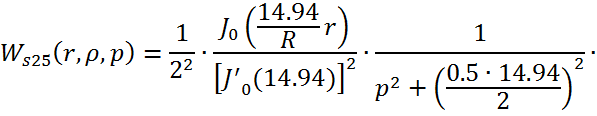
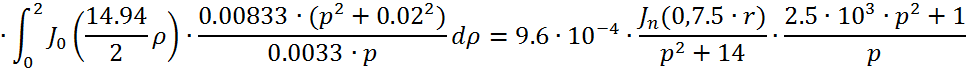
Следовательно получим:

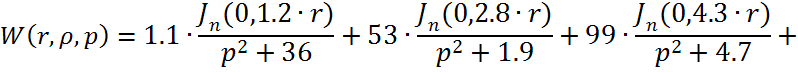
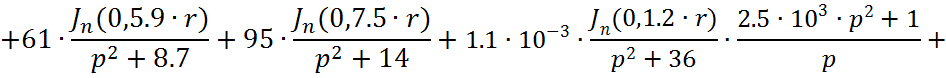
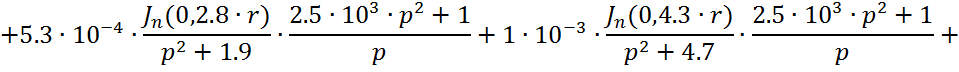
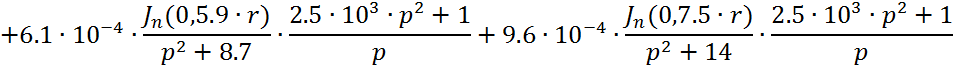
                                                                                                                                   (1.9)  

Примем 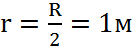 и , и получим выражение для частотной передаточной функции:

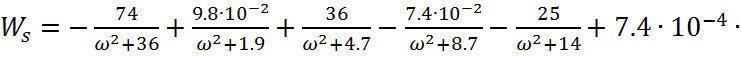
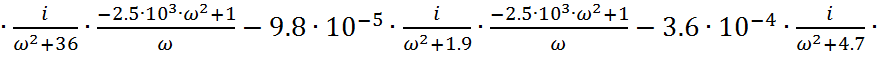
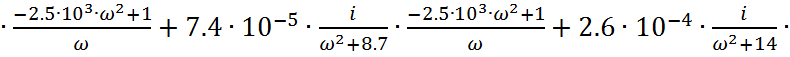
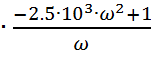(1.10)

1.5 Построение логарифмической амплитудно-частотной характеристики

Построим ЛАЧХ, аппроксимируем, и запишем выражение передаточной функции через типовые звенья.

Построим ЛАЧХ по выражению:

20log([W_s(ω)])

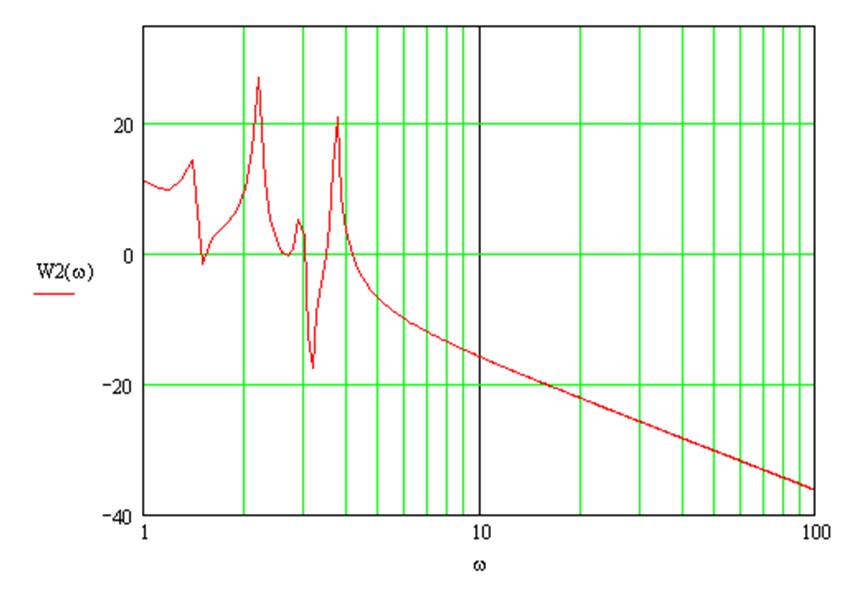
Рисунок 1.5 - График логарифмической амплитудно-частотной характеристики

Аппроксимируем полученную ЛАЧХ стандартными типовыми наклонами (+20дб/дек; -100 дб/дек; +80 дб/дек; -80 дб/дек; +80 дб/дек; -60 дб/дек; -40 дб/дек). Тогда передаточная функция будет иметь вид:

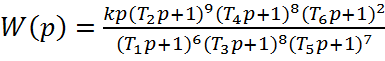                                                                                                  (1.11)

График ЛАЧХ пересекает ось y в точке -82.178, тогда коэффициент усиления равен:

20logk=11.097, следовательно k=3.588

Постоянные времени равны:

T₁=0.716; T₂=0.669; T₃=0,457; T₄=0,315; T₅=0,265; T₆=0,158

С помощью аппроксимации передаточная функция запишется в виде:

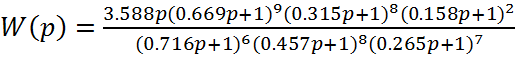                                                                                                 (1.12)

1.6 Моделирование круглой мембраны в среде Elcut          НЕ МОЁ!!!!!

Смоделируем колебание квадратной мембраны при нулевых начальных и граничных условиях, при входном воздействии . Построим двумерную модель в виде прямоугольника длиной 0.5 м, и высотой 1 м, зададим воздействия на ребрах модели и выберем свойства материала мембраны (сталь 20). Решение задачи получим виде цветовой схемы.

 

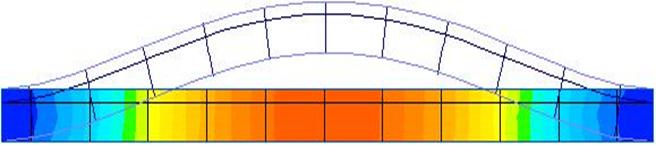
Рисунок 1.5 - Моделирование изгиба квадратной мембраны от начального положения

2. МОДЕЛИРОВАНИЕ НА МАКРОУРОВНЕ

2.1 Исходные данные

Дана схема гидравлической системы, представленная на рисунке 2.1. В системе используется в качестве рабочей жидкости веретенное масло АУ. Материал трубопровода – сталь. Основные параметры системы и жидкости приведены в таблице 2.1. Параметры трубопроводов приведены в таблице 2.2.

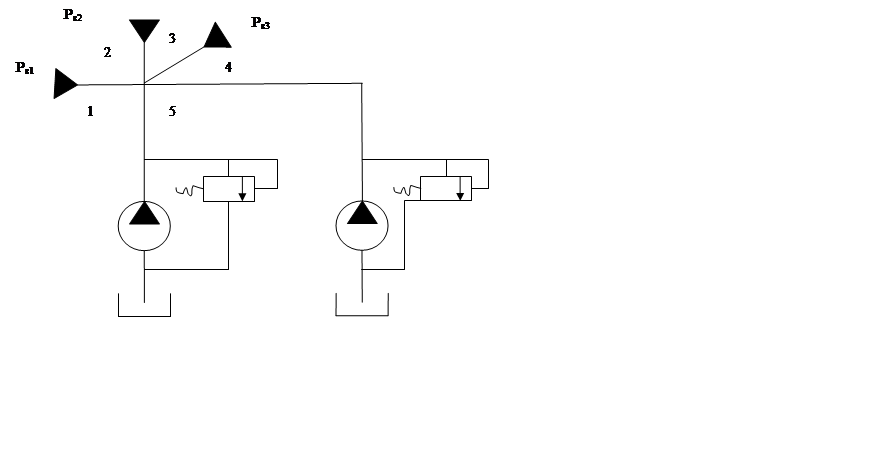
Рисунок 2.1 – Схема гидравлической системы: 1,2,3,4,5 – магистрали потребителей; Р_В1, Р_В2, Р_В3 – давление потребителей; P_H1, P_H2 – насосы.

Таблица 2.1 – Параметры системы и жидкости

Основные параметры	Обозначение	Значение
Плотность рабочей жидкости, кг/м3	ρ	860
Вязкость, м2/с	ν	0.15×10-4
Модуль упругости системы, Па	Eс	1.7×108
Модуль упругости трубопровода, Па	Eтр	2.1×1011
Коэффициент потерь на трение при турбулентном потоке	λт	0.03
Толщина стенки трубопровода, м	δтр	2.2×10-3

Таблица 2.2 – Параметры трубопроводов

Параметр	Обозначение	Номер трубопровода
		1	2	3	4	5
Диаметр трубопровода, м	dтр	0.010	0.015	0.015	0.015	0.015
Длина трубопровода, м	l	1.5	2.1	2	2	1
Коэффициент местных сопротивлений	ζ	4.5	6	5	5	3
Давление потребителей и насосов, МПа	p	0.2	0.13	0.17	0.2	0/0.2