2.2 Графические формы математической модели гидросистемы
На основании исходной принципиальной схемы гидравлической системы (рисунок 2.1) строится динамическая модель. Участки магистралей представляются как последовательное соединение инерционного и диссипативного элемента, причем для инерционного элемента указывается направление движения рабочей жидкости. В точки ветвления магистралей устанавливают упругие элементы, учитывающие сжимаемость жидкости и деформируемость стенок трубопровода. На рисунке 2.2 представлена полученная динамическая модель.
На основании динамической модели построен ориентированный граф, являющийся графической формой модели гидравлической системы. Узлы орграфа соответствуют сосредоточенным массам, а ветви - компонентам математической модели.
Базовый узел (с нулевым номером) отображает инерциальную систему отсчета фазовых координат типа потока. Источник обеспечивает возрастание потоковой переменной узла, поэтому сигналы направляют от базы к узлу. В магистралях потребителей – наоборот.

Рисунок 2.2 –Динамическая модель гидравлической системы
Во всех ветвях инерционных и диссепативных элементов направление сигналов от узла к базе. Такое направление характеризует затраты энергии источников на увеличение кинетической энергии и на трение. В ветвях упругих компонентов стрелки указывают направление передачи энергии от источников к потребителям. В ветвях всех элементов кроме направления записывается параметр каждого элемента. На рисунке 2.3 представлен полученный орграф.
2.3 Матричная форма математической модели
Для формирования полной математической модели на основе компонентных и топологических уравнений широкое применение получил узловой метод, для него необходимо сформировать матрицу инциденций, отражающую структуру связей всех элементов графа. Число строк матрицы соответствует числу узлов орграфа, число столбцов – числу ветвей. Отсутствие связи между узлом и ветвью обозначается «0», если ветвь входит в узел – «1», если выходит – «-1».

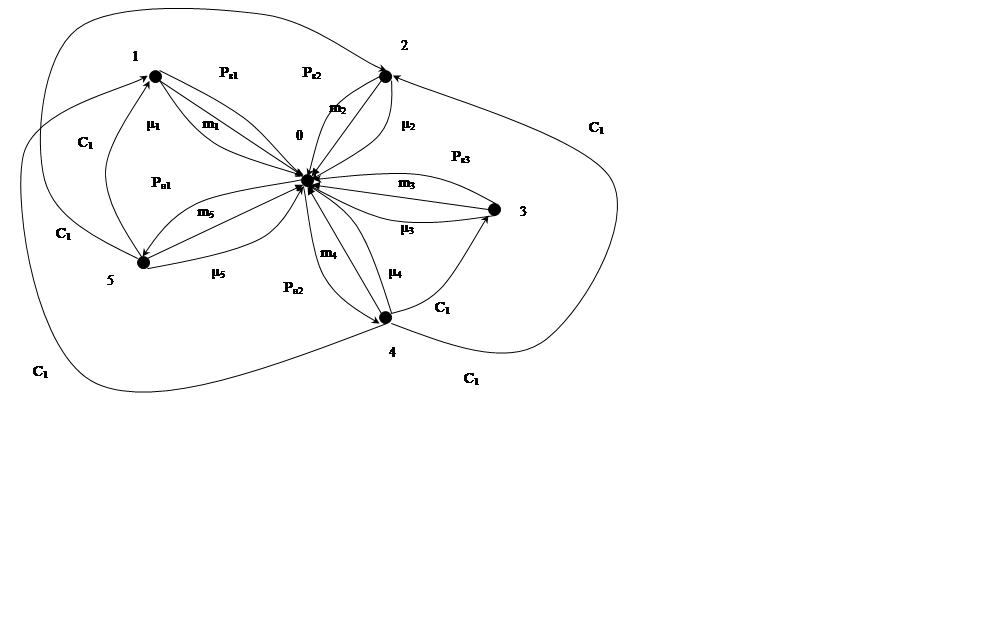
Рисунок 2.3 – Ориентированный граф гидравлической системы
Матрицу инциденций А можно представить состоящей из подматриц инерционных АИ, диссипативных АД, упругих АУ ветвей и подматрицы ветвей источников потенциалов АВ. Для исходной системы полечена матрица, представленная в таблице 2.3:
А=[ АИ, АД, АУ, АВ]
Таблица 2.3 – Матрица инциденций гидравлической системы
|
Узлы |
Ветви |
|||||||||||
|
Диссипативные узлы |
Упругие |
Внешнее воздествие |
||||||||||
|
μ1 |
μ2 |
μ3 |
μ4 |
μ5 |
С1 |
Pв1 |
Pв2 |
Pв3 |
Pн1 |
Pн2 |
||
|
1 |
-1 |
0 |
0 |
0 |
0 |
1 |
-1 |
0 |
0 |
0 |
0 |
0 |
|
2 |
0 |
-1 |
0 |
0 |
0 |
1 |
0 |
-1 |
0 |
0 |
0 |
0 |
|
3 |
0 |
0 |
-1 |
0 |
0 |
1 |
0 |
0 |
-1 |
0 |
0 |
0 |
|
4 |
0 |
0 |
0 |
-1 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
1 |
|
5 |
0 |
0 |
0 |
0 |
-1 |
-1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
Ав |
Ау |
Ад |
||||||||||
2.4 Узловой метод формирования математической модели
Из матрицы инциденций можно получить систему уравнений математически описывающие функционирование гидравлической системы:
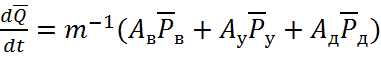 (2.1)
(2.1)
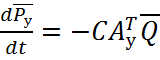 (2.2)
(2.2)
![]() (2.3)
(2.3)
где АД, АУ, АВ – подматрицы инциденций;
![]() – векторы давлений;
– векторы давлений;
![]() – векторы расходов;
– векторы расходов;
m, c,μ– диагональные матрицы параметров элементов гидравлической системы.
На основании матрицы инциденций запишем подматрицы упругих АУ, диссипативных АД элементов и подматрицу источников потенциалов АВ:
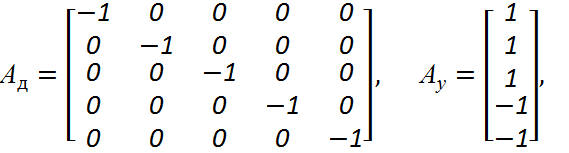
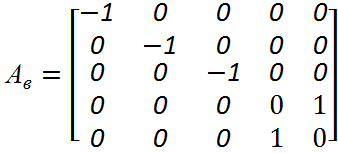
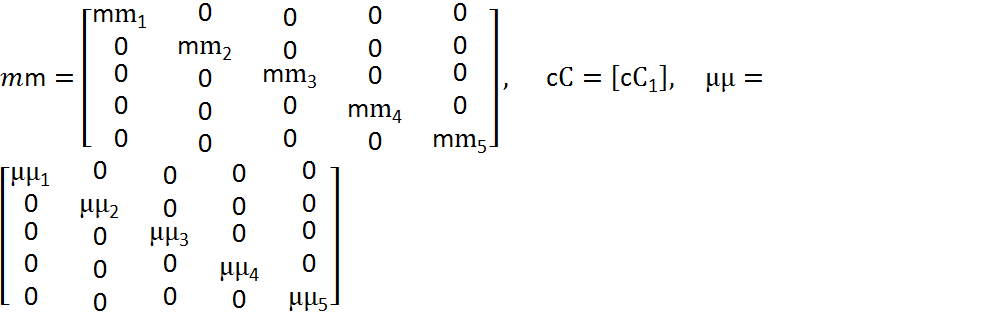 .
.
Рд, элементов и матрица фазовых переменных типа потока Q:
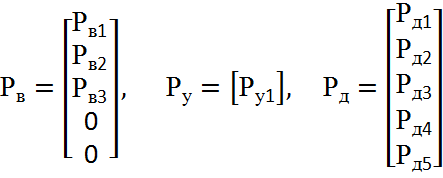 .
.
Для нашего случая система будет иметь вид:
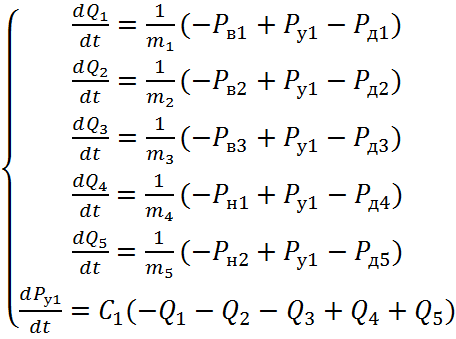 (2.4)
(2.4)
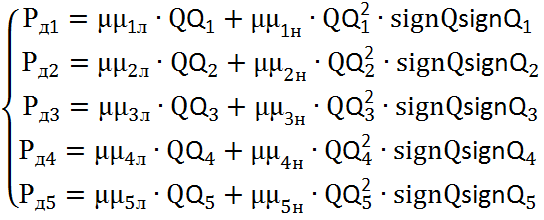 (2.5)
(2.5)
2.5 Расчет парметров трубопровода гидросистемы
Значения коэффициентов линейных и нелинейных потерь для конкретной магистрали находят по формулам:
- площадь сечения трубопровода, м2:
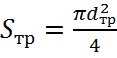 (2.6)
(2.6)
-объём трубопровода, м3:
![]() (2.7)
(2.7)
-доля объёма трубопровода
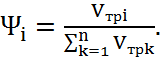 (2.8)
(2.8)
-коэффициент массы, кг/м4:
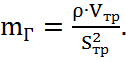 (2.9)
(2.9)
-коэффициент линейных потерь, Н·с/м5:
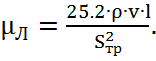 (2.10)
(2.10)
-коэффициент нелинейных потерь, Н·с/м5:
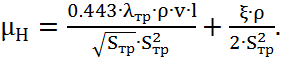 (2.11)
(2.11)
-коэффициент жёсткости участка, Н/м5:
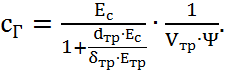 (2.12)
(2.12)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.