Построение математической модели изгиба прямоугольной мембраны на основе теории распределенных сигналов, страница 4

-коэффициент жёсткости элемента, Н/м⁵:

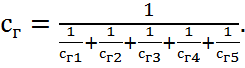                                                                                  (2.13)

Полученные результаты для отдельных участков трубопровода приведены в таблице 2.4

Таблица 2.4 – Параметры трубопровода гидросистемы

Параметр	Номер магистрали
	1	2	3	4	5
Площадь сечения трубопровода, Sтр, ·10-4 м2	0.785	1.767	1.767	1.767	1.767
Объем трубопровода, Vтр, ·10-4 м3	1.178	3.711	3.534	3.534	1.767
Доля объема трубопровода, Ψ	0.086	0.27	0.258	0.258	0.129
Коэффициент массы, mг, ·106 кг/м4	16.44	10.22	9.73	9.73	4.87
Коэффициент линейных потерь, μл, ·106 Н·с/м5	79.05	21.86	20.82	20.82	10.41
Коэффициент нелинейных потерь, μл, ·1010 Н·с/м5	52.73	14.05	12.39	12.39	6.885
Коэффициент жесткости участка, сг, ·1012 Н/м5	16.78	1.697	1.864	1.864	7.458

C_г=5.388*10¹¹ Н/м⁵.

2.6 Расчет статического режима работы гидросистемы

При постоянных внешних воздействиях система находится в установившемся равновесном состоянии. Её фазовые координаты при этом постоянны, такой режим функционирования системы называется статический. Статическое состояние гидросистемы достигается при постоянных внешних воздействиях.

1)Подачей насоса Pн1,Pн2.

2)Давлением потребителей Рв1,Рв2, Рв3.

При этом устанавливаются постоянные значения фазовых координат.

1)Расходы в жидкости гидромагистралей Q1, Q2, Q3, Q4, Q5.

2)Давление в упругих элементах Ру1.

Полагая 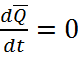 и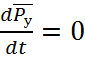, получим следующую систему нелинейных алгебраических элементов:

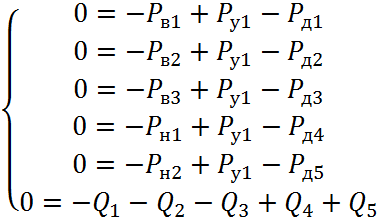                                                               (2.14)

Компонентное уравнение в диссипативных элементах в гидросистеме носят более сложный характер при этом выделяют линейные и нелинейные потери давления в гидромагистрали при этом их компонентные уравнения, запишутся виде:

, i =1..5                                                                                                 (2.15)

где  – коэффициент гидравлического сопротивления, характеризующий линейные потери при ламинарном режиме движения жидкости.

– коэффициент гидросопротивления характеризующий нелинейные потери при турбулентном режиме движения жидкости.

С учетом этого уравнения, преобразуем систему к следующему виду:

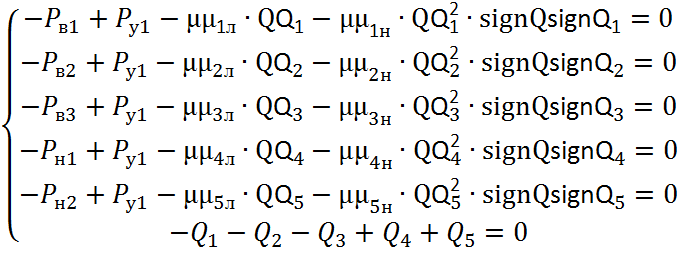                                                                                                 (2.16)

Полученная система уравнений является статической моделью системы, где в правой части известны значения входных воздействий. Для ее решения используется различные численные методы, для которых предварительно необходимо составить матрицу Якоби.

Матрица Якоби характеризует важнейшие свойства физической системы, а так же свойства уравнений математической модели, модель статического состояния гидросистемы, представляет собой систему нелинейных алгебраических уравнений вида: F(V) = 0                                                                                 

Элементами матрицы Якоби в этом случаи, являются частные производные от нелинейной вектор функции F(V) = (f₁,f₂ …f_n)  по фазовым коэффициентам системы (Q₁, Q₂, Q₃, Q₄,Q₅, Ру₁).

Для решения данной системы составим матрицу Якоби. Элементами матрицы Якоби являются частные производные по фазовым координатам.

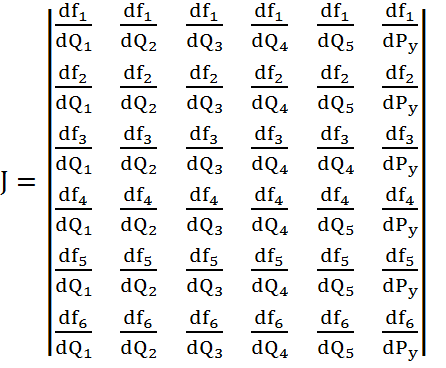                                                    (2.17)

В системе уравнений, нелинейной является функция P_дi=f(Q) , для них частные производные имеют вид:

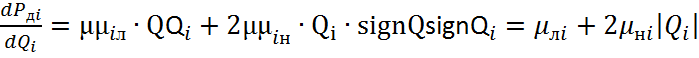                                         (2.18)

Тогда матрица Якоби, исследуемой гидросистемы, имеет вид:

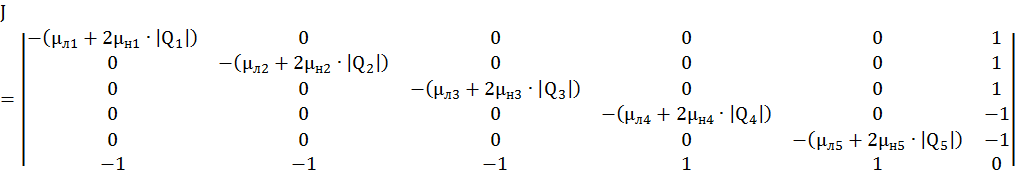
Для решения статической модели используем численный метод Ньютона, алгоритм которого включает следующие этапы:

-выбор начального приближения

где 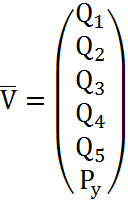       - вектор фазовых координат,                                       (2.19)

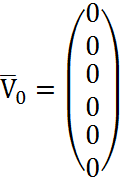             – нулевой вектор-столбец.                                            (2.20)

-вычисление матрицы Якоби J_k в точке  (k=0, 1, 2, 3…);

-вычисление вектора невязок . Вектор невязок получается из системы уравнений (2.16) для статического режима:

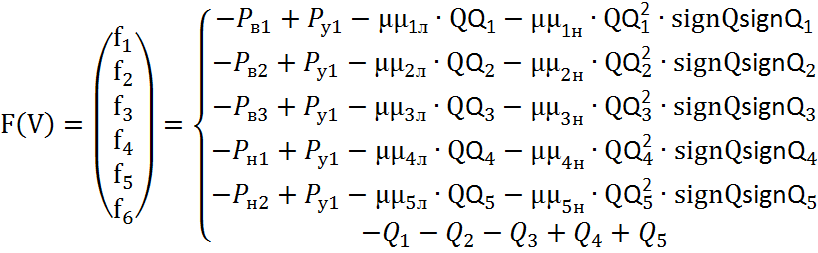                      (2.21)

-определение вектора поправок:

.                                                                                     (2.22)

-определение нового приближения вектора искомых фазовых координат:

.                                                                                      (2.23)

-проверка условия окончания итерационного процесса.

Если V_k и V_k+1 соизмеримы (совпадают до десятых долей) процесс завершается, иначе происходит переход на второй этап.

Расчёт фазовых координат для статического режима произведён в математическом пакете MathCad.

Результаты вычислений представлены в таблице 2.5

Таблица 2.5 – Результаты статического анализа

Фазовые координаты	Pн1=0.2*10-6 м3/c Pн2=0*10-6 м3/c	Pн1=0.2*10-6 м3/c Pн2=0.2*10-6 м3/c
Q1, м3/c	-1.205*10-15	0
Q2, м3/c	-1.154*10-15	2.354*10-15
Q3, м3/c	-3.133*10-15	0
Q4, м3/c	4.573*10-15	0
Q5, м3/c	-1.006*10-14	1.78*10-15
Ру, Па	1.05*10-7	1.815*10-7

2.7 Анализ динамических свойств гидросистемы

Динамическая модель описывает переходный процесс гидроситемы. В общем случае система дифференциальных уравнений, описывающих гидравлическую систему имеет вид: