Содержание
1. Параметры элементов эквивалентной схемы объекта управления….1
2.Построение математической модели ОУ
в пространстве состояния……………………………………………………..2
3.Составление структурной схемы ОУ и сигнального графа……………..5
4.Нахождение передаточной функции с использованием формулы
Мейсона…………………………………………………………………………..6
5.Нахождение импульсной и переходной характеристик
по передаточной функции
построение графиков реакции ОУ на единичные импульсный и
ступенчатый сигналы
расчет и построение амплитудной и фазовой
частотных характеристик ОУ……………………………………………….11
6.Нахождение переходной и импульсной характеристик ОУ
по математической модели в пространстве состояния с
использованием формулы Коши……………………………………………14
 |
Параметры элементов эквивалентной схемы объекта управления
R1=346 Ом
R2=405 Ом
R3=109 Ом
R4=198Ом
R5=46 Ом
L1=27 Гн
L2=22 Гн
C=37919 мкФ
Входной сигнал U
Выходной сигнал i1
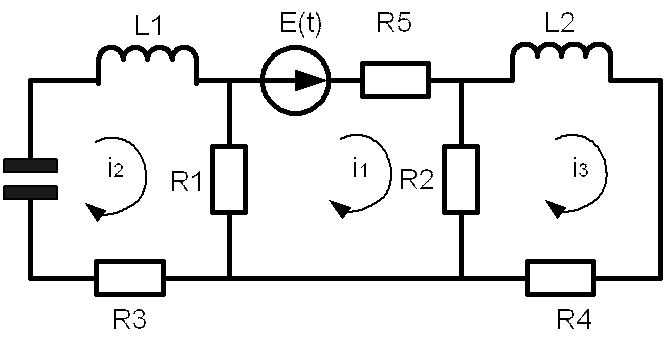
Рис 1. Эквивалентная схема объекта управления
![]()
![]()
|
Структурная схема объекта управления
1.Построение математической модели ОУ в пространстве состояния
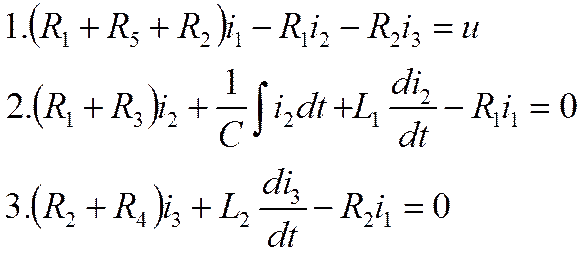
Во втором уравнении есть интеграл, поэтому дифференцируем его
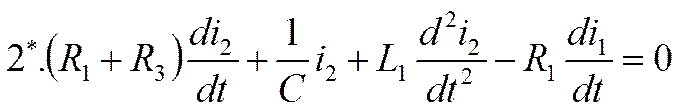
Берем уравнение 2*, в котором есть уравнение второго и первого порядка
и в качестве Х1 выбираем элементы данного уравнения с производными на
один порядок ниже
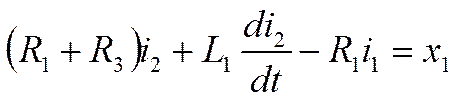
Вводим вектор Х2 по тому же принципу
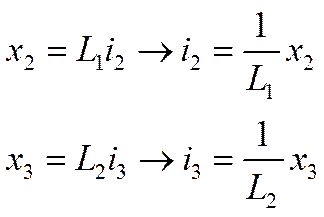
Уравнение в пространстве состояний записывается в левой части
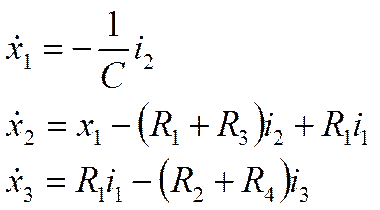
В данном уравнении имеется 6 переменных i1, i2, i3, x1x2x3
необходимо уйти от i1, i2, i3 выразив их через xi
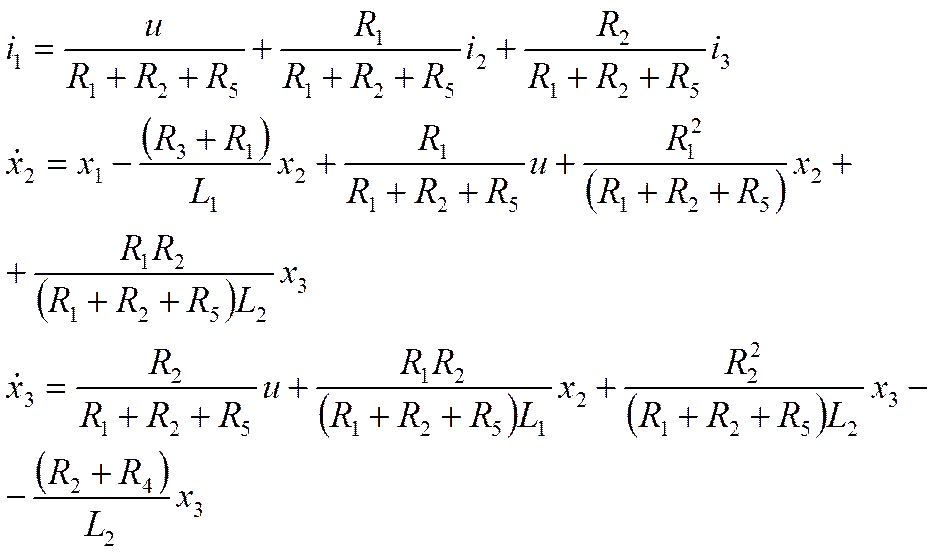
Теперь имеем выраженные выражения в зависимости от i1, i2, i3
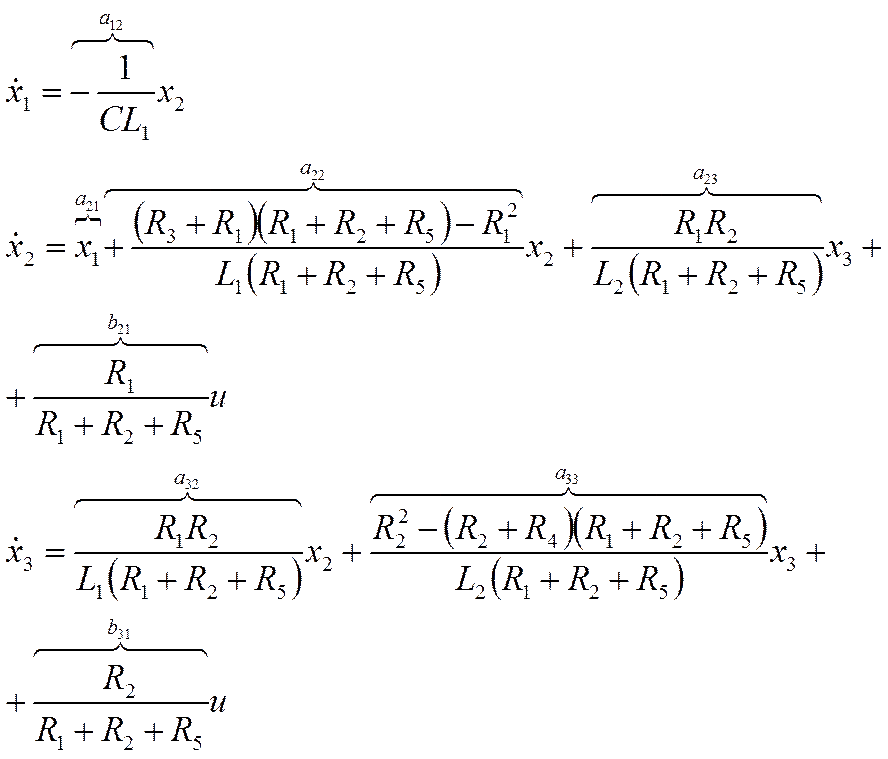
Получим
3 д.у. 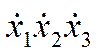 и одно уравнение выходного порядка.
и одно уравнение выходного порядка.
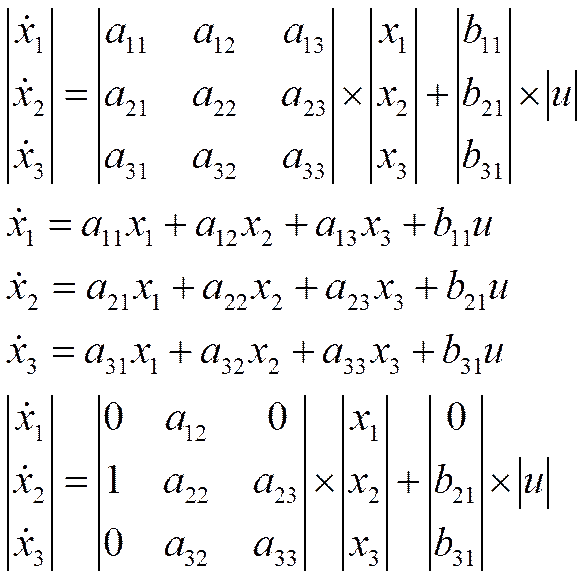
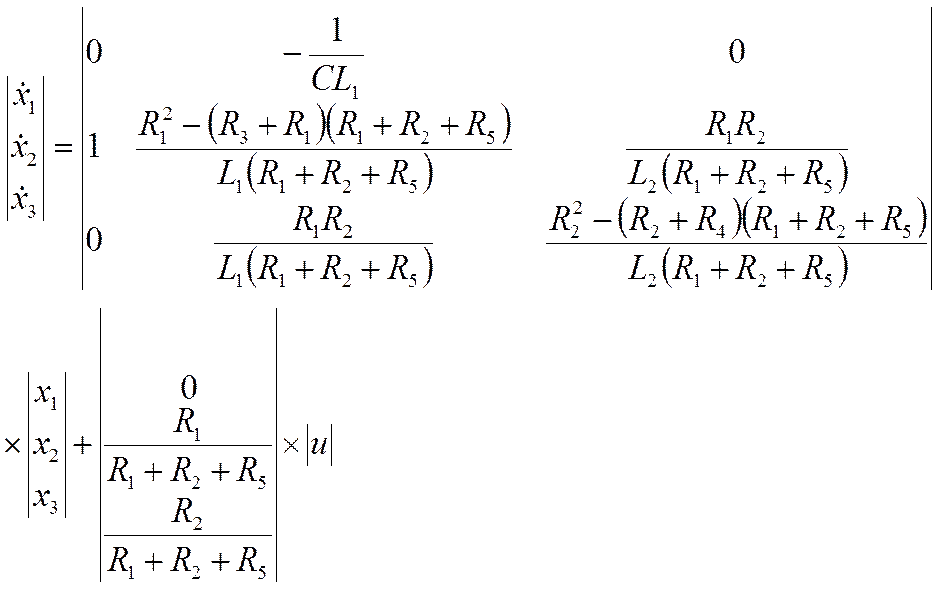
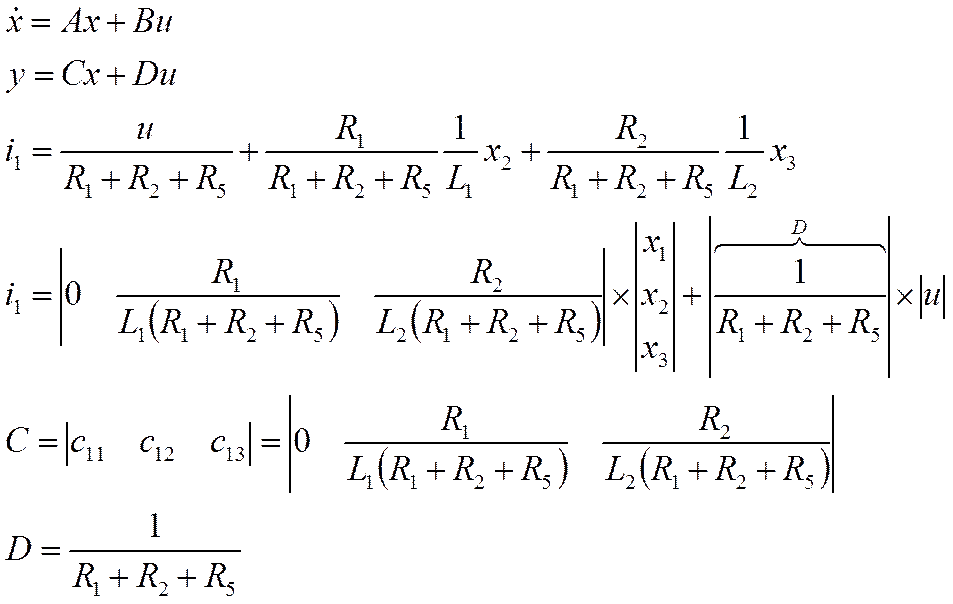
2.Построение сигнального графа и структурной схемы
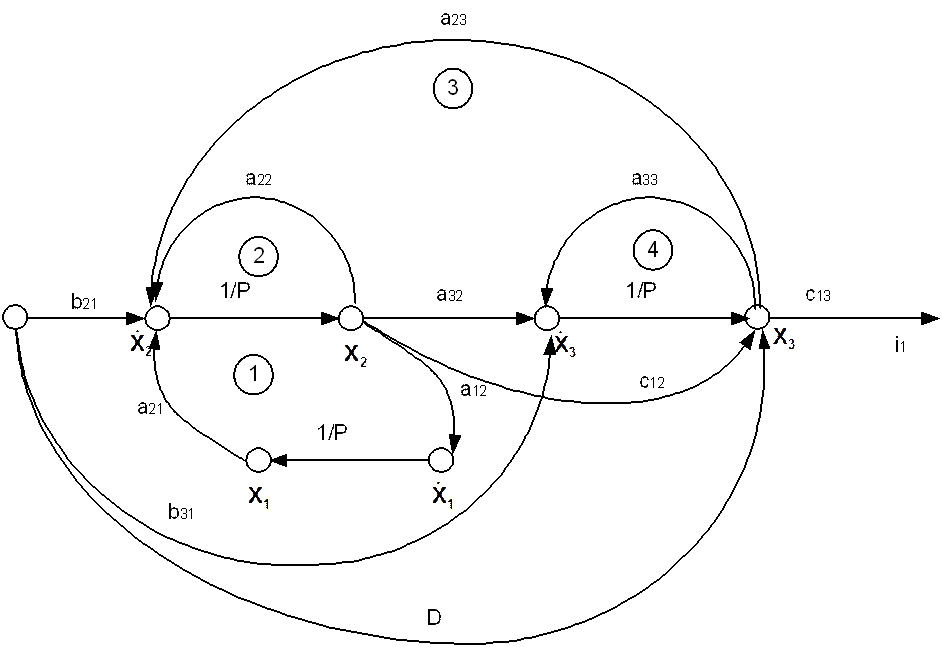
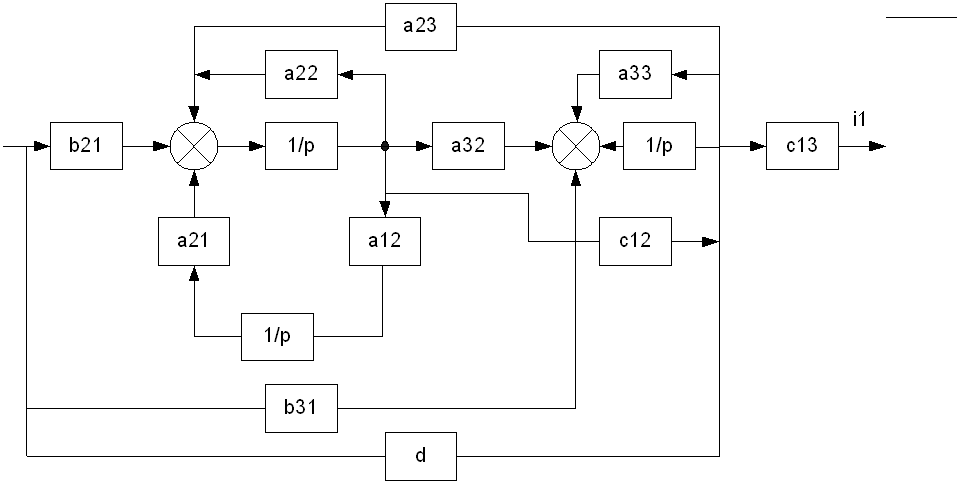
3.Построение передаточной функции ОУ с использованием формулы
Мейсона
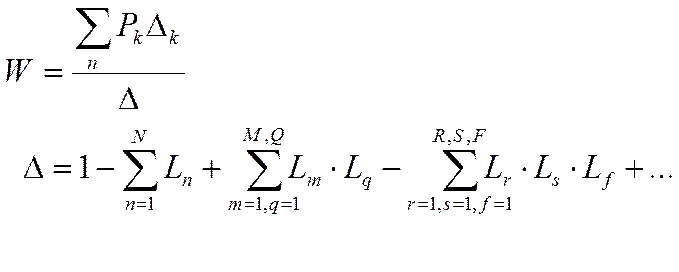
![]() - количество возможных путей от входа
к выходу,
- количество возможных путей от входа
к выходу,
![]() - определитель графа,
- определитель графа,
 - коэффициент передачи
- коэффициент передачи ![]() ого пути от входа к выходу,
ого пути от входа к выходу,
![]() - определитель всех касающихся
контуров при удалении
- определитель всех касающихся
контуров при удалении ![]() ого пути,
ого пути,
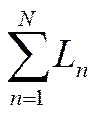 -
сумма коэффициентов передачи всех отдельных контуров,
-
сумма коэффициентов передачи всех отдельных контуров,
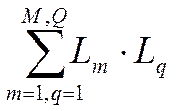 -
сумма всех возможных произведений из 2ух некасающихся
-
сумма всех возможных произведений из 2ух некасающихся
контуров
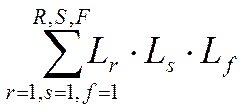 - сумма всех возможных комбинаций из 3ох
некасающихся
- сумма всех возможных комбинаций из 3ох
некасающихся
контуров
Последовательность нахождения передаточной функции по формуле
Мейсона.
1.Определить и записать уравнения всех ![]() путей от входа к
путей от входа к
выходу:![]() .
.
2. Выявить число замкнутых контуров и
записать их уравнения: ![]() .
.
3. Записать выражение для определителя
системы ![]() .
.
4.Записать сомножители: ![]() .
.
5.Записать и преобразовать выражение
передаточной функции ![]() .
.
Данная система имеет четыре пути от входа к выходу
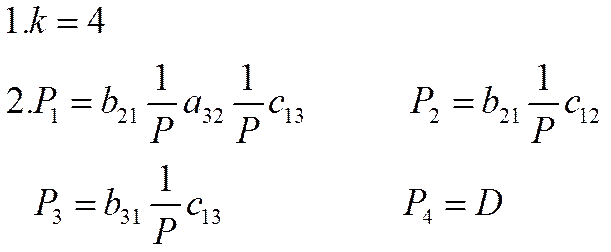
В системе имеются 4 замкнутых контура и две пары некасающихся
контуров
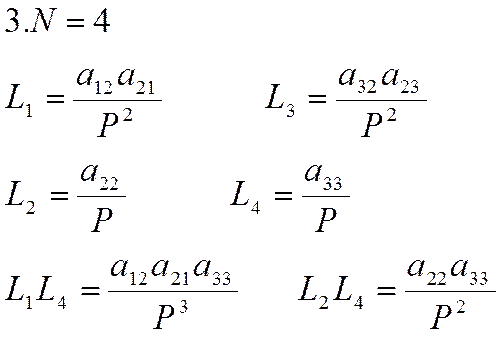
![]()
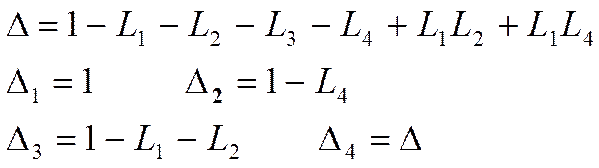
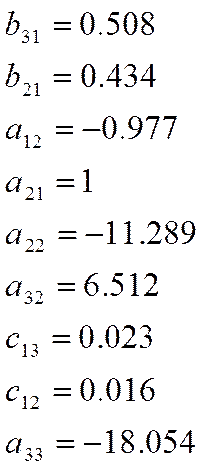
![]()
После подстановки коэффициентов передаточная функция имеет вид:
![]()
4. Найдем весовую и переходную характеристики для полученной
передаточной функции.
Построение весовой функции.
Представим передаточную функцию в виде:
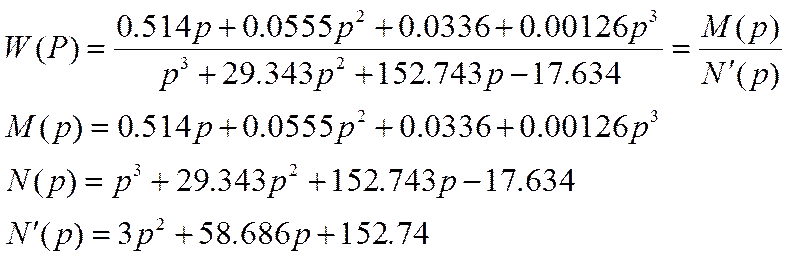
Найдем
корни характеристического уравнения ![]() .
.
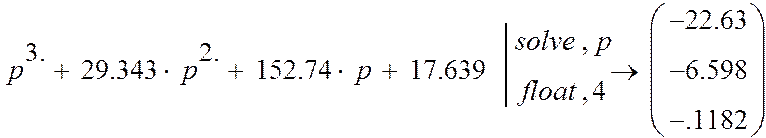
![]()
Рассчитаем компоненты импульсной функции.
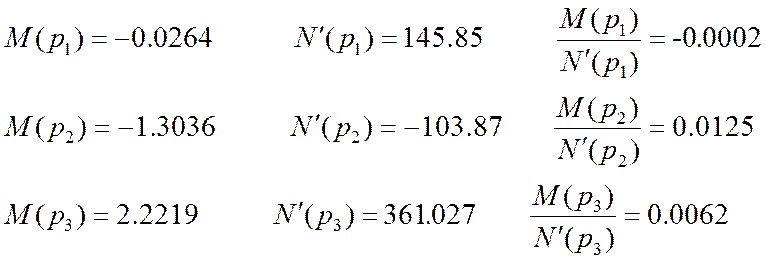
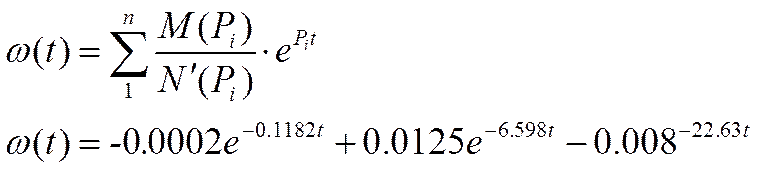
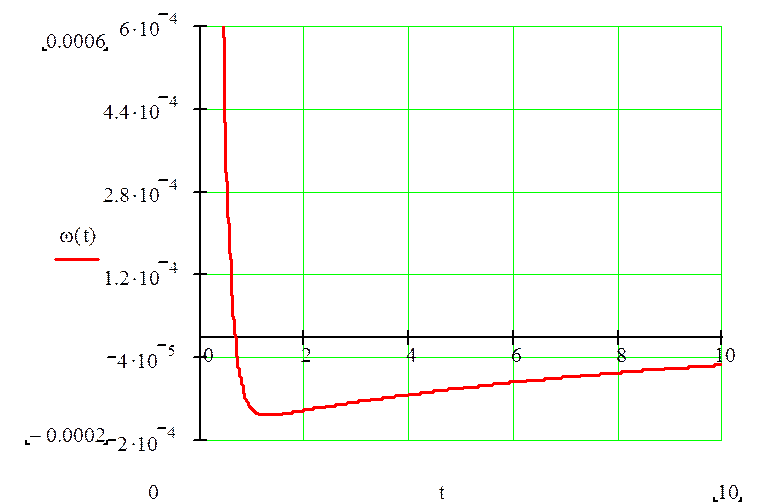
график весовой функции
Построение переходной функции.
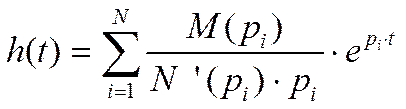
Рассчитаем компоненты переходной функции
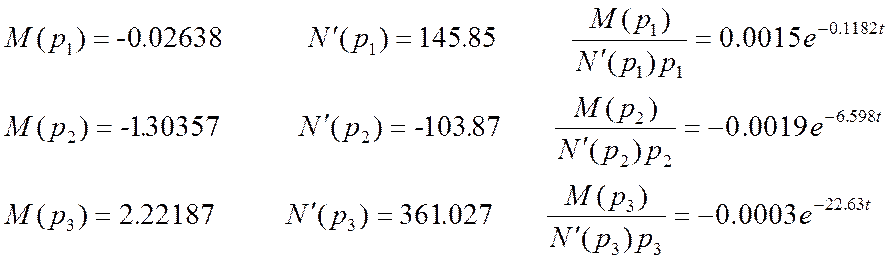
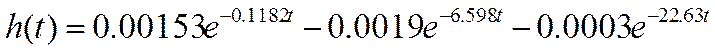
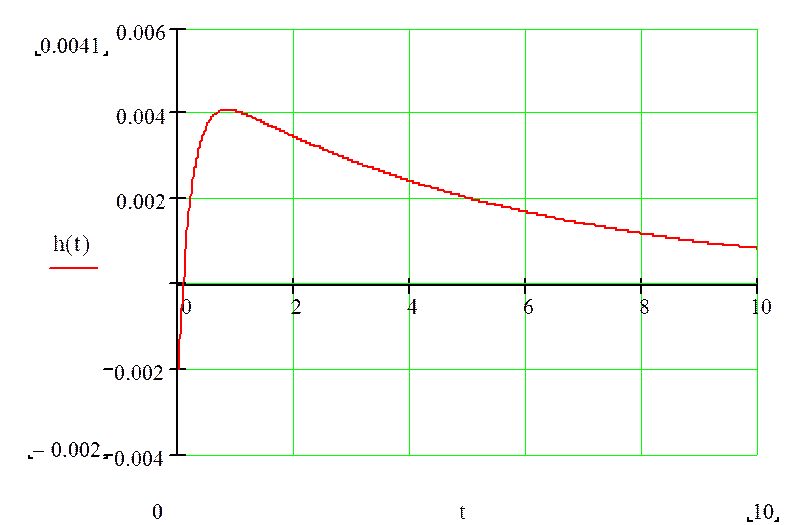
График переходной функции
Рассчитаем производную переходной характеристики:
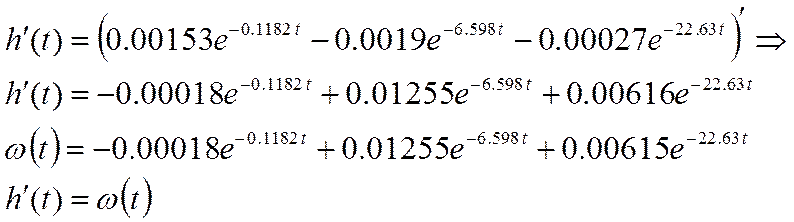
Получили выражение, которое совпадает с весовой характеристикой,
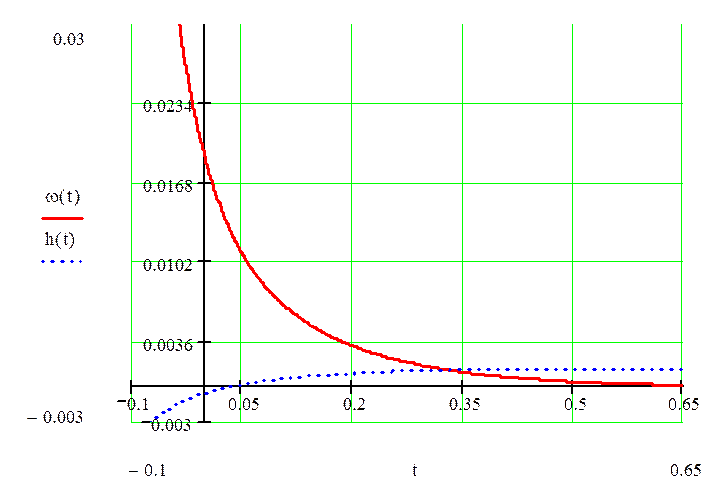
следовательно расчет выполнен верно. Совместим графики весовой и
переходной характеристик.
5. Рассчет и построение графиков
амплитудно-частотной, амплитудно-фазовой характеристик.
Последовательность нахождения частотных характеристик
1)Сделать замену в передаточной
функции ![]() .
.
2)Освободимся от мнимых чисел в знаменателе путем умножения
числителя на комплексно-сопряженно знаменателю число
3)Раскрыть скобки и привести подобные члены и разделить в числителе
на сумму вещественного и мнимого полиномов.
4)Записать выражения для вещественной ![]() и мнимой
и мнимой ![]() частотных
частотных
характеристик.
5)Записать выражения для амплитудно-частотной и амплитудно-фазовой
характеристик.
6) Построить графики
Построение частотных характеристик по полученной передаточной
Функции
Ручной расчет по передаточной функции
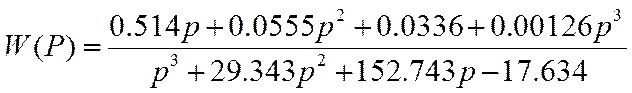
Найдем корни
характеристического уравнения ![]() .
.
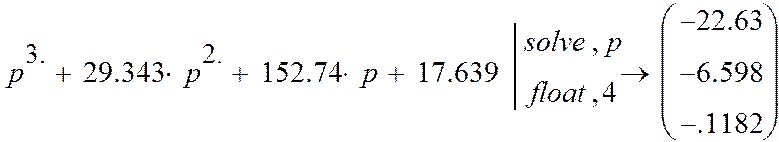
Тогда передаточная функция примет вид:
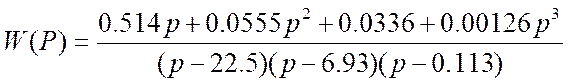
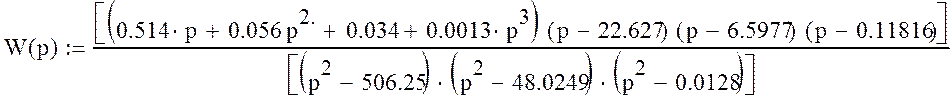
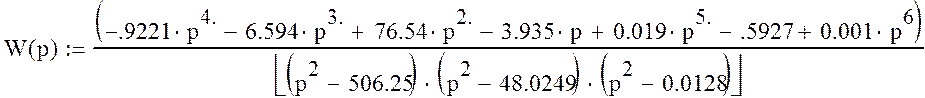
После раскрытия скобок, приведения подобных и разделения вещественной
и мнимой частей получаем:
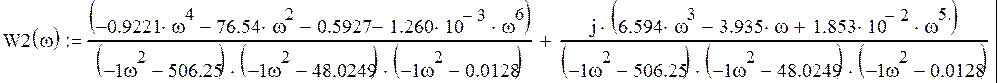
Запишем выражения для вещественной ![]() и мнимой
и мнимой ![]() частотных
частотных
характеристик.
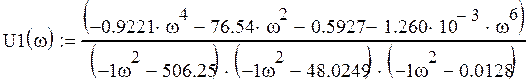
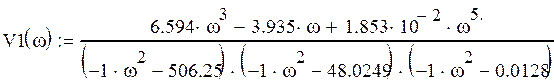
Запишем выражения для амплитудно-частотной и амплитудно-фазовой
характеристик.
![]()
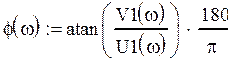
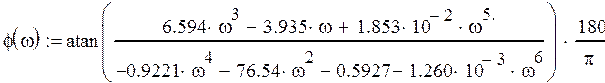
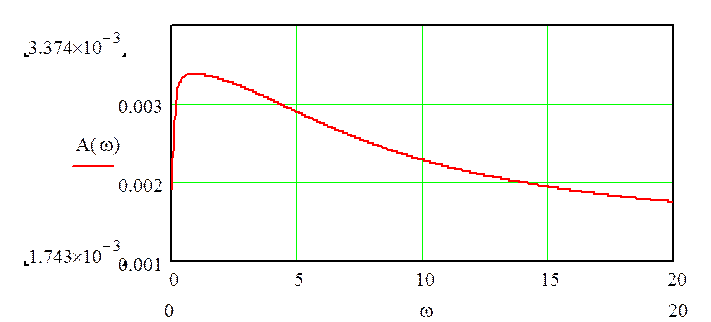
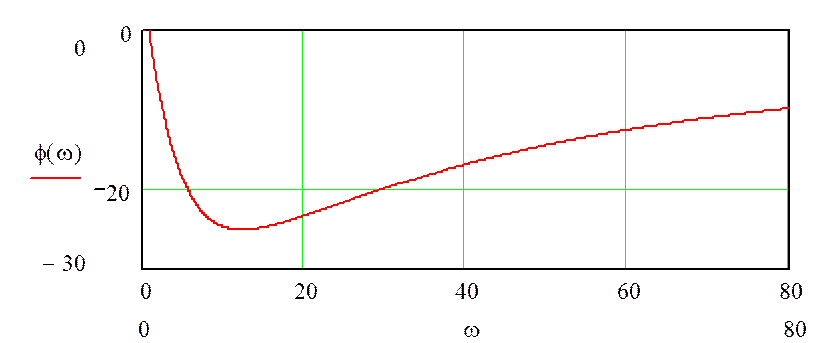
график фазовой характеристики
6.Нахождение переходной и импульсной характеристик ОУ по мат.модели
в пространстве состояния с использованием формулы Коши
Решение уравнения Коши при ступенчатом и импульсном входе. Решение
ур-я Коши имеет вид при нулевых начальных условиях первый член равен 0
Нахождение матричной переходной функции производим по формуле
Лагранжа-Сильвестра
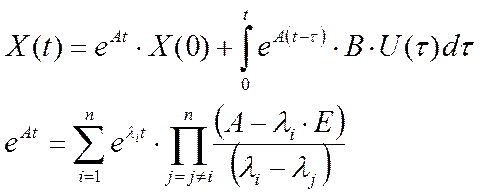
Ввод параметров матрицы А
![]()
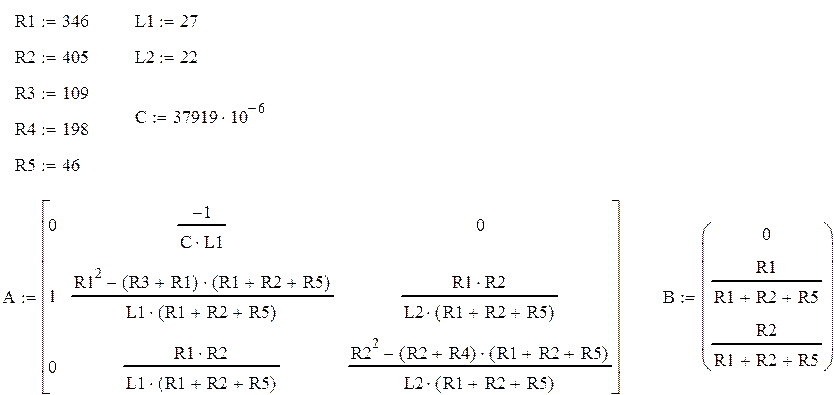
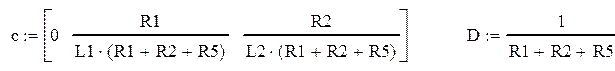
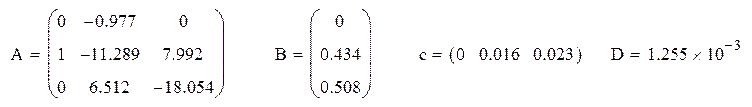
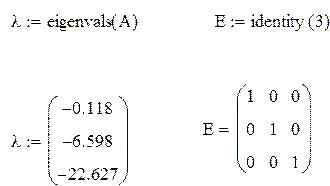
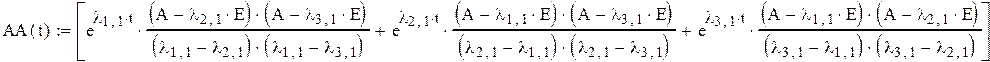
В данном случае матрица В не зависит от времени и U(t)=1.
Подинтегральное выражение равно
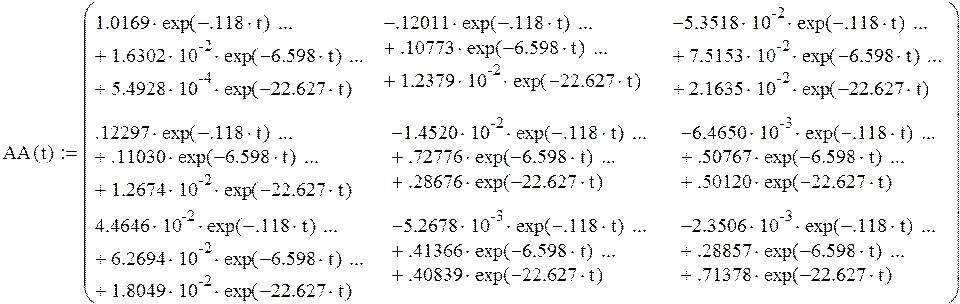
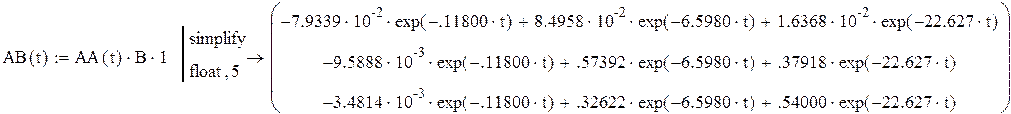
Матрицы в Mathcad не интегрируются и не дифференциируются. Поэтому
надо интегрировать отдельно элементы матриц. Нам необходимо найти
выражение для:
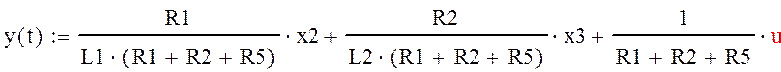
поэтому далее используем только строку для
![]()
![]()
Интегририруем выражение решения уравнения Коши для переменной
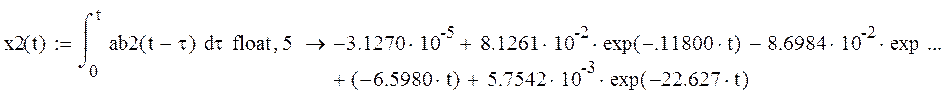
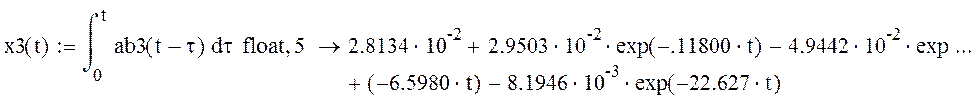
Находим выходную переменную через элементы матриц C и D
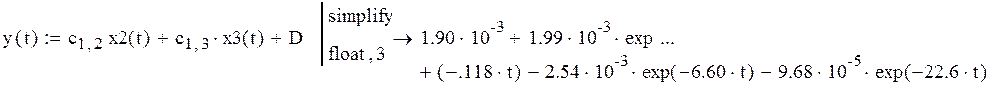
Решение совпадает с решением, полученным вручную
![]()
Весовую функцию сейчас найдем путем дифференцирования переходной
характеристики
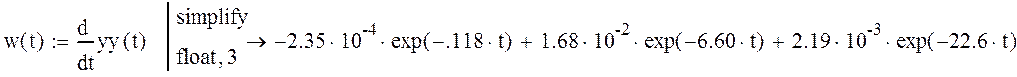
![]()
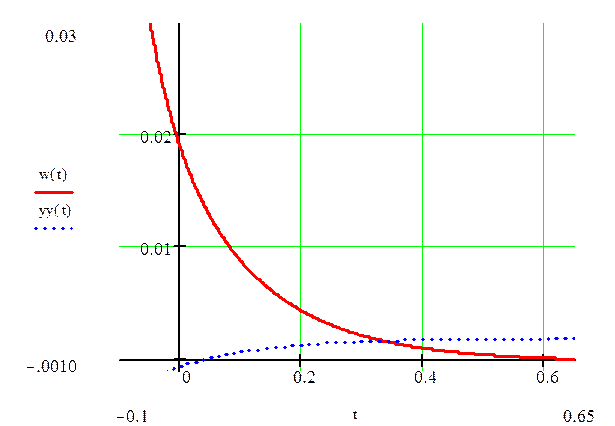
7.Расчет и построение графиков амплитудной и фазовой частотных
характеристики в MathCad
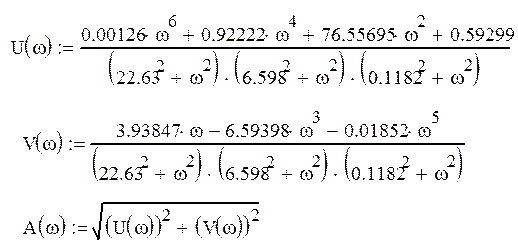
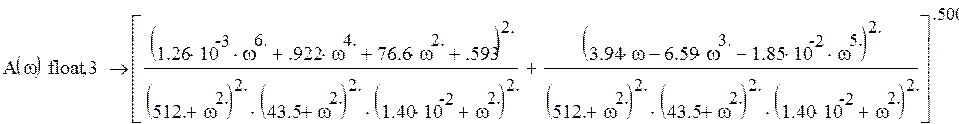
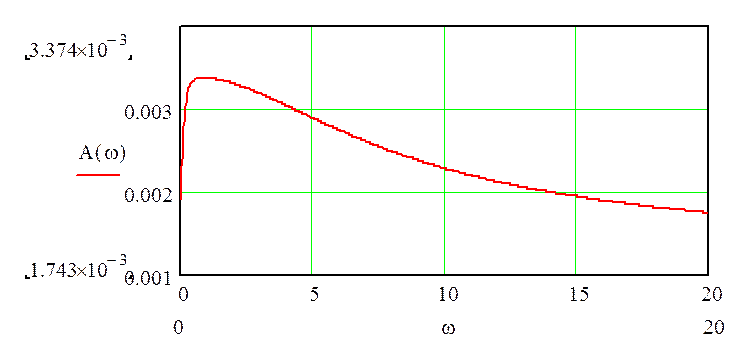
график амплитудной характеристики
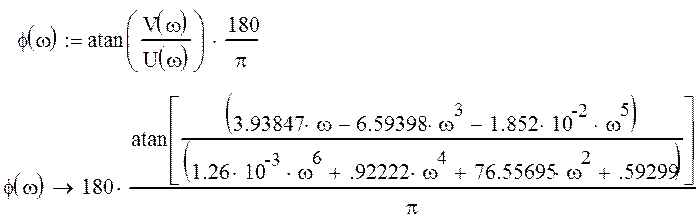
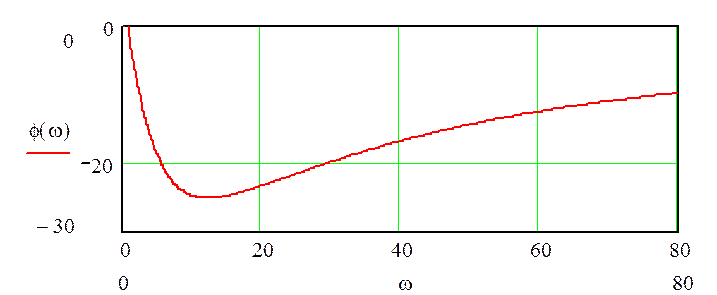
график фазовой характеристики
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.