Построение и анализ математической модели объекта управления

Министерство высшего и профессионального образования РФ

Саратовский государственный технический университет

Балаковский институт техники технологии и управления

Кафедра УИТ

Курсовая работа

по курсу:

«Математические основы теории систем»

Построение и анализ математической модели объекта управления

Выполнил: ст. гр УИТ 42В

Проверил преподаватель

Балаково 2003 г.

Задание

 

№ варианта	Параметры элементов эквивалентной схемы объекта управления										Выходная переменная
15	R1 Ом	R2 Ом	R3 Ом	R4 Ом	R5 Ом	L1 Гн	L2 Гн	L3 Гн	C1 МкФ	C2 мкФ	I3
	335	389	114	219			20	50		17180

Эквивалентная схема объекта управления

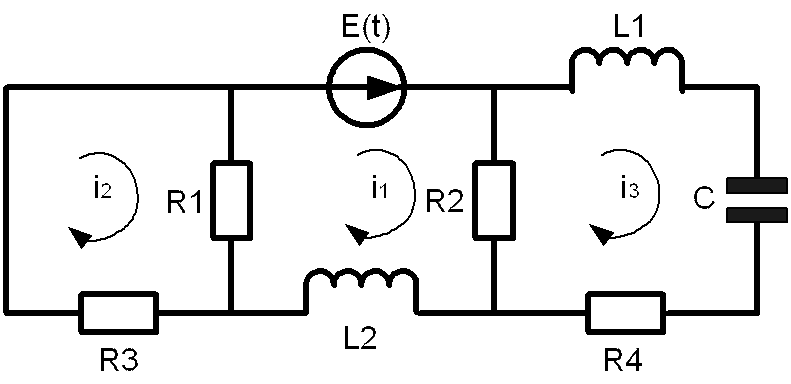
В схеме три элемента, запасающих энергию, следовательно, математическая модель должна быть 3-го порядка.

          При построении математических моделей следует учитывать следующие выражения для связи токов, напряжений и комплексных сопротивлений элементов электрической схемы.

Для сопротивления R                                                                                                      

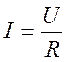
Для индуктивности L                                       

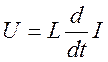
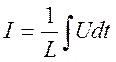
Для емкости C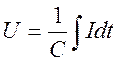

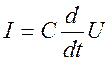
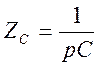
 1 часть

1.Построение математической модели ОУ в пространстве состояния.

Задаемся направлением контурных токов i1,i2,i3

Составляем 3 уравнения по 2-му закону Кирхгофа для контуров

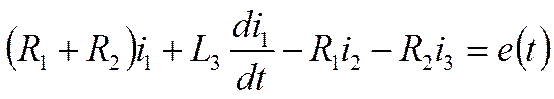
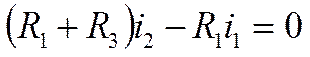
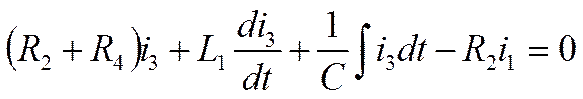
В третьем уравнении есть интеграл, поэтому дифференцируем его

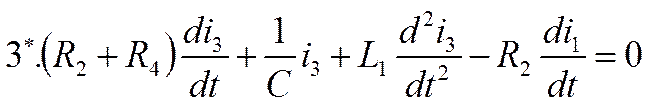
Берем уравнение 3^*, в котором есть уравнение второго и первого порядка и в качестве Х1 выбираем элементы данного уравнения с производными на один порядок выше

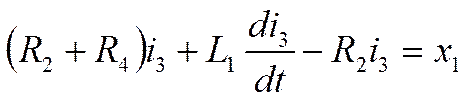
Вводим вектор Х2 по тому же принципу

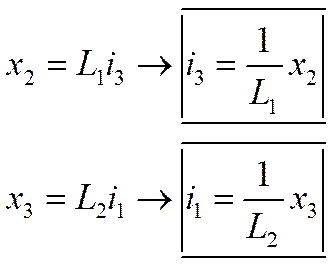
Уравнение в пространстве состояний записывается в левой части

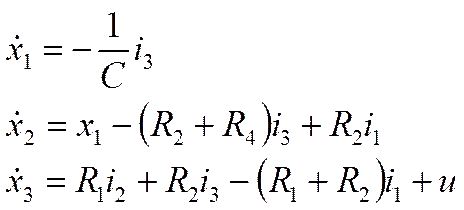
В данном уравнении имеется 6 переменных i₁, i₂, i₃, x₁x₂x₃ 

необходимо уйти от i₁, i₂, i₃  выразив их через x_i

Из 1-го уравнения

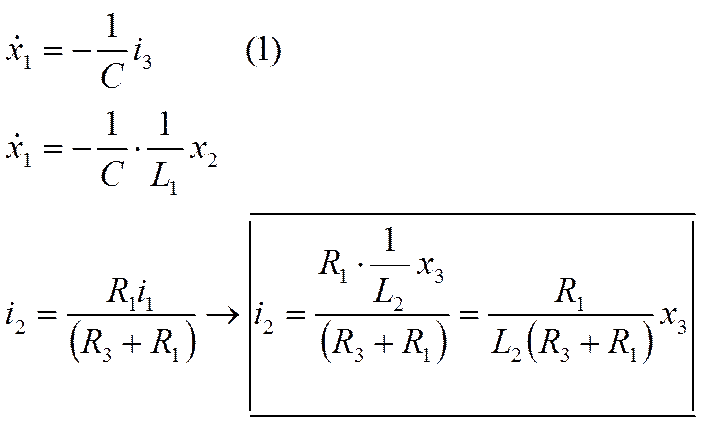
Теперь имеем выраженные выражения в зависимости от i₁, i₂, i₃

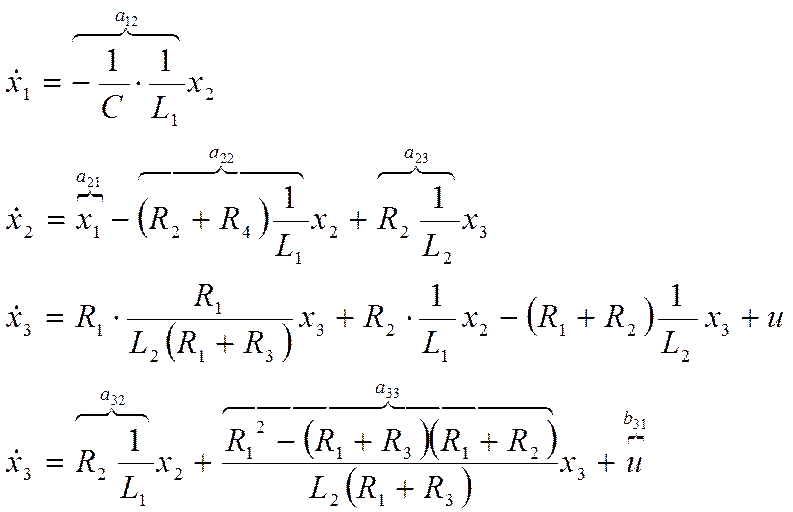
Получим 3 дифференциальных ур. 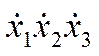и одно уравнение выходного порядка.

Запишем полученную систему дифференциальных уравнений в матричном виде

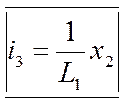
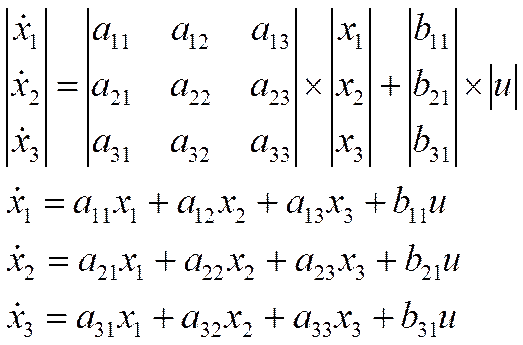
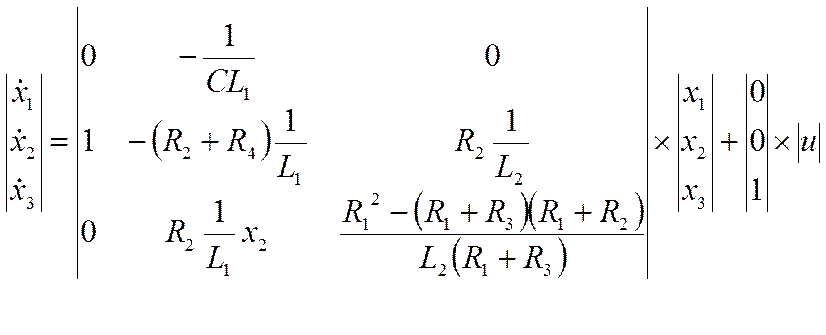
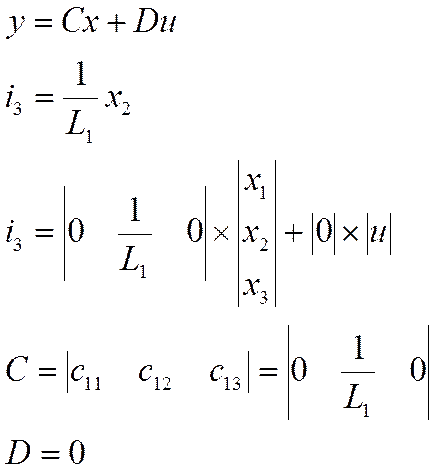
2.Построение структурной схемы и сигнального графа

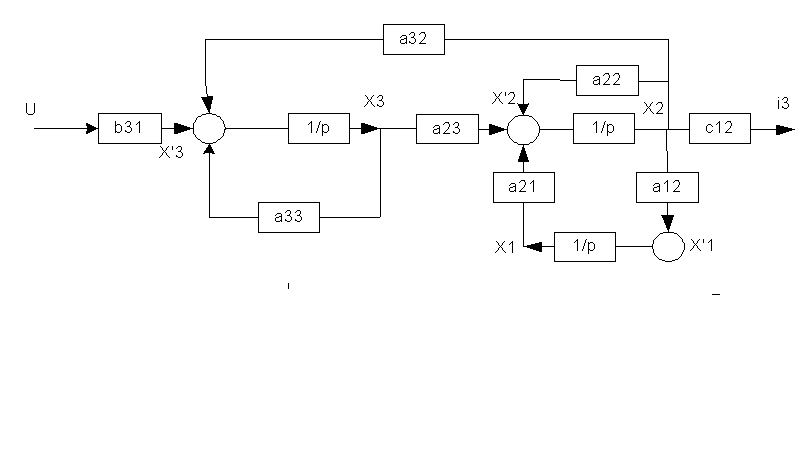
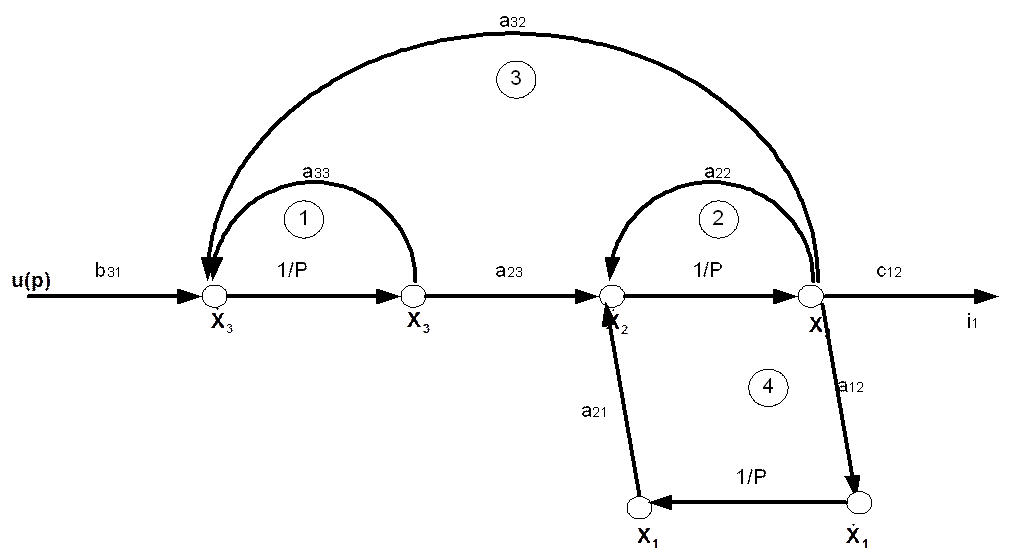
3.Построение передаточной функции ОУ с использованием формулы Мейсона

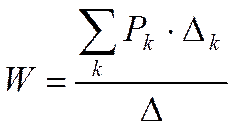
k- количество возможных путей от входа к выходу,

D-определитель графа

Pk-коэффициент передачи k-го пути от входа к выходу

Dk- определитель всех касающихся контуров при удалении k-го пути

D=1- (сумма коэффициентов передачи всех отдельных контуров) +(сумма всех возможных произведений из 2-х некасающихся контуров)- (сумма всех возможных комбинаций из 3-х некасающихся контуров)+      +

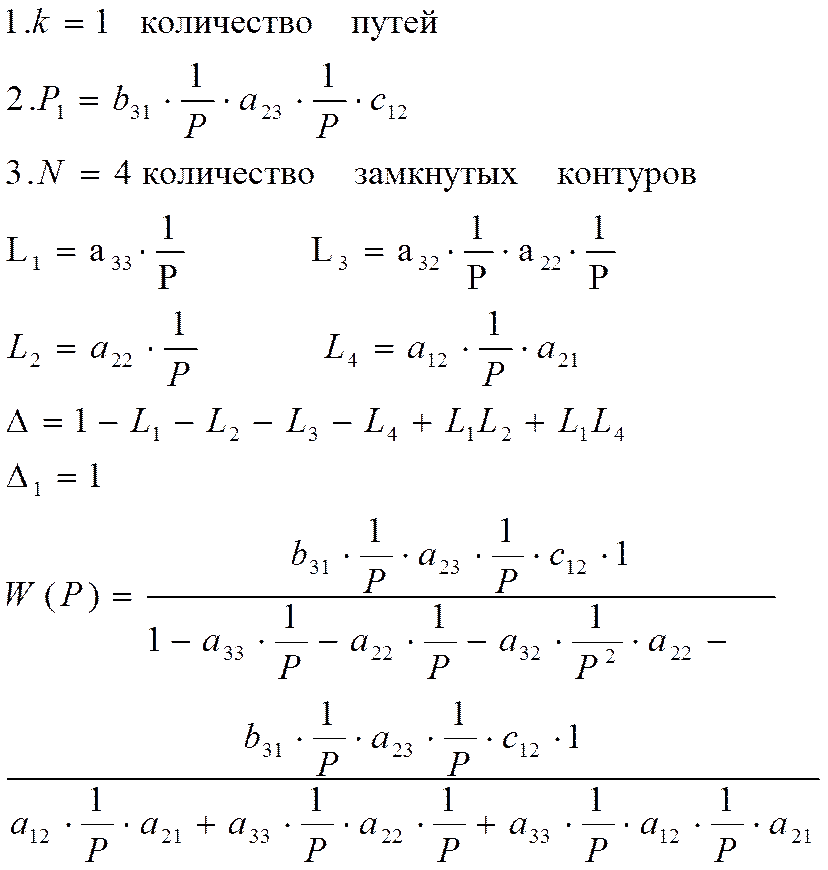
4. По полученной передаточной функции найти выражения для весовой и переходной характеристик и построить их графики.

После подстановки значений коэффициентов передаточная функция имеет вид:

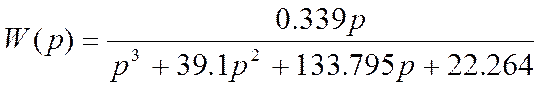
В знаменателе имеем характеристическое уравнение 3 порядка

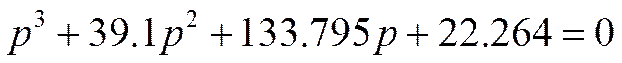
Решив это уравнение, получим 3 отрицательных корня

P₁=-35.33

P₂=-3.59

P₃=-0.175

Тогда передаточная функция будет иметь вид:

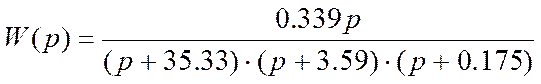
По полученной передаточной функции найдем выражения для весовой и переходной характеристик и построим их графики.

1. Построение весовой характеристики системы.

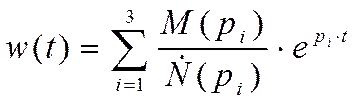
M(p_i)=0.339p

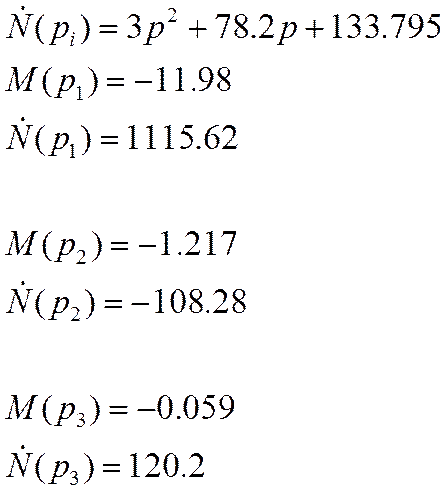
Весовая характеристика будет иметь вид:

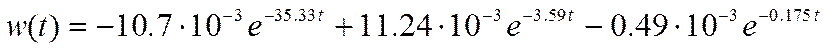
2.Построение переходной характеристики системы.

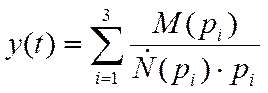
В таком случае переходная характеристика будет иметь вид:

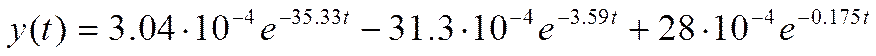
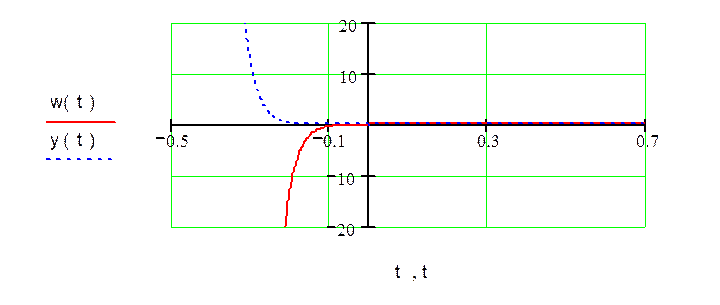
Построим  графики весовой и переходной характеристик

3. Рассчитать и построить графики амплитудной и фазовой частотных характеристик.

                        

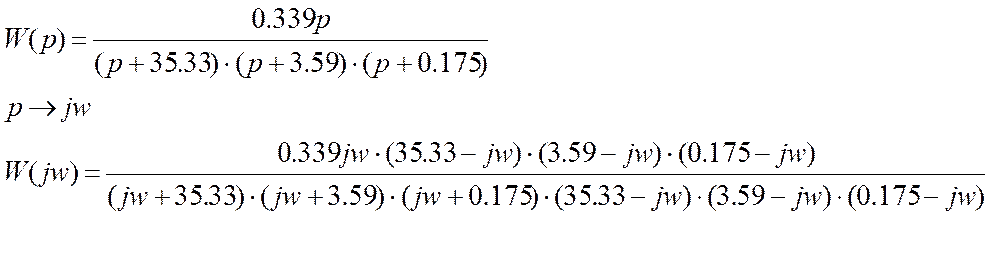
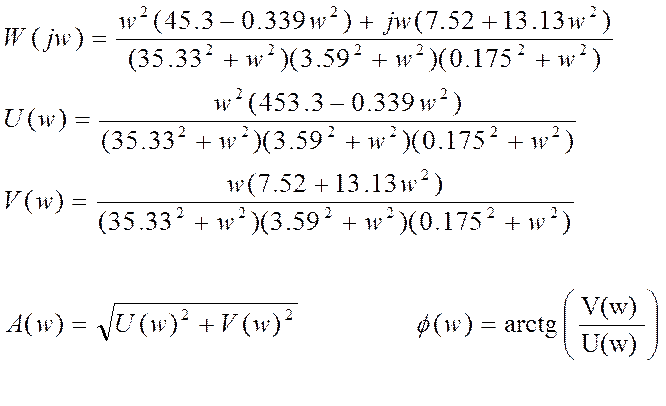После перемножения скобок, приведения подобных членов и разделения вещественной и мнимой частей получаем:

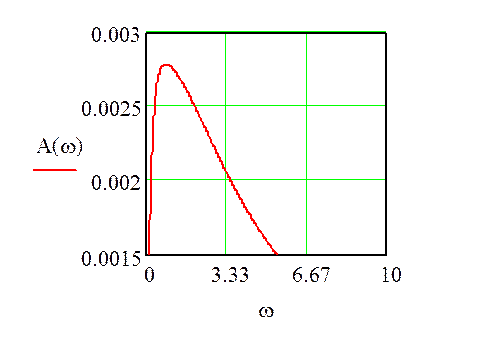
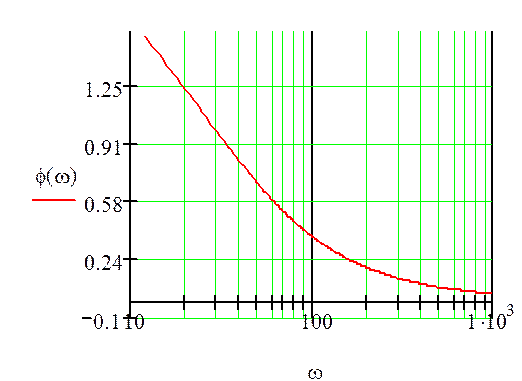
2 часть

По полученной в 1 части передаточной функции найдем амплитудную и фазовую частотные характеристики и весовую и переходную функции.

 

            

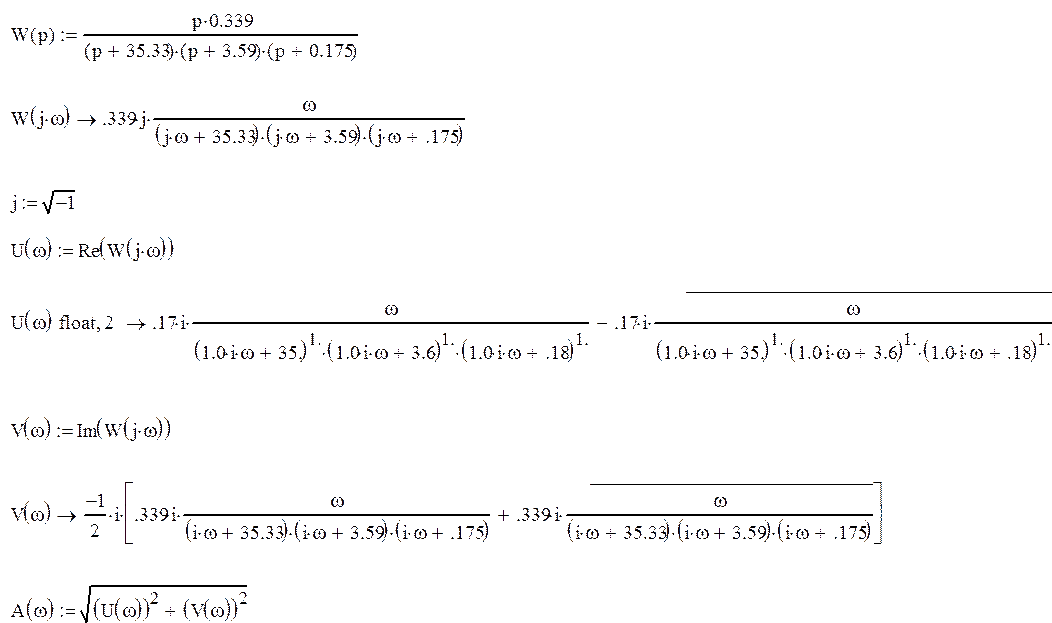
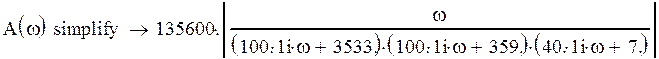
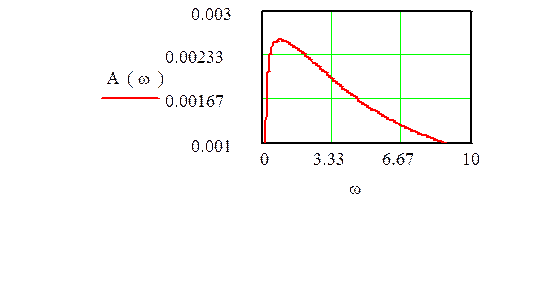
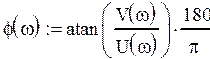
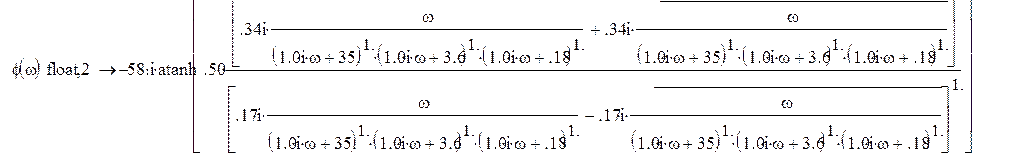
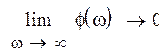
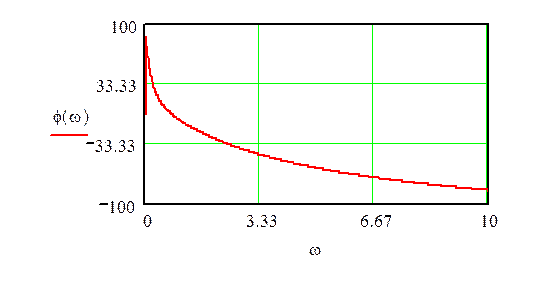
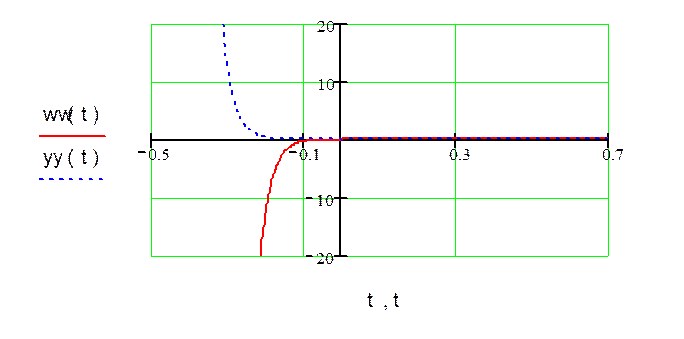
Построим графики весовой и переходной функций.

 

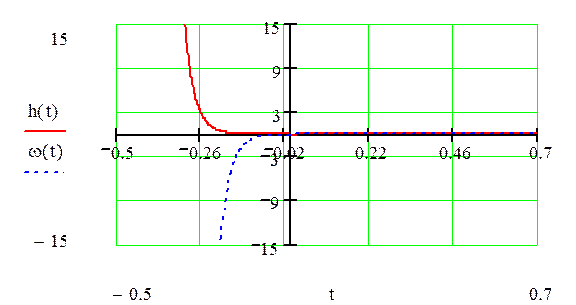
Математическая модель электрической схемы в пространстве параметров.

Решение уравнения Коши при ступенчатом и импульсном входе. Решение уравнения Коши имеет вид:

 

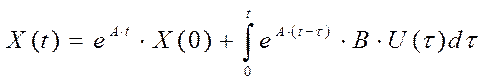
При нулевых начальных условиях первый член равен 0. Нахождение матричной переходной функции производим по формуле Лагранжа-Сильвестра:

 

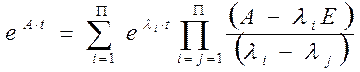
Введем параметры матрицы А:

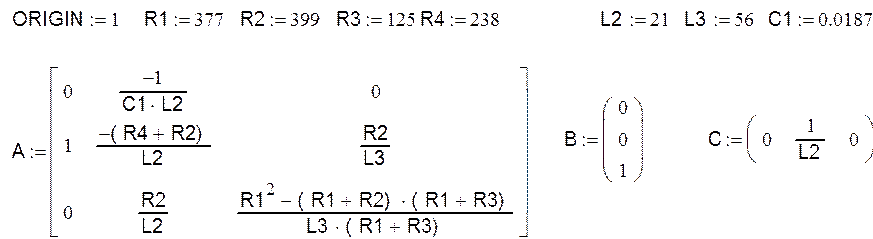
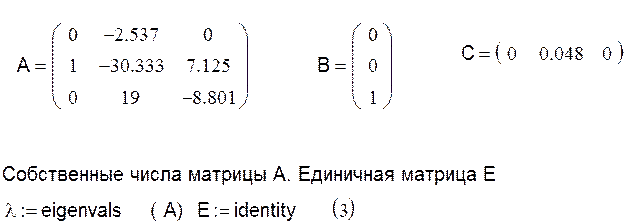
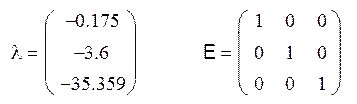
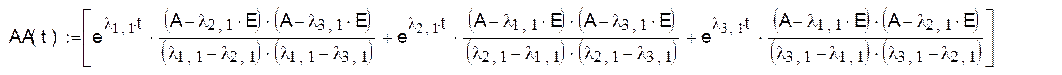
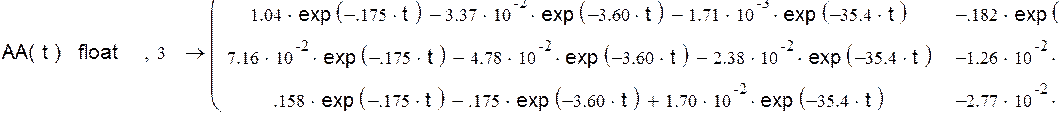
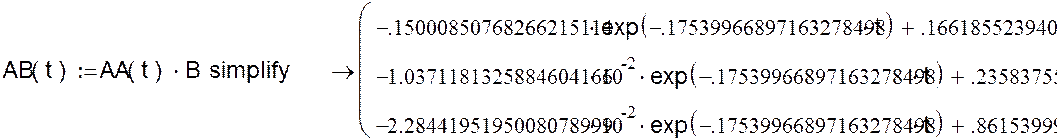
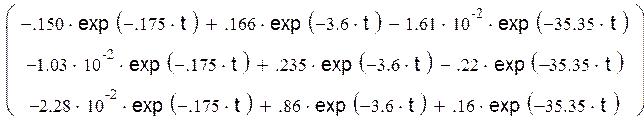
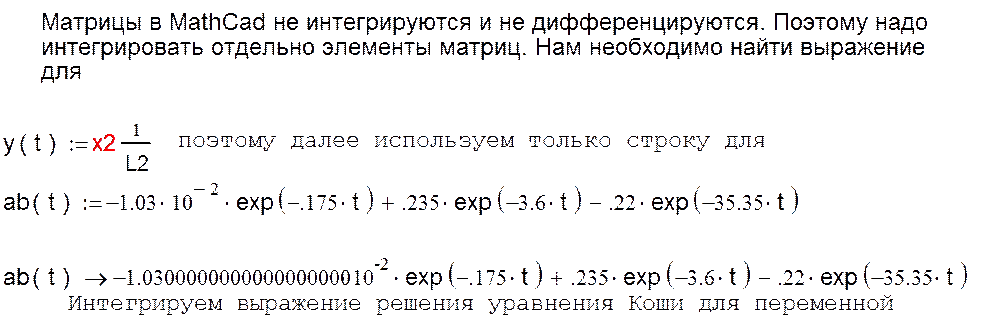
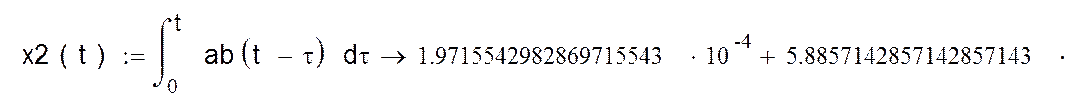
Переобозначим и перезапишем, чтобы уместить на одной строке

Находим выходную переменную через элементы матриц C и D

                                                                                          

Переобозначим и перезапишем, чтобы уместить в одной строке

Решение совпадает с решением, полученным в ручную

Содержание:

Задание……………………………………………………………………………………………………..2

1 часть

1. Построение математической модели ОУ в пространстве состояния……………………3
2. Составление структурной схемы и сигнального графа…………………………………….6
3. Построение передаточной функции ОУ, используя формулу Мейсона………………...7
4. Нахождение весовой и переходной хар-к, амплитудной и фазовой частотных хар-к...8

2 часть

1. Построение в Mathcad весовой и переходной хар-к, амплитудной и фазовой

 частотных хар-к………………………………………………………………………………………..11

2. Нахождение переходной и весовой хар-к, используя формулу Коши……………………..13

 

Содержание:

Задание……………………………………………………………………………………………………..2

1 часть

5. Построение математической модели ОУ в пространстве состояния……………………3
6. Составление структурной схемы и сигнального графа…………………………………….6
7. Построение передаточной функции ОУ, используя формулу Мейсона………………...7
8. Нахождение весовой и переходной хар-к, амплитудной и фазовой частотных хар-к...8

2 часть

2. Построение в Mathcad весовой и переходной хар-к, амплитудной и фазовой

 частотных хар-к………………………………………………………………………………………..11

2. Нахождение переходной и весовой хар-к, используя формулу Коши……………………..13