Нижегородский государственный технический университет
Кафедра “Теория автоматического управления”
Курсовая работа № 1 по курсу
“Теория автоматического управления”
Вариант 5-5
Выполнил: студент гр. 97-ЭПА-2
Крацер А.А.
Принял: Шахов А.В.
Нижний Новгород
1999 г.
Содержание.
Исходные данные. Структурная схема системы .................
1. По структурной схеме получить систему уравнений динамики в оригиналах для динамических звеньев и сумматоров. Определить тип динамических звеньев..........
2. Рассчитать и построить амплитудно-фазовые характеристику, л.а.ч.х., л.ф.ч.х., переходную функцию пятого звена.......................................................................................
3. По структурной схеме САР получить передаточную функцию разомкнутой по цепи главной обратной связи системы, а также передаточные функции замкнутой системы для регулируемой величины и ошибки по задающему воздействию.........................................................................
4. Проверить замкнутую систему на устойчивость с корректирующей обратной связью и без нее. Определить значения критических коэффициентов усиления в обоих случаях.................................................................................
5. Построить логарифмические частотные характеристики разомкнутой системы с корректирующей внутренней обратной связью. Определить запасы устойчивости по модулю и фазе......................................................................................
6. Рассчитать установившуюся ошибку при изменении задающего воздействия по закону x = Vt, где скорость принять равной V = 10 с-1.Оценить величину ошибки в процентах от номинального значения регулируемой величины Ун= 3....................................................................................
7. Рассчитать статическую ошибку по возмущению F = Fн. Оценить ее величину в процентах от номинального значения регулируемой величины Ун = 3 (Fн =50В).............
Исходные данные. Структурная схема системы.
Задана исходная структурная схема системы автоматического регулирования (САР):
![]() F(p)
F(p)
 k6 .
k6 .
(T5p+1)р
![]()
 x(p) e(p) y1 y1-3 y2 y4
y5 y6
x(p) e(p) y1 y1-3 y2 y4
y5 y6
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() k1
k2 k4 k5
y(p)
k1
k2 k4 k5
y(p)
 y3 1 . T4p+1 (T5p+1)р
y3 1 . T4p+1 (T5p+1)р
![]()
![]() T3p+1
T3p+1
Puc. 1
Где y – регулируемая величина;
x – задающее воздействие;
e - ошибка регулирования;
y1, y2, y3, y4, y5, y6, y1-3 – промежуточные координаты;
k1, k2, k3, k4, k5 – передаточные коэффициенты звеньев;
T1, T2, T4 – постоянные времени.
Числовые значения параметров схемы приведены в таблице.
Таблица 1
|
k1 |
k2 |
k4 |
k5, с-1 |
k6 |
T3, мс |
T4, мс |
T5, мс |
|
28 |
50 |
14 |
0,5 |
0,04 |
0,05 |
0,05 |
0,05 |
Дополнительные данные V = 10 с-1, Ун = 3 В ,Fн =50 В.
1. Получение по структурной схеме системы уравнений динамики в оригиналах для динамических звеньев и сумматоров. Определение типа динамических звеньев.
1) Звенья и их типы
Звенья c W1(р) = k1 ,W2(р) = k2 , безинерционные . . . (пропорциональные) звенья.
Звенья W3(р) = 1/(Т3(р)+1) ,W4(р) = k4/(Т4(р)+1), инерционные (апериодические) звенья.
Звенья.
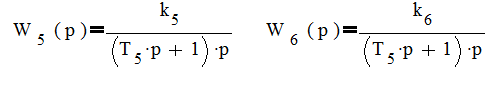 представляют собой
последовательное соединение интегрирующего и инерционного звеньев, т.е.
(инерционно- интегрирующее звено).Подробнее описаны
далее.
представляют собой
последовательное соединение интегрирующего и инерционного звеньев, т.е.
(инерционно- интегрирующее звено).Подробнее описаны
далее.
2) Запишем уравнения динамики для сумматоров:
X(p) – Y(p) = E(p) (1.1);
Y1(p) - Y3(p) = Y1-3(p) (1.2);
Y5(p) - Y6(p) = Y(p) (1.3);
3) Уравнения динамики для звеньев
E(p)×k1 = Y1(p) (1.4);
Y1-3(p)× k2= Y2(p) (1.5);
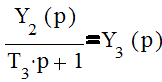 (1.6);
(1.6); 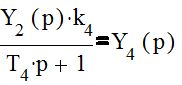 (1.7);
(1.7);
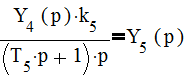 (1.8);
(1.8);
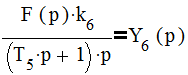 (1.9);
(1.9);
![]() Имеем систему уравнений .
Имеем систему уравнений .
![]() X(p)
– Y(p) = E(p) (1.1);
X(p)
– Y(p) = E(p) (1.1);
Y1(p) - Y3(p) = Y1-3(p) (1.2);
Y1(p) - Y3(p) = Y1-3(p) (1.3);
![]() E(p)×k1 = Y1(p) (1.4);
E(p)×k1 = Y1(p) (1.4);
![]()
![]() Y1-3(p)× k2=
Y2(p) (1.5);
Y1-3(p)× k2=
Y2(p) (1.5);
Y2(p)=Y3(p)×(T3×p+1) (1.10);
Y2(p)×k4 =Y4(p)×(T4×p+1) (1.11);
Y4(p)×k5 =Y5(p)×(T5×p+1)×p (1.12);
![]() F(p)×k6 =Y6(p)×(T5×p+1)×p
(1.13);
F(p)×k6 =Y6(p)×(T5×p+1)×p
(1.13);
Литература.
1. Юревич Е.И. Теория автоматического управления. Учебник для студентов высш. техн. учебн. Заведений. Изд. 2-е, перераб. и доп. Л., “Энергия”, 1975.
2. Методические указания к курсовой работе по дисциплине “Теория автоматического управления” для студентов специальности 21.05 всех форм обучения. /ГПИ, Горький, 1988.-31с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.