Нижегородский Государственный Технический Университет
по теории автоматического управления
гр.96 - ЭПА - 3
Проверил: Шахов А.В.
Принял: Шахов А.В.
-Нижний Новгород-
-1998-
1. Задание к работе и исходные данные.
2. Уравнения динамики в оригиналах для динамических звеньев и сумматоров
· система уравнений в изображениях по Лапласу
· система уравнений в оригиналах
3. Соединение второго и третьего звеньев:
· амплитудно-фазовая характеристика
· логарифмические частотные характеристики
· переходная характеристика
4. Передаточные функции
· системы разомкнутой по цепи главной обратной связи
· замкнутой системы для регулируемой величины и ошибки регулирования
5. Исследование устойчивости системы
· зависимость устойчивости от времени запаздывания( метод логарифмических частотных характеристик)
· качественный вид амплитудно-фазовых характеристик для областей устойчивости и неустойчивости
6. Расчет статической ошибки в системе при величине задающего воздействия х=1
· по уравнениям статики
· методом преобразований Лапласа (проверка)
1. Содержание задания.
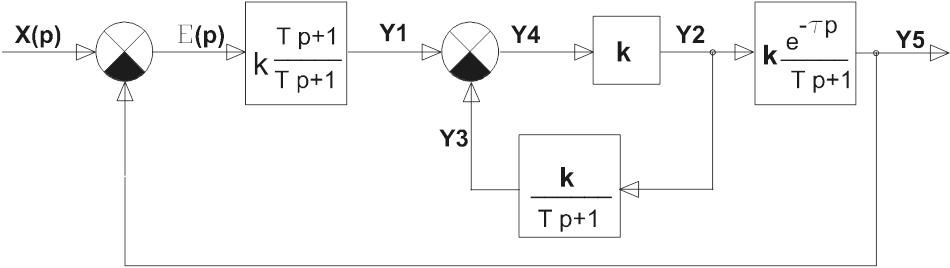
1.По структурной схеме (рис.1) получить систему уравнений динамики в оригиналах для динамических звеньев и сумматоров.
2.Расчитать и построить амплитудно-фазовую характеристику, л.а.ч.х., л.ф.ч.х. и переходную характеристику соединения второго и третьего звеньев.
3.По структурной схеме системы получить передаточную функцию системы, разомкнутой по цепи главной обратной связи, а так же передаточные функции замкнутой системы для регулируемой величины Y и ошибки Е по задающему воздействию X.
4.Исследовать методом логарифмических частотных характеристик разомкнутой системы влияние времени запаздывания t на устойчивость замкнутой системы. Показать качественный вид амплитудно-фазовых характеристик для каждой из полученных областей устойчивости и неустойчивости.
5.Расчитать статическую ошибку в системе при величине задающего воздействия x=1.
 |
 |
 |
2. Уравнения динамики в оригиналах для динамических звеньев и сумматоров.
2.1.Система уравнений динамики для звеньев и сумматоров (в изображениях по Лапласу).
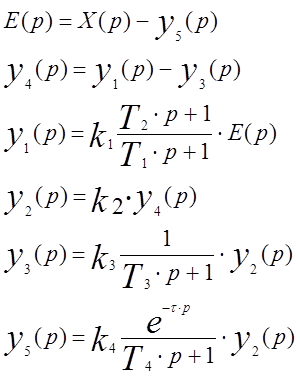 |
(первые два уравнения записаны для сумматоров, остальные – для звеньев 1,2,3,4 соответственно).
Исходя из полученных уравнений, можно сказать, что звено 1 – апериодическое с дифференцированием, звено 2 – усилительное, звено 3 – апериодическое, звено 4 – апериодическое с запаздыванием.
2.2.Система уравнений динамики для звеньев и сумматоров (в оригиналах).
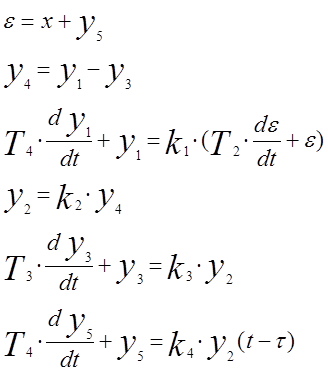 |
3.Соединение второго и третьего звеньев
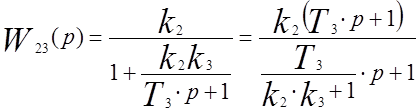 |
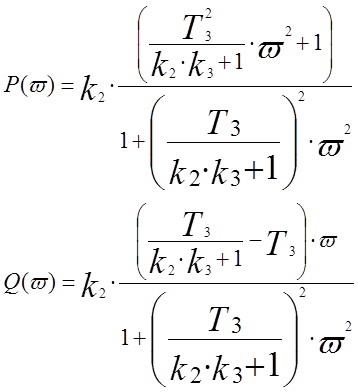 |
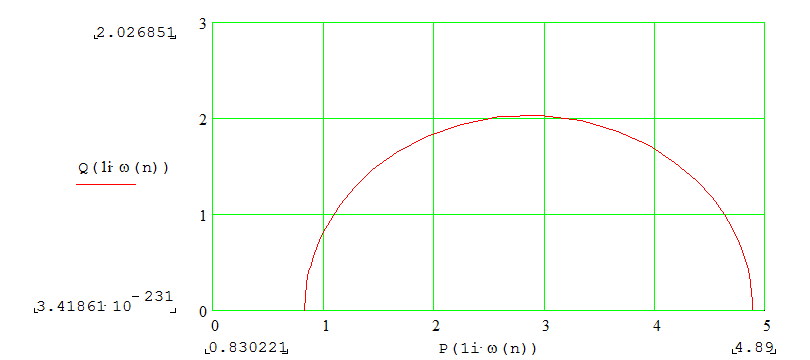 |
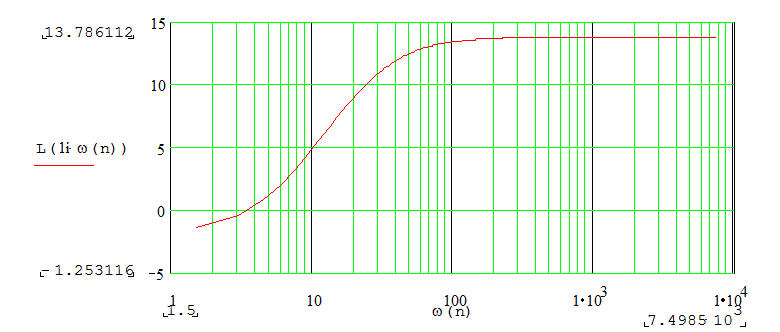
3.2 Логарифмические частотные характеристики
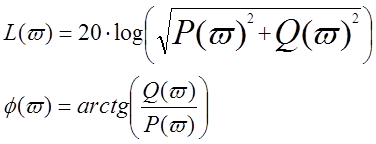 |
 |
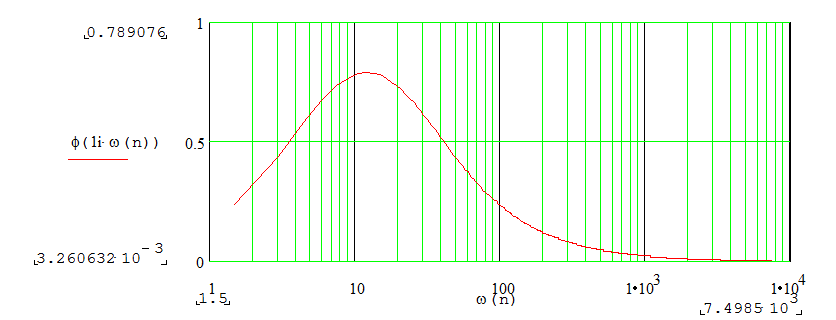 |
Рис.5
3.3 Переходная характеристика
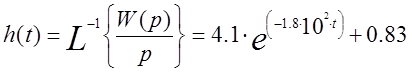 |
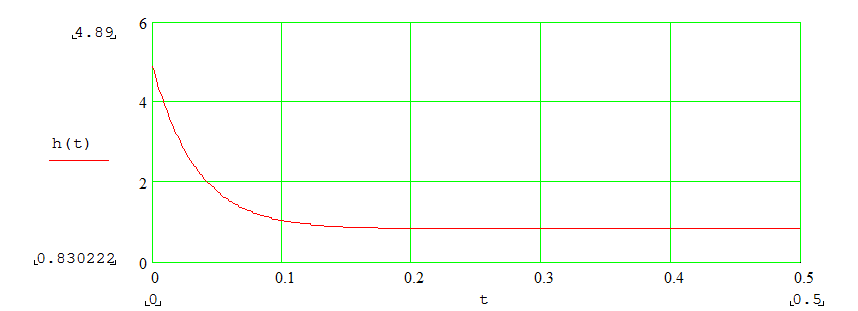 |
Рис.6
4.Передаточные функции
4.1.Передаточная функция системы, разомкнутой по цепи главной обратной связи получается при размыкании связи между выходом и входом системы (см. рис.7).
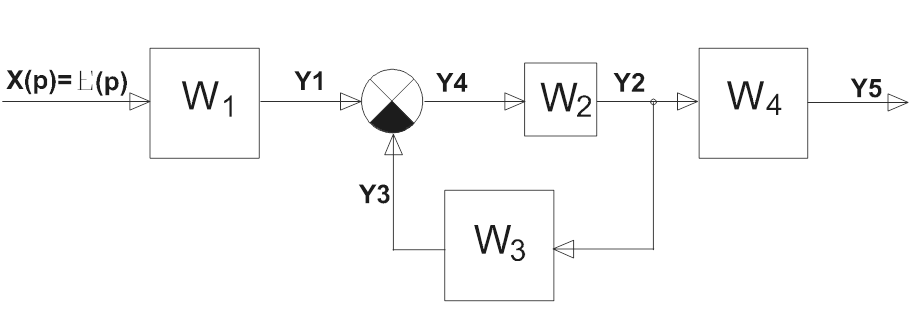 |
Рис.7
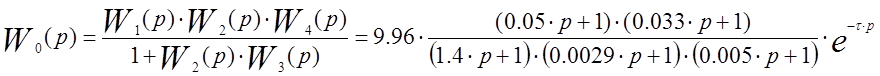 |
4.2.Передаточные функции замкнутой системы для регулируемой величины и ошибки регулирования по задающему воздействию получаем по структурной схеме системы, изображенной на рисунке 1:
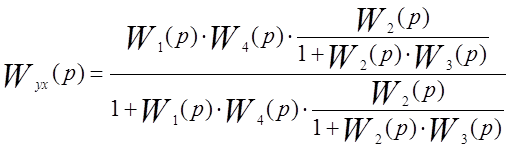 |
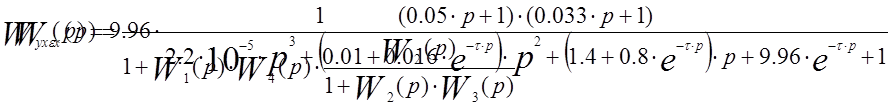 |
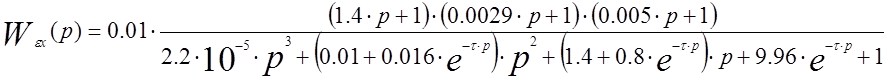 |
5.Исследование устойчивости системы
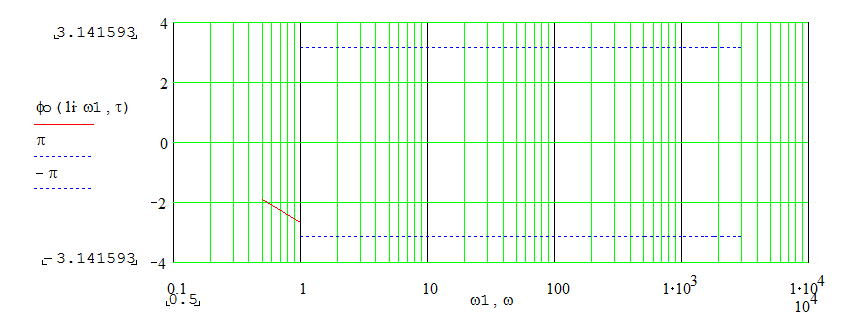
5.1.Зависимость устойчивости замкнутой системы от времени запаздывания исследуем с помощью логарифмических характеристик разомкнутой системы в следующем порядке:
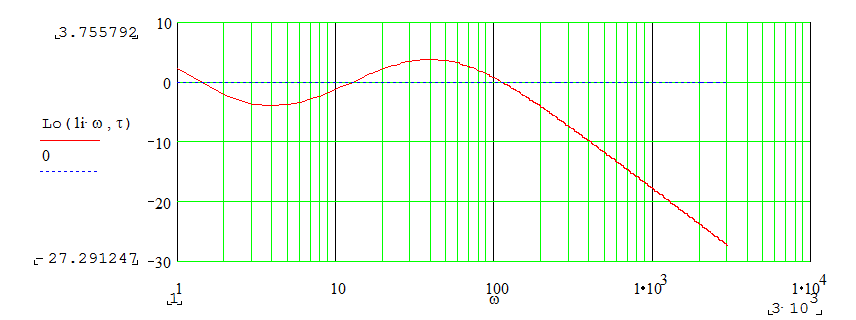 |
Рис.8
 |
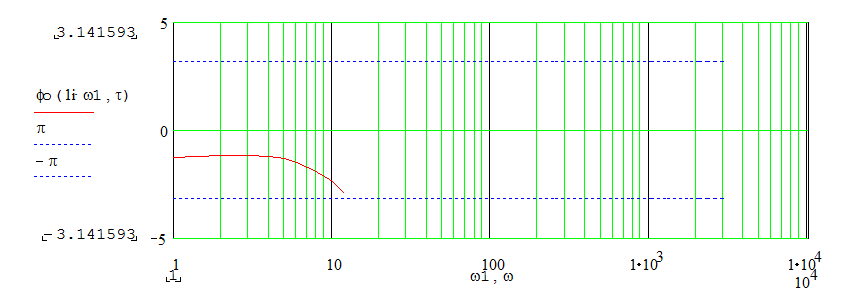 |
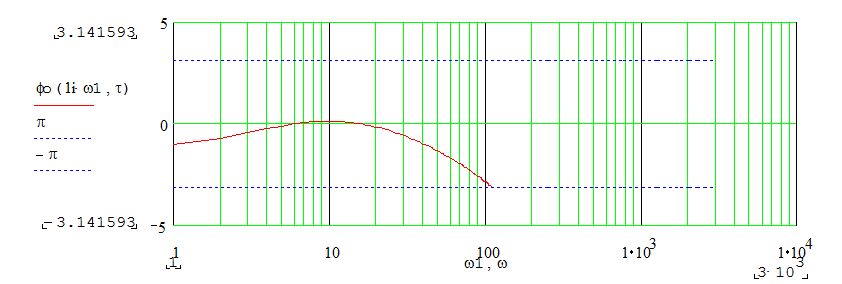 |
Т.о. получаем несколько областей изменения для времени запаздывания:
5.2.Характер поведения системы в каждой из полученных областей (устойчивость или неустойчивость) определяем по виду а.ф.х. в этой области (см.рис.12-15):
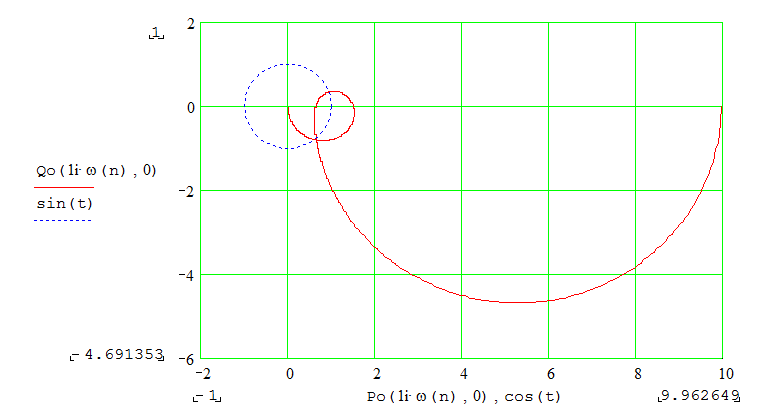 |
Рис.12
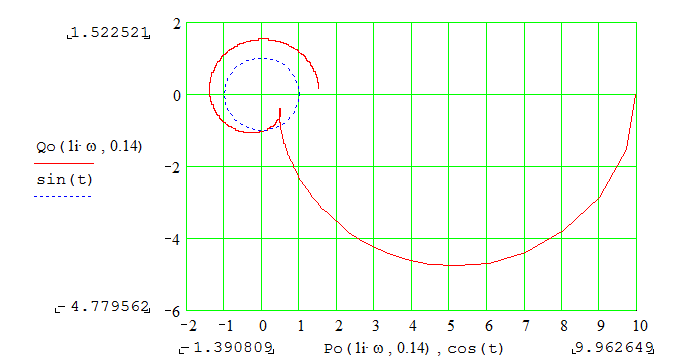 |
Рис.13
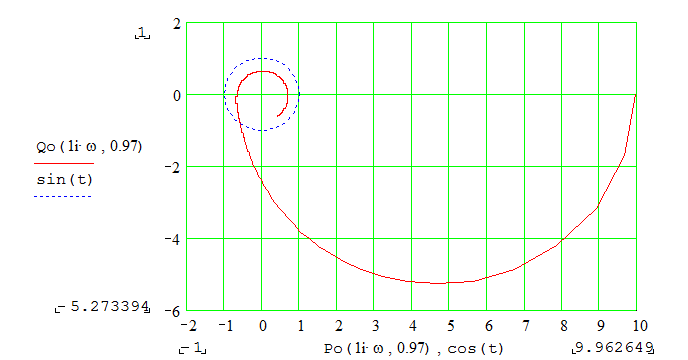 |
Рис.14
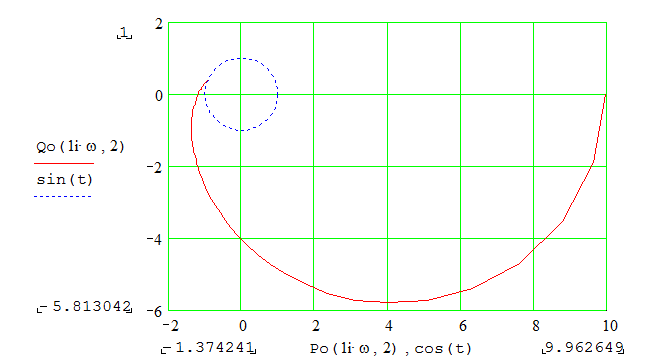 |
Рис.15
Анализируя приведенные графики, можно сделать вывод:
а) система устойчива при <0.02 и при 0.272< <1.678
б) система неустойчива при 0.02< <0.272 и при >1.678
6.Расчет статической ошибки в системе
6.1.Расчет установившегося режима по уравнениям статики.
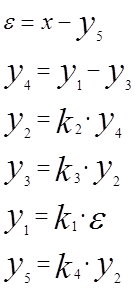 |
(как видно из полученных уравнений все звенья - статические)
Решаем полученную систему графически: составляем структурную схему статической системы (рис.8), находим передаточную функцию для ошибки по входному воздействию и, подставляя заданное значение х=1, находим статическую ошибку:
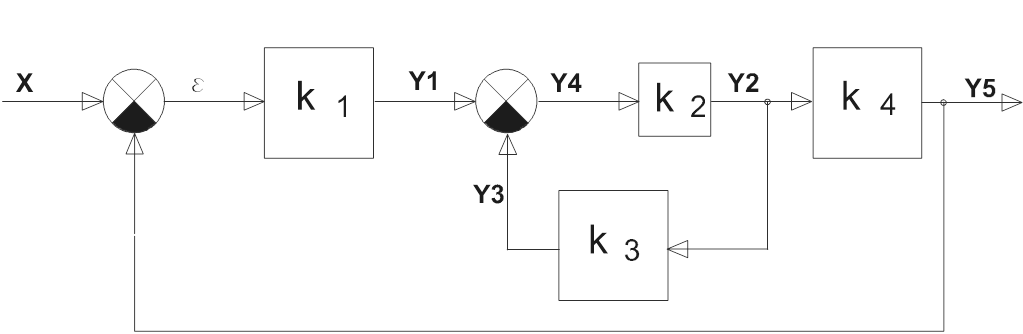
Рис.8
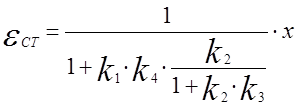 |
|||
6.2.Расчет по методу преобразований Лапласа (проверка).
Зная переходную функцию системы для ошибки по задающему воздействию (см. пункт 4.2.), величину задающего воздействия (х=1) и применяя теорему об установившемся значении оригинала, можно записать:
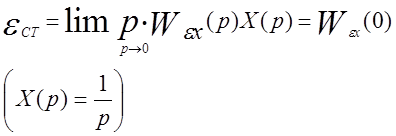 |
|||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.