Министерство образования Российской Федерации
Саратовский государственный технический университет
Балаковский институт техники технологии и управления
Факультет: вечерне-заочный
Кафедра: ВМиМ
Специальность: УИТ
Расчетно-графическая работа по электротехнике №1
по теме:
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ
Выполнила
студент гр. УИТ-2в
Проверил
Зайцев А.В.
Балаково 2008
1.
Дано:
Е=100В
L=5мГн
С=50мкФ
R1=2Ом
R2=8Ом
R3=6Ом
Найти iR.
Классический метод расчёта
1) Определяем ток через индуктивность в цепи до коммутации
![]()
![]()
2) Определяем
принужденное значение ![]() в цепи после коммутации
после окончания переходного процесса и составляем схему замещения
в цепи после коммутации
после окончания переходного процесса и составляем схему замещения
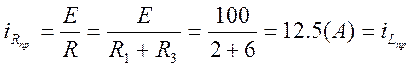
![]()
3) определяем свободный ток через индуктивность и свободно напряжение на емкости
![]()
![]()
4) Составляем характеристическое уравнение
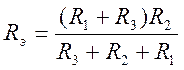
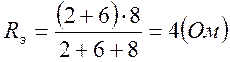
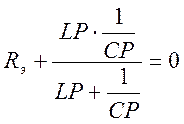
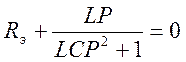
![]() - характеристическое уравнение.
- характеристическое уравнение.
![]()
![]()
![]()
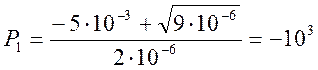
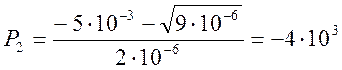
5) В зависимости от корней характеристического уравнения, записываем решение для свободной составляющей
![]()
6) Для расчета коэффициентов А1 и А2 составляем систему уравнений, состоящую из решения для свободной составляющей и производной от этого решения
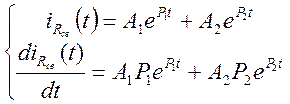
Эту систему переписываем для момента времени t=0
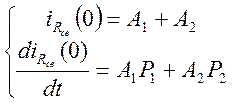
7) Используя
данные п.3, производим расчет коэффициентов A1
и А2. Составляем систему уравнений по первому и второму законам
Кирхгофа коммутационной схемы для мгновенных значений и берем первую
производную от этих уравнений, эту систему дополним уравнением 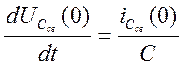 .
.
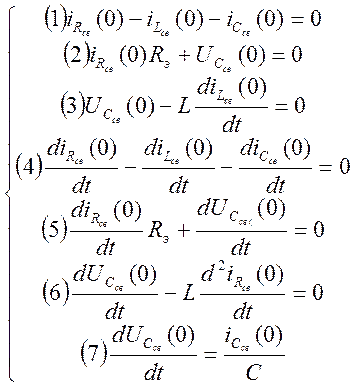
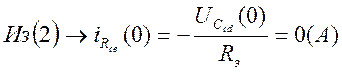
![]()
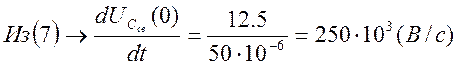
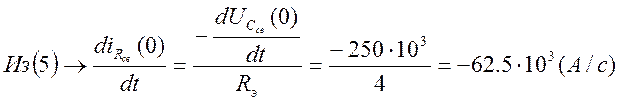
Т.о. ![]()
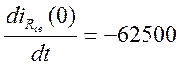
8) Решаем систему уравнений (п.6) и определяем коэффициенты А1 и А2
![]() А1+А2=0
А1+А2=0
![]()
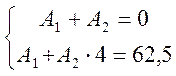
![]()
![]()
![]()
9)
Записываем решение для ![]() fсв(t) в соответствии с п.5
fсв(t) в соответствии с п.5
![]()
10)
Записываем общее решение для ![]()
![]()
11) Построим график iR(t)
|
|
|||||||
|
t |
0 |
0,0005 |
0,001 |
0,0015 |
0,002 |
0,0025 |
0,003 |
|
i |
20,8 |
2,81 |
0,38 |
0,04 |
0,006 |
0,001 |
0,0001 |
|
|
|||||||
|
t |
0 |
0,0005 |
0,001 |
0,0015 |
0,002 |
0,0025 |
0,003 |
|
i |
-20,8 |
-12,69 |
-7,7 |
-4,58 |
-2,9 |
-1,66 |
-1,04 |
|
|
|||||||
|
t |
0 |
0,0005 |
0,001 |
0,0015 |
0,002 |
0,0025 |
0,003 |
|
i |
12,5 |
2,62 |
5,18 |
7,96 |
9,61 |
10,84 |
11,46 |
Операторный метод расчета.
Операторная схема замещения
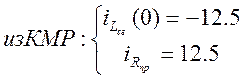
По методу узловых потенциалов
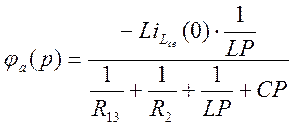
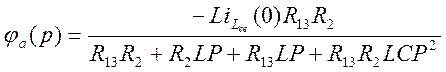
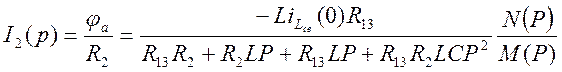
![]()
![]()
![]()
![]()
![]()
![]()
![]()
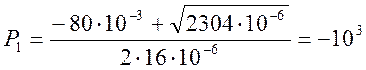
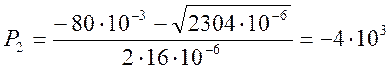
![]()
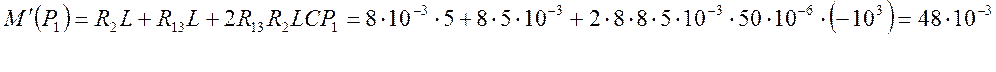
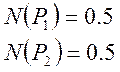
![]()
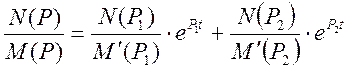
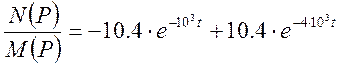
2. Найти i1.
На вход схемы
подается испытательная функция Хевисайда 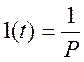 .
.
Операторная схема замещения изображается при нулевых начальных условиях
Z=R+LP
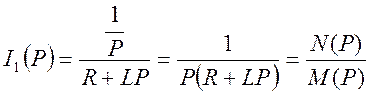
Переходим от изображения к оригиналу. Для этого решаем уравнение М(Р)=0
![]()
![]()
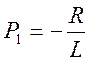
Переход от изображения к оригиналу при двух корнях:
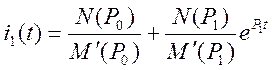
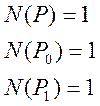
![]()
![]()
![]()
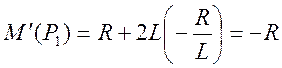
Подставим найденные величины в формулу для тока i1(t)
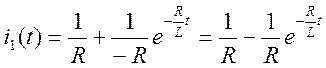
В связи с тем, что на вход схемы подавалась функция Хевисайда, переходная функция по току g(t) численно равна i1(t).
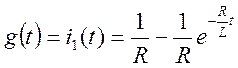
Записываем первый интеграл Дюамеля, работающий в пределе от 0 до t1.
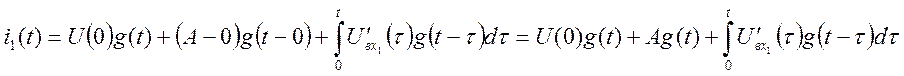
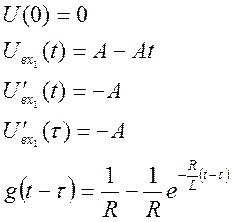
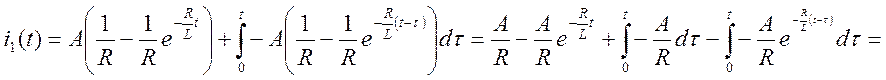
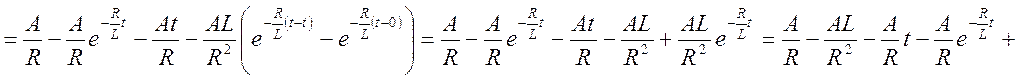
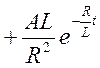 .
.
Записываем
второй интеграл Дюамеля, работающий в пределе от t1
до ![]() .
.
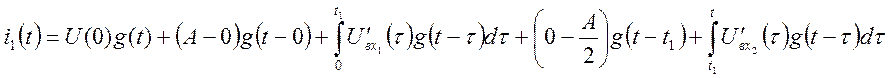
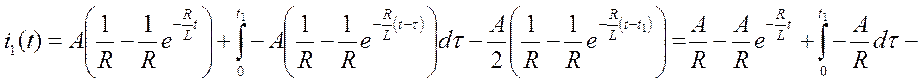
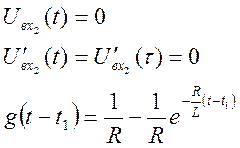
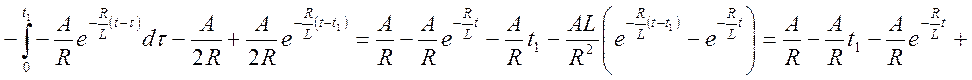
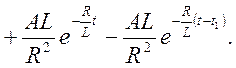
В итоге, первый интеграл Дюамеля имеет вид:
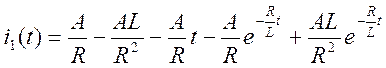 ,
,
Второй интеграл Дюамеля имеет вид:
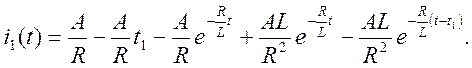
3. ![]()
![]()
![]()
Решение.
Находим изображение данной функции по Лапласу
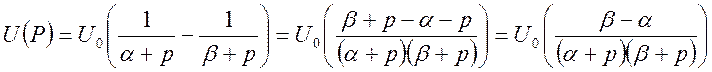
Находим спектр функции
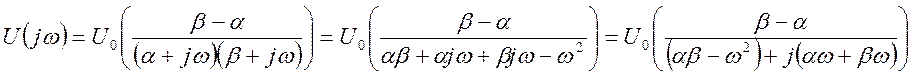
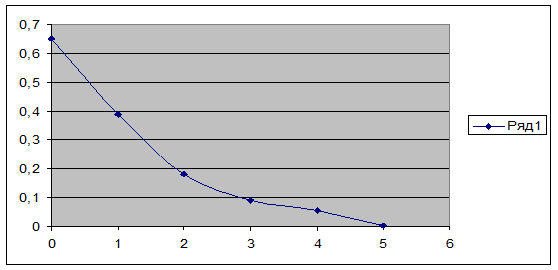
Находим модуль спектра
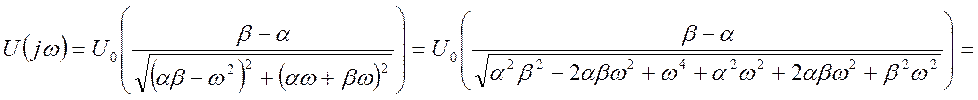
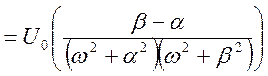
Переходим к относительным единицам
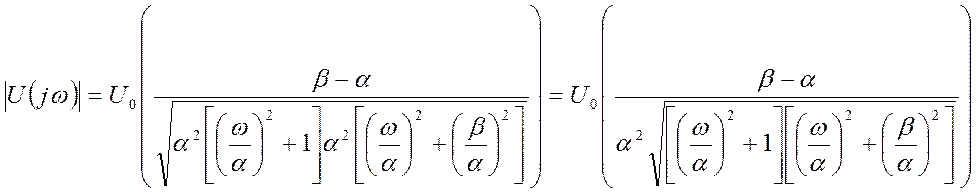
Обе части
уравнения разделим на 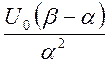
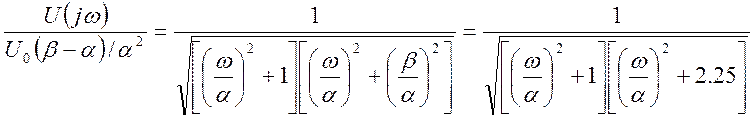
|
|
|
|
0 |
0,65 |
|
1 |
0,39 |
|
2 |
0,18 |
|
3 |
0,09 |
|
4 |
0,056 |
|
5 |
0,0037 |
Министерство образования Российской Федерации
Саратовский государственный технический университет
Балаковский институт техники технологии и управления
Факультет: вечерне-заочный
Кафедра: ВМиМ
Специальность: УИТ
Расчетно-графическая работа по электротехнике №2
по теме:
Цифровые и магнитные цепи
Выполнила
студент гр. УИТ-2в
Сафонова Маргарита
Проверил
Зайцев А.В.
Балаково 2008
1. ![]()
![]()
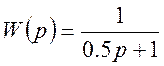
Решение:
Находим z-преобразование входной последовательности, используя табличные соотношения между дискретными функциями и их z-преобразованиями
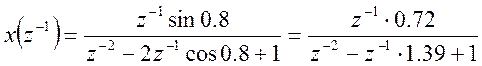
Переходим от передаточной функции аналогичного четырехполюсника W(р) к соответствующей передаточной функции цифрового W(z-1), используя обратную разность
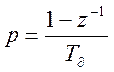
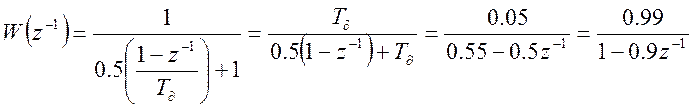
Реализуем передаточную функцию цифрового четырехполюсника в виде цифровой схемы
Находим z-преобразования выходной последовательности
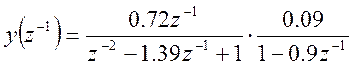
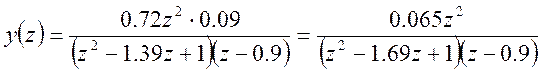
Находим выходную последовательность
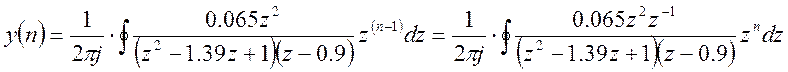
Обозначим
через 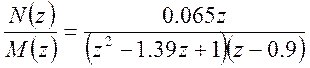
Решаем уравнение М(z)=0
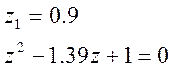
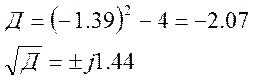
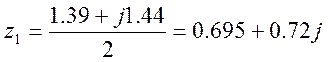
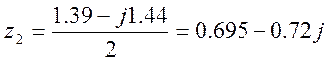
Переход к выходной последовательности при двух корнях идет в виде
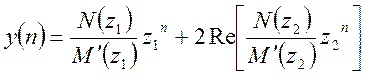
![]()
![]()
![]()
![]()
![]()
![]()
![]()
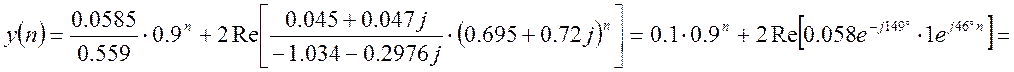
![]() .
.
2. Дано:
L1=45см,
S1=15,4см2,
W1=300,
I1=1А,
L2=22см,
S2=10,4см2,
L3=40см,
S3=15см2,
W3=400,
I3=0,5А,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.