Электротехника \ Электроника

Основы теории четырехполюсников, страница 4

3)   Частота, являющаяся границей между полосой пропускания и полосой задержания, называется граничной частотой или частотой среза (fгр. или fср.).

У реальных фильтров нет четкой границы между ПП и ПЗ, поэтому в них за значение граничной частоты fгр. принимают частоту определяемую из соотношения 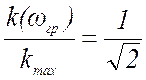 ≈ 0.707 ≈ 0.7.

4)  Скорость спада АЧХ коэффициента передачи Ku в полосе заграждения. Она рассчитывается из выражения

 V= - 20lg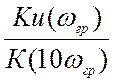Þ[]

Избирательные свойства фильтра тем лучше, чем ближе форма АЧХ к прямоугольной. Идеальный фильтр имеет прямоугольную АЧХ. Его скорость спада бесконечна.

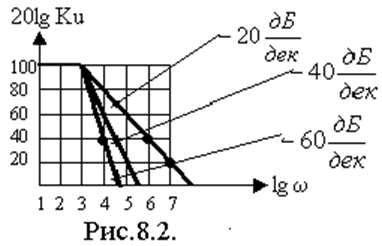
На рис.8.2. изображены амплитудно-частотные характеристики фильтра низких частот (ФНЧ) в логарифмическом масштабе при разных скоростях спада.

8.3. Классификация фильтров электрических сигналов

1)  в зависимости от характера входного сигнала фильтры делятся на аналоговые и цифровые.

2) в зависимости от наличия в схеме активных элементов: пассивные, активные.

3) в зависимости от элементов составляющих фильтр: LC , RC , RL - типа, АRC - типа (активные RC фильтры).

4) по характеру математического выражения аппроксимирующего АЧХ фильтра: фильтры Бесселя, фильтры Баттерворта, фильтры Золотарева, фильтры Чебышева и др.

5) по расположению полосы пропускания (ПП) на оси частот, фильтры делятся:

1. Фильтры низких частот  (ФНЧ). Их АЧХ коэффициента передачи приведена на рис. 8.3а. АЧХ идеального фильтра имеет прямоугольный характер, а у реального нет четкой границы между полосой пропускания и полосой заграждения.

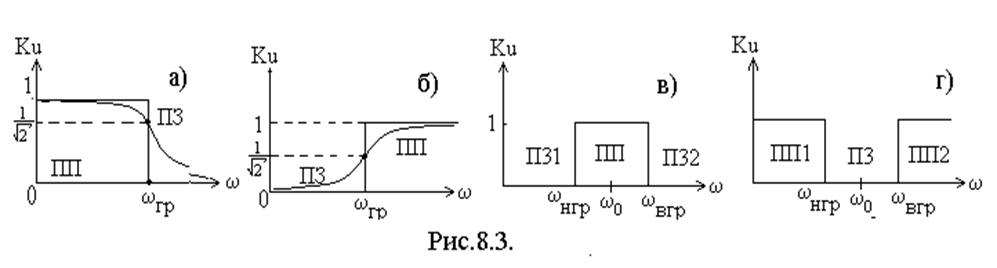2 Фильтры высоких частот (ФВЧ). Их АЧХ коэффициента передачи приведена на рис. 8.3б.

3. Полосно – пропускающие фильтры (ППФ). ). Их АЧХ коэффициента передачи приведена на рис. 8.3в, где ω 0  - средняя частота полосы пропускания; ωв гр, ωн гр – соответственно, верхняя и нижняя граничные частоты полосы пропускания. Если ω0/(ωв гр- ωн гр) >>1, то фильтры называют избирательными, такие фильтры пропускают сигналы в узком диапазоне частот.

4.  Полосно – заграждающие фильтры (ПЗФ). Их АЧХ коэффициента передачи приведена на рис. 8.3в, где ω 0  - средняя частота полосы задержания; ωв.гр, ωн.гр – соответственно, верхняя и нижняя граничные частоты полосы задержания. Если ω0/(ωв.гр- ωн.гр) >>1,то фильтры называют режекторными, они подавляет сигнал в узком диапазоне частот.


8.4. Схемы электрических фильтров

Основой для построения фильтров является каскадное (последовательное) соединение Г-, Т- или П-образных четырехполюсников. Каждый из четырехполюсников, в теории фильтров, называют звеном фильтра.


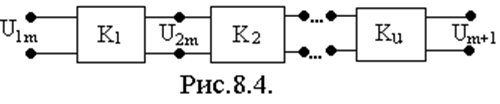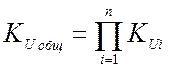Если звенья фильтров удовлетворяют условию Rвых<<Rвх то такие звенья можно считать независимыми так как они не влияют на коэффициент передачи по напряжению друг друга. В этом случае общий коэффициент передачи фильтра КUобщ можно записать как произведение коэффициентов передач КUi отдельных звеньев, входящих в фильтр

.

8.4.1. Схемы звеньев фильтра

Избирательные свойства звеньев фильтра и фильтра в целом объясняются тем, что в их схему входят элементы (катушки индуктивности и емкости) сопротивления которых зависят от частоты.

15.1.1.1  Для простейшей Г-образной схемы с комплексными сопротивлениями Z1 и Z2, коэффициент передачи по напряжению определяется выражением

15.1.1.2  .

Отсюда следует, что на частотах когда |Z2|>>|Z1|, то Кu→1 это полоса пропускания. На тех частотах, когда |Z2|<<|Z1|, то Кu→0, это полоса заграждения.

Рассмотрим конкретные схемы звеньв фильтра.

1) Простейшие схемы однозвенных ФНЧ приведены на рис.8.5.

На рис.8.5 а, б и в приведены Г-образные схемы, соответственно, RC-типа,


 RL-типа и LC-типа типа, а на рис.8.5 г, д приведены схемы Т- и П-образные схемы на LC-элементах. Работа, например, фильтра RC-типа, происходит следующим образом. Если ω→0, то сопротивление конденсатора (1/ωС)→∞, а следовательно U2m = U1m , т.е. сигнал передается через цепь без ослабления. При увеличении частоты входного сигнала сопротивление конденсатора уменьшается, (1/ωС)→0. Амплитуда выходного напряжения на конденсаторе |U2m|→0 и, следовательно, высокочастотный сигнал через фильтр не проходит, т.е. подавляется.

Комплексный коэффициент передачи по напряжению Ku(jw)=U2m/U1m, и амплитудно-частотная характеристика (АЧХ) -  Ku(w)=U2m/U1m , рассмотренного ФНЧ определяются из выражений

Кu(jω)=(1+jω RC)-2,               Кu(ω)=(1+(ωRC)2)-2.

2) Простейшие схемы однозвенных ФВЧ приведены на рис.8.6.

На рис.8.6 а, б и в приведены Г-образные схемы, соответственно: RC-типа, RL-типа и LC-типа, а на рис.8.5 г, д приведены схемы Т- и П-образные схемы на LC-элементах. Работа, например, фильтра RC-типа, происходит следующим образом. Если ω→0, то сопротивление конденсатора (1/ωС)→∞, а следовательно U2m→0, т.е. низкочастотный сигнал через фильтр не проходит, т.е. подавляется. При увеличении частоты входного сигнала сопротивление конденсатора уменьшается (1/ωС)→0, следовательно, U2m = U1m , т.е. высокочастотный сигнал передается через цепь без ослабления.


3) Полосно-пропускающий фильтр (ППФ) можно получить путем последовательного соединения двух звеньев ФНЧ и ФВЧ, подобрав соответствующим образом их граничные частоты.


Однако на практике, часто, используют схему моста Вина (рис.8.7а). На рис. 8.7б приведена зависимость его коэффициента передачи от частоты. На рис.8.7в приведена схема ППФ на основе последовательного контура.

4) Полосно-заграждающий фильтр (ПЗФ) можно получить путем последовательного соединения ФНЧ и ФВЧ при соответствующем выборе граничных частот.

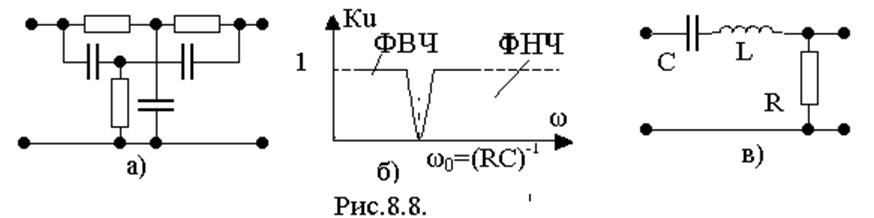
Однако на практике, часто, используют схему двойного Т-образного моста (рис.8.7а). Зависимость коэффициента передачи от частоты этой схемы приведена на рис. 8.7б. Аналогичной характеристикой обладает схема на основе последовательного контура (рис.8.7в).


8.4.2. Влияние числа звеньев фильтра на его характеристики

Скачать файл