ГЛАВА 7
Основы теории четырехполюсников
7.1. Основные определения. Уравнения и параметры четырехполюсника
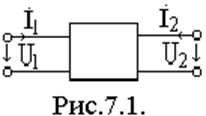
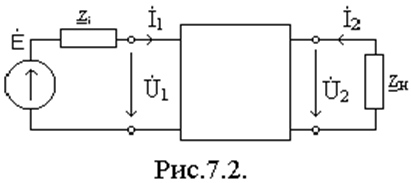
Теория четырехполюсников – это один из способов описания электрической цепи, когда схема электрической цепи может быть не известна. В теории четырехполюсников электрическую цепь заменяют «черным ящиком» с четырьмя выводами, два из которых являются входными (1, 11), а два других – выходными (2, 21).
 Режим работы цепи и все ее
параметры известны (можно рассчитать), если известны входные и выходные токи и
напряжения. При этом:
Режим работы цепи и все ее
параметры известны (можно рассчитать), если известны входные и выходные токи и
напряжения. При этом:
U1, I1 – напряжение и ток на входе,
U2, I2 – напряжение и ток на выходе.
Однако это бывает излишнем, теория четырехполюсников позволяет описывать электрическую цепь, для которой известны две из этих четырех величин и параметры четырехполюсника определенные в режиме короткого замыкания и холостого хода на входе и выходе цепи. Две известные величины называют воздействием, обозначим их Х1, Х2 (это независимые переменные), а две другие откликом, обозначим их Y1, Y2 (это зависимые переменные, т. е. функции).
Уравнения, устанавливающие связь между откликами и воздействиями называют основными уравнениями четырёхполюсника. В общем виде, их можно записать, как две некоторые функции f1 и f2 от (х1 и х2), однако для линейных цепей, в соответствии с принципом суперпозиции, эти функции обращаются в линейную комбинацию переменных (х1 и х2)
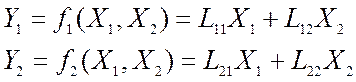
Коэффициенты L11, L12, L21, L22, входящие в основные уравнения четырехполюсника, называются параметрами четырехполюсника. В зависимости от того, что считать воздействием (аргументами) Х1, Х2 и что откликом (функциями) Y1, Y2 (см. табл.7.1), можно записать шесть пар основных уравнений четырехполюсника.
Таблица 7.1.
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
Воздействие |
|
|
|
|
|
|
|
Отклик |
|
|
|
|
|
|
|
Параметры |
|
|
|
|
|
|
7.2. Z – параметры четырехполюсника
Связь между напряжениями, токами и Z – параметрами получают из уравнений U1=f1(I1,I2), U2=f2(I1,I2). Если считать четырехполюсник линейным, то в силу принципа суперпозиции, функции представляют собой линейную комбинацию аргументов т. е.
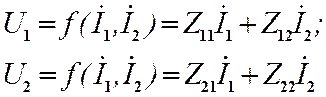
Коэффициенты, входящие в эти уравнения имеют размерность сопротивлений и называются Z – параметрами, а сами уравнения - уравнениями четырехполюсника с Z – параметрами. Эти параметры имеют следующие названия:
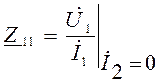 - входное сопротивление при режиме
холостого хода (Х.Х) на выходе;
- входное сопротивление при режиме
холостого хода (Х.Х) на выходе;
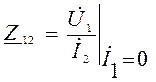 -сопротивление
обратной передачи при Х.Х. на входе;
-сопротивление
обратной передачи при Х.Х. на входе;
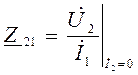 -
сопротивление прямой передачи при Х.Х. на выходе;
-
сопротивление прямой передачи при Х.Х. на выходе;
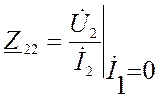 - выходное сопротивление при Х.Х. на
входе.
- выходное сопротивление при Х.Х. на
входе.
В общем случае, приналичие в схеме реактивных элементов эти сопротивления являются комплексными.
Полученную систему уравнений можно записать в матричной форме
(U)=(Z) (I),
где (I)=(I1,I2)т – матрица-столбец заданных токов, (U)=(U1,U2)т – матрица-столбец напряжений на выводах четырехполюсника,
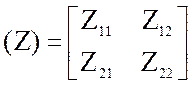 - матрица сопротивлений
четырехполюсника.
- матрица сопротивлений
четырехполюсника.
Аналогично можно записать и остальные уравнения четырехполюсника.
Например: Y-параметры. Основные уравнения четырехполюсника в y-параметрах записываются как
![]() ,
,
а Y-параметры имеют следующие названия:
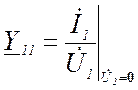 -
входная проводимость в режиме короткого замыкания на выходе;
-
входная проводимость в режиме короткого замыкания на выходе;
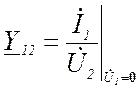 -
проводимость обратной передачи в режиме короткого замыкания на входе;
-
проводимость обратной передачи в режиме короткого замыкания на входе;
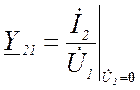 -
проводимость прямой передачи при коротком замыкании на выходе;
-
проводимость прямой передачи при коротком замыкании на выходе;
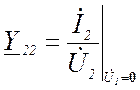 -
выходная проводимость в режиме короткого замыкания на входе.
-
выходная проводимость в режиме короткого замыкания на входе.
Причем 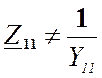 , т.к. они определены при разных
режимах.
, т.к. они определены при разных
режимах.
Параметры различных систем уравнений относящиеся к одному четырехполюснику взаимосвязаны, т.е. любой из параметры одной системы уравнений (например z-параметры) могут быть выражены через параметры другой системы (например у, h, g и т.д.). Кроме того, все параметры четырехполюсника связаны с функциями цепи.
7.3. Связь между функциями цепи и параметрами
четырёхполюсника
К основным параметрам (функциям) электрической цепи относят ![]() . Покажем, что все они могут быть
выражены через Z - параметры четырёхполюсника:
. Покажем, что все они могут быть
выражены через Z - параметры четырёхполюсника: ![]() .
Так как функции цепи и Z-параметры четырехполюсника характеризуют свойства
одного и того же четырёхполюсника, то все они связаны между собой. Установим
связь между функциями цепи и параметрами четырёхполюсника.
.
Так как функции цепи и Z-параметры четырехполюсника характеризуют свойства
одного и того же четырёхполюсника, то все они связаны между собой. Установим
связь между функциями цепи и параметрами четырёхполюсника.
 Запишем основные уравнения в Z – параметрах и
закон Ома для Zн и обозначим, записанные уравнения как (1), (2), (3).
Запишем основные уравнения в Z – параметрах и
закон Ома для Zн и обозначим, записанные уравнения как (1), (2), (3).
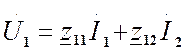 (1);
(1);
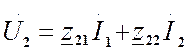 (2);
(2);
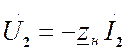 (3).
(3).
Подставим (3) ® (2). Получим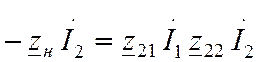 .
.
Разрешим это уравнение относительно I2.
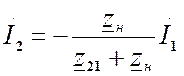 , обозначим
- (4).
, обозначим
- (4).
Подставим (4) ® (1), получим 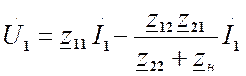 ,
обозначим - (5).
,
обозначим - (5).
Используя определения функций цепи, выразим их через Z-параметры.
1) Используя определение входного сопротивления и (5) получим
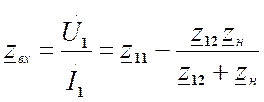 ;
если zн ®¥, то zвх
= z11.
;
если zн ®¥, то zвх
= z11.
2) Используя определение коэффициента передачи тока и (4) получим
 .
.
3) Используя определение коэффициента передачи
напряжения и (3) и (5) получим 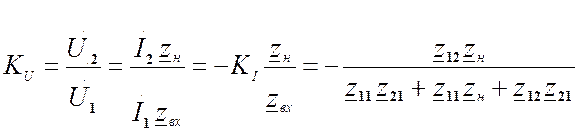 .
.
4) Используя определение выходного сопротивления получим
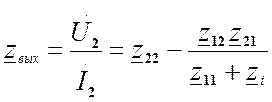 .
.
7.4. Эквивалентные схемы четырёхполюсника
Электрическая схема реального четырёхполюсника может быть сложной или даже недоступной, например, транзистор. Поэтому представляет интерес замена схемы реальной электрической цепи некоторой простой эквивалентной схемой.
Схемы называются эквивалентными, если при их взаимной замене входные и выходные токи и напряжения не изменяются. Эквивалентные схемы можно составлять разными способами:
1) по заданной топологии (по расположению элементов) электрической цепи;
3) по основным уравнениям четырехполюсника, такие схемы называют формальными схемами замещения.
3) по физической модели – это физическая схема замещения
7.4.1. Схемы замещения по заданной топологии
Обычно, в качестве эквивалентных схем выбирают схемы с минимальным числом элементов. Наиболее распространены Т-, П- и Г- образные схемы замещения (рис.7.3).
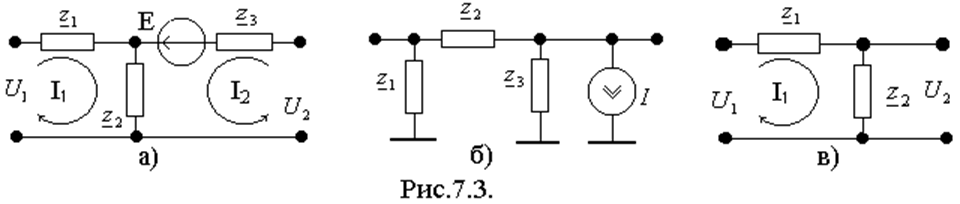 |
![]() ,
,
![]() .
.
Если цепь пассивна, то E = 0, то составленные уравнения совпадают с уравнениями z-параметров четырехполюсника, отсюда и определим z-параметры
![]() ;
; ![]() ;
;
![]() ; отсюда получим
; отсюда получим
![]() ;
; ![]() ,
,![]() .
.
Электрические цепи, не содержащие источников
электрической энергии, называются пассивными. Для пассивных
электрических цепей выполняется условие ![]() . Пассивные цепи для своего описания требуют трех
параметров, четвертый определяется из условия пассивности
. Пассивные цепи для своего описания требуют трех
параметров, четвертый определяется из условия пассивности ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.