ЦЕЛЬ РАБОТЫ: освоение математических методов теории систем, приобретение практических навыков анализа систем с применением современных программных и технических средств.
|
|
|

![]()
![]()
![]()
![]()
![]()
![]()
![]()




![]()
![]()
|

![]()
|
|
|
|
|
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
|
|
Рис. 1
|
№ варианта |
Параметры элементов эквивалентной схемы объекта управления. |
Выходная переменная |
|||||||||
|
R1, Ом |
R2, Ом |
R3, Ом |
R4,Ом |
R5, Ом |
L1, Гн |
L2, Гн |
L3, Гн |
С1,мкФ |
С2мкФ |
||
|
10 |
328 |
395 |
118 |
215 |
- |
24 |
24 |
- |
- |
19605 |
I1 |
1. Построение математической модели ОУ в пространстве состояния.
(Вычисления производятся в системе MathCad)
|
|
|
|
В третьем уравнении есть интеграл, поэтому дифференцируем его

Берем уравнение 4, в котором есть уравнение второго и первого порядка и в качестве фиктивной переменной Х1 выбираем элементы данного уравнения с производными на один порядок выше
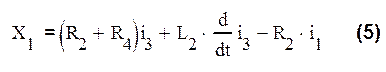
Вводим фиктивную переменную Х2, полученную из (4) с производными выше на 2 порядка:
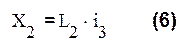
Из второго уравнения находим фиктивную переменную Х3:
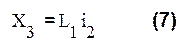
Производные от фиктивных переменных:
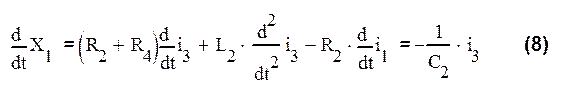 следует из (4)
следует из (4)
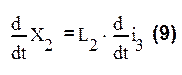
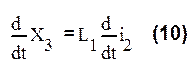
В данных уравнениях имеется 6 переменных i1, i2, i3, x1x2x3
Необходимо уйти от i1, i2, i3 выразив их через x1x2x3
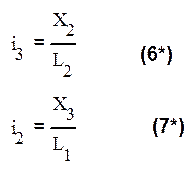
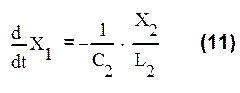 следует
из (8)
следует
из (8)
Подставим в (1) выражения для токов (6*), (7*):
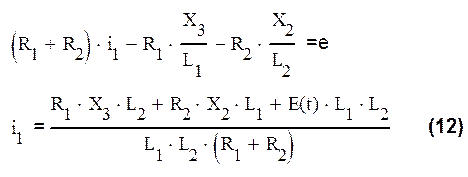 – выходная величина
– выходная величина
Из (5) находим ![]() и подставляем в (9):
и подставляем в (9):
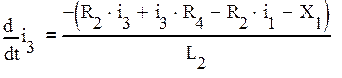
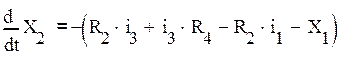
В полученном выражении заменим токи, используя выражения (6*) и (12):
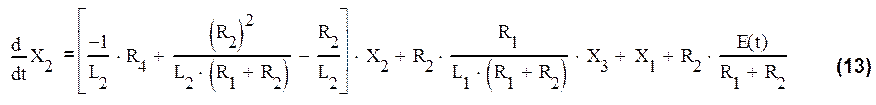
Из (2) находим ![]() и подставляем в (10):
и подставляем в (10):
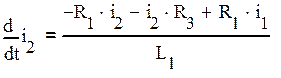
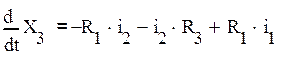
В полученном выражении заменим токи, используя выражения (7*) и (12):
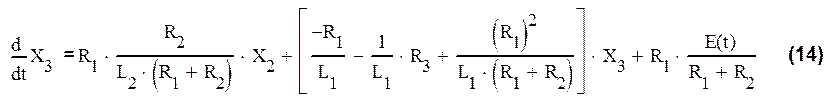
Теперь имеем выраженные выражения в зависимости от x1, x2, x3 и е(t).
Запишем математическую модель данной системы в нормальной форме Коши:
![]() - уравнение наблюдения U=|e| – ЭДС
- уравнение наблюдения U=|e| – ЭДС
![]() - уравнение выходной величины объекта.
- уравнение выходной величины объекта.
Основываясь на (11)-(14) получаем:
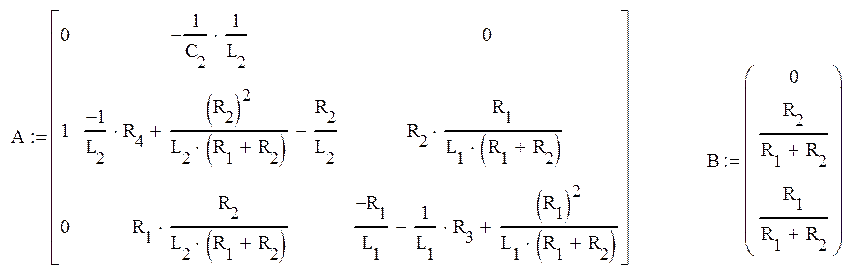
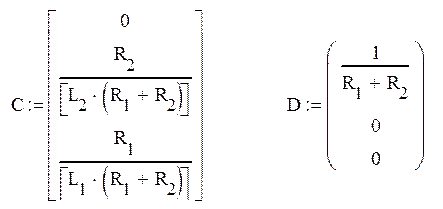
Подставим исходные данные (19605мкФ=0.019605Ф) и получаем математическую модель в пространстве состояний:
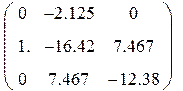
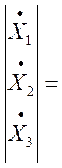
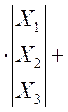
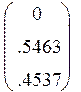
![]()
![]()
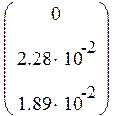
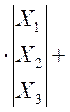
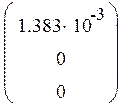
![]()
2. Построение структурной схемы и сигнального графа

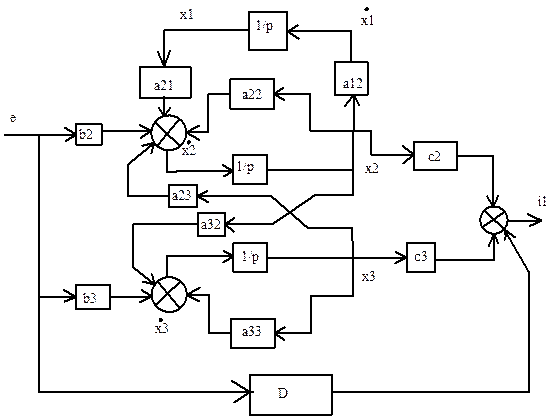
3.Построение передаточной функции схемы с использованием формулы Мейсона.
Для упрощения нахождение передаточной функции, упростим граф, используя основные принципы преобразования:
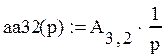
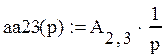
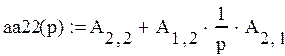 , тогда
получим граф :
, тогда
получим граф :

|
Прямые пути графа:
|
Замкнутые контуры:
|
|
|
|
|
|
Определитель графа: ![]()
Определители путей:
![]()
Передаточная функция графа и всей системы:
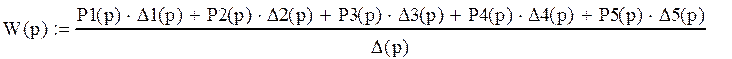
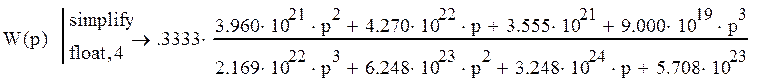
4. Определим временные и частотные характеристики и построим их графики.
Временные характеристики:
Переходная функция:
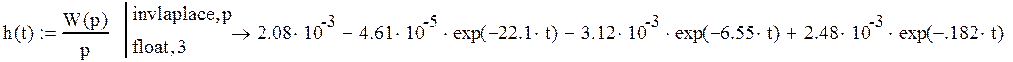
Импульсная функция:
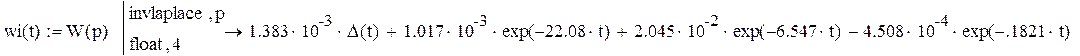
Частотные характеристики:
АЧХ:
![]()
ФЧХ:
![]()
Графики функций:
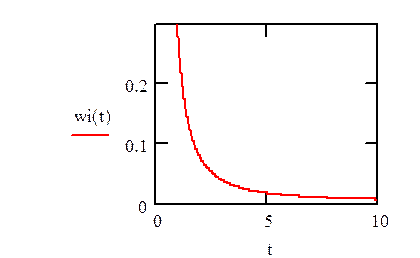
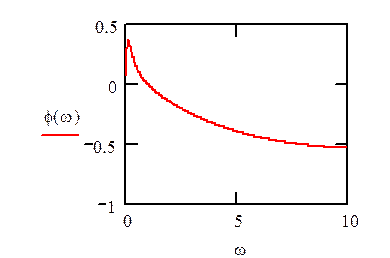
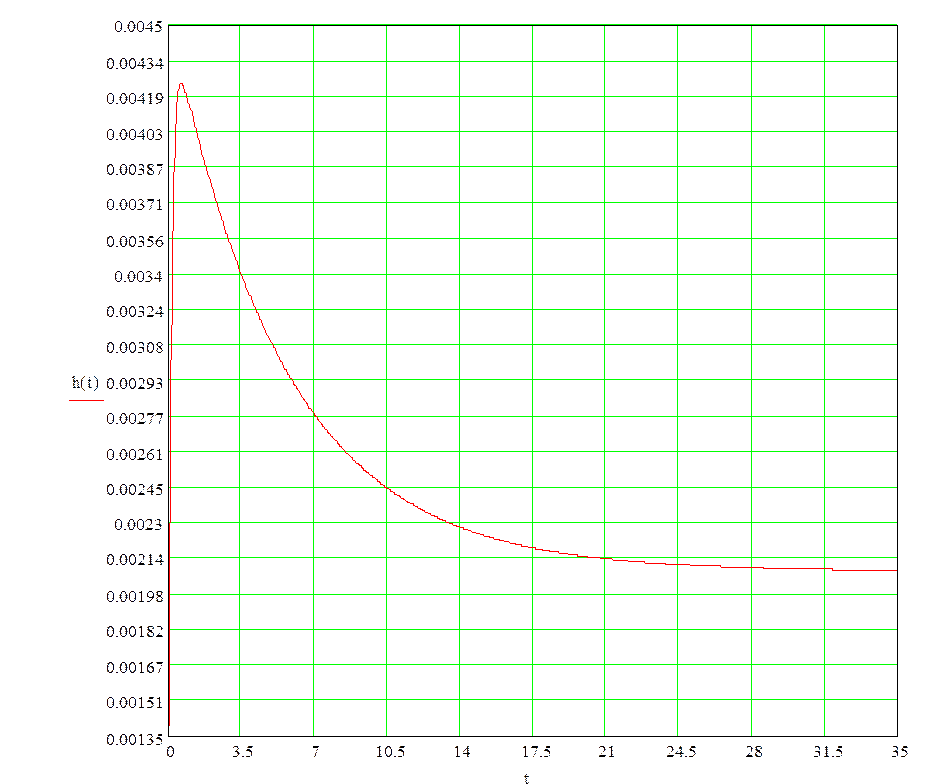
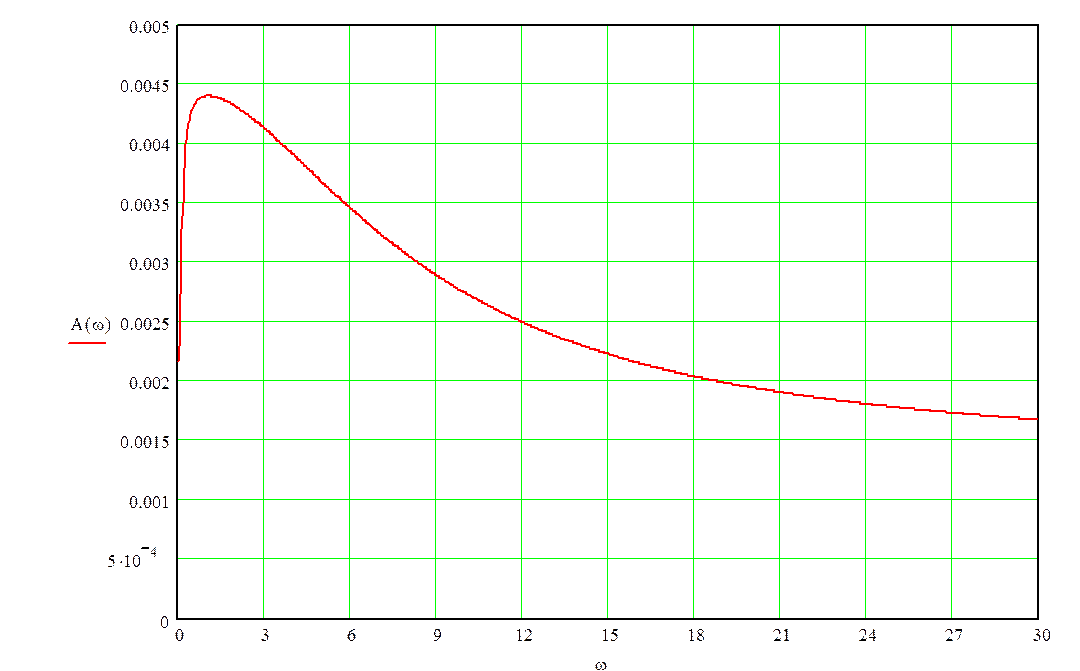
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.