Задание: Оптимизация расходометра переменного перепада давления
Данные: -1 +1
x1 - ширина цилиндрической части отверстия 0,005D 0,02D
x2 - площадь
отверстия (![]() ) 0,05
0,64
) 0,05
0,64
x3 - толщина
диска (![]() )
0,008D 0,05D
)
0,008D 0,05D
D=50мм
|
Факторы |
Уровни факторов |
|
|
-1 |
+1 |
|
|
x1 |
0,250 |
1 |
|
x2 |
0,05 |
0,64 |
|
x3 |
0,4 |
2,50 |
Проведем оптимизацию полнофакторного эксперимента,
Будем рассматривать задачу с максимальным числом факторов равным трем и числом опытов 23=8.
Составим матрицу планирования для линейной модели в первом приближении.
|
№ |
х0 |
х1 |
х2 |
х3 |
|
|
|
|
|
|
1 |
+ |
- |
- |
- |
38,46;38,63 |
38,545 |
0,014 |
38,591 |
0,00214 |
|
2 |
+ |
- |
+ |
- |
37,21;37,42 |
37,315 |
0,022 |
37,351 |
0,00131 |
|
3 |
+ |
+ |
- |
- |
36,38;36,49 |
36,435 |
0,00605 |
36,531 |
0,00926 |
|
4 |
+ |
+ |
+ |
- |
35,41;35,53 |
35,47 |
0,0072 |
35,291 |
0,032 |
|
5 |
+ |
- |
- |
+ |
34,64;34,86; 37 |
34,75 |
0,024 |
34,671 |
0,0062 |
|
6 |
+ |
- |
+ |
+ |
33,35;33,52 |
33,435 |
0,014 |
33,431 |
0,000014 |
|
7 |
+ |
+ |
- |
+ |
32,57;32,78 |
32,675 |
0,022 |
32,611 |
0,00406 |
|
8 |
+ |
+ |
+ |
+ |
31,13;31,32 |
31,225 |
0,018 |
31,371 |
0,021 |
Подсчитываем средние значения в сериях Y.
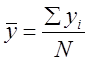 (1)
(1)
где уi – i-ое значение в серии опытов;
N – количество опытов в серии.
Подсчитываем дисперсию S2 различных серий опытов.
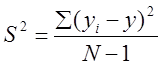 (2)
(2)
Проверяем пятую серию опытов на наличие ошибки.
Так как дисперсия S2=0,024, то
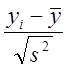 =14,524>t=12,71 (3)
=14,524>t=12,71 (3)
где t – коэффициент Стьюдента для степени свободы (n – 1)=(2 – 1)=1.
А значит, значение опыта равное 37 – промах и из дальнейшего рассмотрения мы его исключаем.
Проверяем дисперсию на однородность.
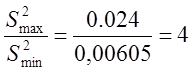 (4)
(4)
Полученное значение меньше табличного значения критерия Фишера равного F=164,4 для степеней свободы числителя f2=n–1=1 и знаменателя f1=n–1=1.
Находим дисперсию выходного параметра.
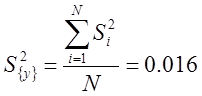 (5)
(5)
Записываем линейную модель в первом приближении в виде:
у=b0+b1х1+b2х2+ b3х3 (6)
пренебрегая влиянием составляющих второго порядка.
Вычисляем коэффициенты по формуле:
bi=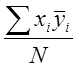 (7)
(7)
Получили следующие коэффициенты:
b0=34,981;
b1=-1,03; (8)
b2=-0,62;
b3=-1,96;
Линейная модель запишется в виде:
у=34,981-1,03х1 -0,62х2 -1,96х3 (9)
Рассчитываем по этой модели расчетные значения параметра оптимизации
у = f(x) и заносим эти значения в таблицу.
После чего находим квадрат отклонения расчетного значения от экспериментального
![]() (10)
(10)
и заносим полученные значения в таблицу.
Затем находим дисперсию адекватности для равномерного дублирования
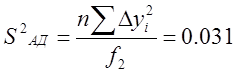 (11)
(11)
Где f2 = N – (n + 1) =5
Проверяем модель на адекватность, для чего находим расчетный коэффициент Фишера как отношение:
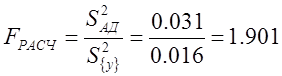 (12)
(12)
Полученное значение сравниваем с табличным значением критерия Фишера F = 6,6 для f1 = n –1 и f2 = 5 и поскольку полученное значение не превышает его, то полученная линейная модель адекватна.
Оценим значимость коэффициентов, для чего найдем дисперсию коэффициентов регрессии:
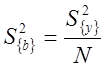 =
=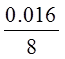 =
0,002
(13)
=
0,002
(13)
Определим доверительный интервал
![]() t
t![]() =12,71*0,045=0,57
(14)
=12,71*0,045=0,57
(14)
Так как все коэффициенты по абсолютной величине больше доверительного интервала, то все они значимы.
Приступим к нахождению максимального значения параметра оптимизации движением по градиенту.
Составим таблицу основных уровней и интервалов варьирования.
|
Факторы |
-1 |
основной |
+1 |
J |
|
Х1 |
0,25 |
0,625 |
1 |
0,375 |
|
Х2 |
0,05 |
0,345 |
0,64 |
0,295 |
|
X3 |
0,4 |
1,45 |
2,5 |
1,05 |
Основной уровень выбираем как центр области, так как не известно никакой дополнительной информации о лучших точках,
|
Коэф, |
-1,03 |
-0,62 |
-1,96 |
|
Jibi |
-0,386 |
-0,183 |
-2,058 |
|
Шаг |
5,15 |
3,1 |
9,8 |
|
Jibi/9,8 |
-0,039 |
-0,019 |
-0.21 |
Проведем мысленные опыты:
№ |
х1 |
х2 |
х3 |
1 |
0,586 |
0,326 |
1,24 |
|
2 |
0,546 |
0,308 |
1,03 |
|
3 |
0,507 |
0,289 |
0,82 |
|
4 |
0,467 |
0,27 |
0,61 |
|
5 |
0,428 |
0,252 |
0,4 |
Переводим кодированные значения факторов в натуральные:
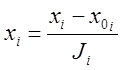 (15)
(15)
Для полученных значений находим значение параметра оптимизации по полученной ранее модели.
Таблица №6
№ |
х1 |
х2 |
х3 |
У |
1 |
-0,105 |
-0,063 |
-0,2 |
35,521 |
|
2 |
-0,21 |
-0,127 |
-0,4 |
36,06 |
|
3 |
-0,315 |
-0,19 |
-0,6 |
36,6 |
|
4 |
-0,42 |
-0,253 |
-0,8 |
37,139 |
|
5 |
-0,526 |
-0,316 |
-1 |
37,679 |
Сравнивая значения параметра оптимизации, полученные в мысленных опытах, и экспериментальные данные определяем максимальное значение параметра равным 38,545.
Ответ: наибольшее значение параметра оптимизации равное 38,545 достигается при значении факторов х1=0,25, х2=0,05, х3=0,4.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.