Вариант 2.
Задача 1.
Искомое сопротивление R (Ом) было измерено 15 раз и при этом получены результаты (см. таблицу 1). Необходимо определить среднюю квадратичную зависимость σА, интервал в котором находится значение измеряемого сопротивления с доверительной вероятностью Р1 и вероятную погрешность результата измерения ЕА для доверительной вероятности Р2.
|
R1 |
R2 |
R3 |
R4 |
R5 |
R6 |
R7 |
R8 |
R9 |
R10 |
|
340,2 |
353,1 |
347,3 |
355,6 |
344,6 |
350,1 |
348,2 |
364,9 |
359,4 |
344,6 |
|
R11 |
R12 |
R13 |
R14 |
R15 |
Р1 |
Р2 |
|
360,0 |
343,3 |
363,4 |
345,8 |
349,5 |
0,99 |
0,95 |
1. Найдем среднюю квадратичную зависимость σА. Для нормального закона распределения среднеквадратичное отклонение выражается следующей формулой:
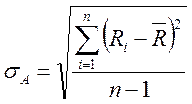
где n – количество измерений,
![]() -
среднее арифметическое, которое можно рассчитать, используя следующую формулу.
-
среднее арифметическое, которое можно рассчитать, используя следующую формулу.
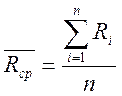
подставим численные значения и подсчитаем:
|
|
|
|
Определим абсолютную погрешность:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Определим интервал, в котором находится значение измеряемого сопротивления.
Найдём среднее арифметическое от среднего квадратического
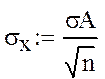
![]()
Тогда
|
|
|
|
3. Вычислим погрешность εА.
Выявляем промахи (исключаем все Δi ≥ Δmax). Промахов нет
Находим границы доверительного интервала Δ1
По таблице функции распределения Стьюдента при
Р1=0,99 Р2=0,95 n=15
t1=2.98 t2=2.15
Определим интервал:
|
|
|
|
|
|
|
|
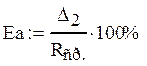
|
R =
Rср. ± D1 = |
![]()
Ответ: R=351.333 ± 5.931
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.