



ЗАДАНИЕ.
Цель работы: приобрести навыки в определении прямых и косвенных оценок качества САУ.
к=32
Т=0,15
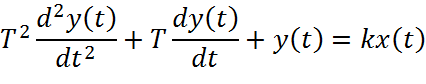
Привести дифференциальное уравнение к форме заменив
оператор дифференцирования 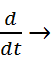 p.
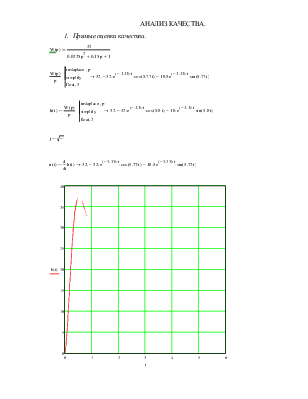
Определить передаточную функцию в изображениях по Лапласу. Построить переходный
процесс и АЧХ САУ.
p.
Определить передаточную функцию в изображениях по Лапласу. Построить переходный
процесс и АЧХ САУ.
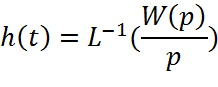
![]()
Построить графики функций. Все показатели определить на графиках.
АНАЛИЗ КАЧЕСТВА.
1. Прямые оценки качества.
|
|
|
|
|
|
|
|
|
|
|
|
hуст.=32
hmax=37,356
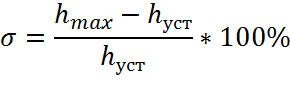
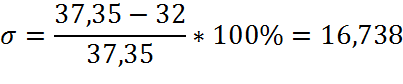
t1=0,375 с – время первого согласования
tн=0,5625 с – время нарастания переходного процесса
tт=1,292 с – время переходного процесса
Расчет для пяти процентной трубки
=32-32*EXP(-3,3*A1)*COS(5,77*A1)-18*EXP(-3,3*A1)*SIN(5,77*A1)
|
0,53 |
37,286 |
|
0,531 |
37,289 |
|
0,532 |
37,292 |
|
0,533 |
37,294 |
|
0,534 |
37,297 |
|
0,535 |
37,299 |
|
0,536 |
37,301 |
|
0,537 |
37,302 |
|
0,538 |
37,304 |
|
0,539 |
37,305 |
|
0,54 |
37,306 |
|
0,541 |
37,306 |
|
0,542 |
37,307 |
|
0,543 |
37,307 |
|
0,544 |
37,307 |
|
0,545 |
37,307 |
|
0,546 |
37,306 |
|
0,547 |
37,305 |
|
0,548 |
37,304 |
|
0,549 |
37,303 |
|
0,55 |
37,302 |
|
0,551 |
37,300 |
|
0,552 |
37,298 |
|
0,553 |
37,296 |
|
0,554 |
37,294 |
|
0,555 |
37,291 |
|
0,556 |
37,288 |
|
0,557 |
37,285 |
|
0,558 |
37,282 |
|
0,559 |
37,279 |
=32-32*0,025 31,2
=32+32*0,025 32,8
n=1 – полное колебание переходного процесса до вхождения в 5% трубку
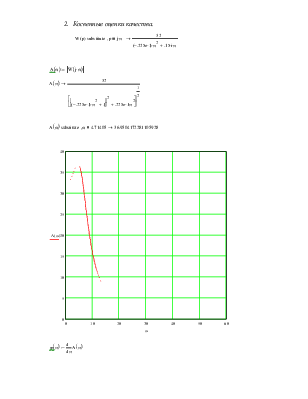
2. Косвенные оценки качества.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А(0)=32 – значение амплитуды выходной величины при нулевой частоте
![]() - максимальное
значение амплитуды
- максимальное
значение амплитуды
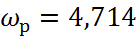 - резонансная частота
- резонансная частота
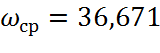 - частота среза
- частота среза
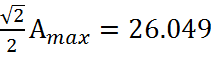 - полоса пропускания
частот
- полоса пропускания
частот
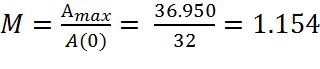 – показатель
колебательности
– показатель
колебательности
АНАЛИЗ УСТОЙЧИВОСТИ.
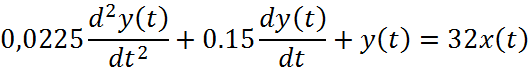
В операторной форме:
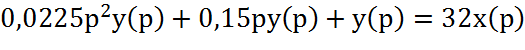
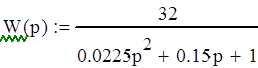
Решим характеристическое уравнение
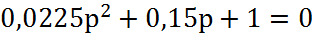
D=b2-4ac
D=(0.15)2-4*0.0225*1=0.0225-0.09=-0.0675, т.е. D<0
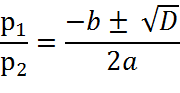
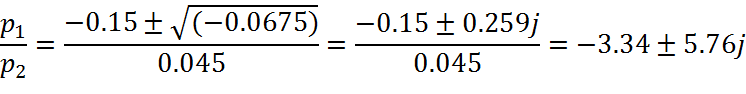
![]()
![]()
Сопряженные корни.
![]()
![]()
Следовательно, синусоида затухает и система является устойчивой.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.