Ознакомление с методом гармонической линеаризации нелинейностей и методами расчета параметров автоколебаний в нелинейных системах

Цель работы: ознакомится с методом гармонической линеаризации нелинейностей и методами расчета параметров автоколебаний в нелинейных системах.

Структурная схема системы:

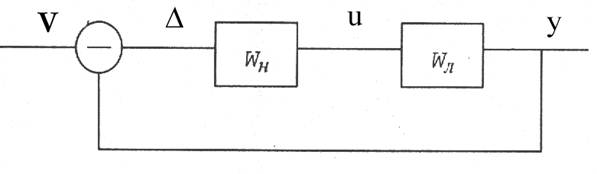
Передаточная функция линейной части:

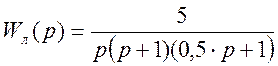
1. Зададим нелинейность типа «идеальное реле»:

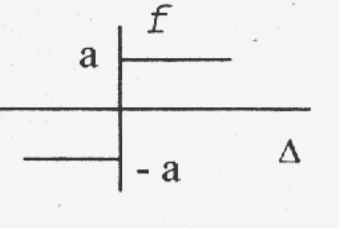
Проведем анализ системы методом Гольдфарба:

На комплексной плоскости построим АФХ линейной части и отрицательную обратную характеристику нелинейного элемента .

При движении по обратной частотной характеристике нелинейного элемента АФХ линейной части пересекается изнутри наружу. Система имеет устойчивые автоколебания с угловой частотой  и амплитудой .

2. Зададим нелинейность типа «реле с зоной нечувствительности»:

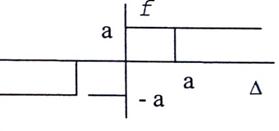
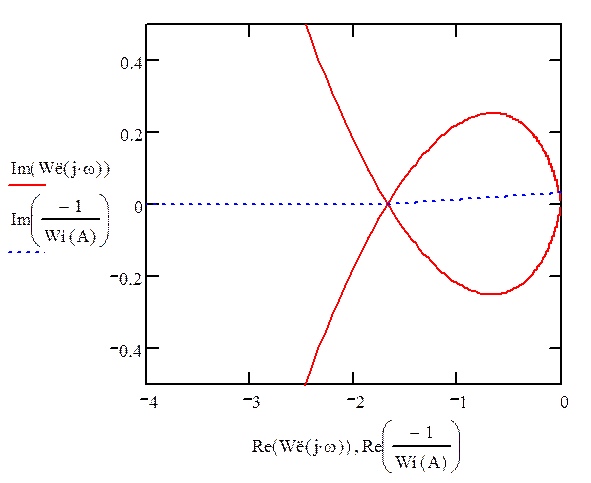
При движении по обратной частотной характеристике нелинейного элемента АФХ линейной части в точке (-1,8;0) пересекается изнутри наружу, следовательно, система имеет устойчивые автоколебания с угловой частотой  и амплитудой . А в точке (0,;0,05) обратная частотная характеристика нелинейного элемента пересекает АФХ линейной части снаружи вовнутрь, следовательно, система имеет неустойчивые автоколебания с угловой частотой  и амплитудой .

3. Зададим нелинейность типа «реле с гистерезисом»:

При движении по обратной частотной характеристике нелинейного элемента АФХ линейной части в точке (-2,85;-0,25) пересекается изнутри наружу, следовательно, система имеет устойчивые автоколебания с угловой частотой  и амплитудой .

4. Зададим нелинейность типа «зона нечувствительности»:

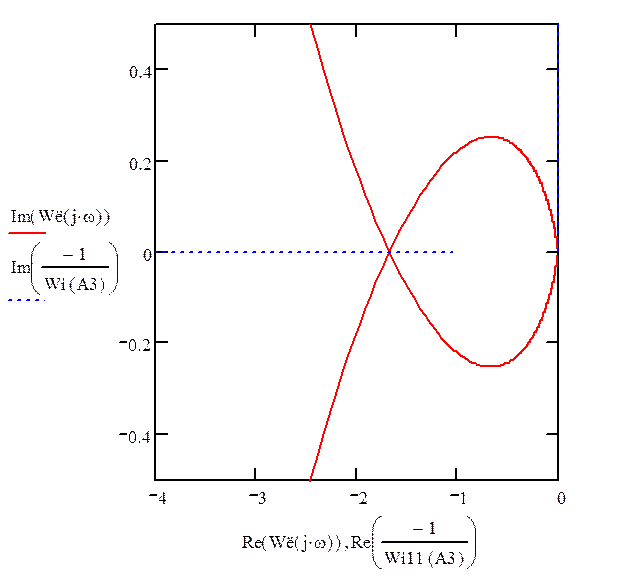
При движении по обратной частотной характеристике нелинейного элемента АФХ линейной части пересекается изнутри наружу. Система имеет устойчивые автоколебания с угловой частотой  и амплитудой .

Вывод: в ходе данной практической работы была исследована САУ, содержащая линейную и нелинейную части, методом гармонической линеаризации нелинейностей типа: идеальное реле, реле с зоной нечувствительности, реле с гистерезисом и зона нечувствительности. Для каждого типа нелинейности были определены устойчивые и неустойчивые автоколебания, а также их параметры: амплитуда и частота.