Наблюдение объектов при случайных помехах, страница 4

                                                A(t)               

             а)                                                     B(t)        

                                               

y(t)   I            -          K(t)        +          +              I/s              

         б)                                                     А(t)                 

                          C(t)                                      

 Рис.4.4. Структурные схемы непрерывного объекта (а) и фильтра Калмана (б).

При модальном управлении вектор состояния можно оценивать при помощи фильтра Калмана. Вся замкнутая система управления в целом описывается тогда уравнениями:

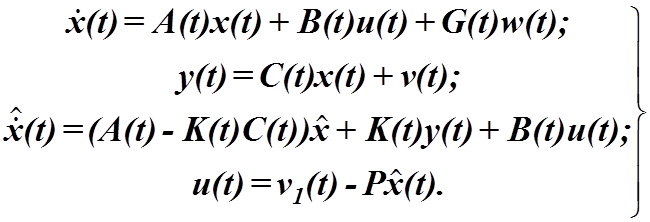         (4.41)

Под  понимается вектор задающих воздействий, а под Р- матрица преобразования регулятора.

Внешнее случайное воздействии и измерительный шум не оказывают влияния на устойчивость системы и при дальнейших преобразованиях они опущены.

Докажем теперь, что корни замкнутой системы совпадают с собственными значениями матриц  и   Введем вместо переменной  переменную  и после преобразований получим следующую систему уравнений:

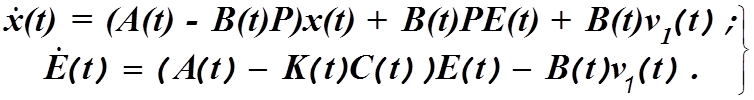    (4.42)

Система уравнений (4.41) имеет треугольную матрицу

            
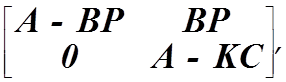
откуда следует, что характеристический полином этой системы

имеет корни, совпадающие с собственными числами указанных матриц. В последних выражениях, с целью упрощения записи, параметр t  опущен.

Полученный результат показывает, что если дело идет о смещении корней замкнутой системы к предписанным значениям, то наблюдающее устройство никак не нарушает этого процесса, а просто добавляет к имеющимся корням системы свои корни. Структурная схема всей системы управления, составленная по уравнениям  (4.41) показана на рис.4.5.

Сделаем в системе (4.41) эквивалентные преобразования. В третье уравнение системы вместо   подставим его значение   и в результате получим

          

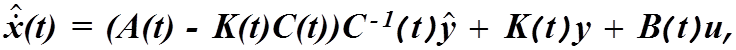
или

            

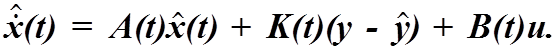
Преобразованная структурная схема системы, построенная по последнему выражению (рис.4.6) показывает, что фильтр Калмана представляет собой не что иное, как модель наблюдаемого объекта, дополненную звеном  Основная трудность в создании этого фильтра заключается именно в определении коэффициента

               Объект                                                                 V                                                                                                                                                                                                                                                                                                                   

                                                                                 

B(t)      +           +              I/s             C(t)         +            Y

                                                                                       

    G(t)                                    A(t)

 

    W

 

                                                        K(t)                                                                                                                                                                                                    

 B(t)          +          +                  I/s                           

 

                                                    

Фильтр Калмана         A(t)-K(t)C(t)  

 

u

 -P(t)

         Рис.4.5. Замкнутая система c наблюдающим устройством Калмана

Когда, действующие на объект случайные возмущения и ошибки измерения- белые шумы, коэффициент  можно расчитать по ранее выведенным уравнениям. Если действующие на объект возмущения w₁ (t) представляются “цветным шумом”, а ошибки измерения -“ белым шумом”, то по сравнению с предыдущим случаем дополнительных трудностей не возникает. Необходимо просто к уравнениям объекта добавить уравнение формирующего фильтра, предназначенного для получения “ цветного шума” из белого.

Исходный объект и формирующий фильтр образуют расширенный объект управления. Выходной сигнал формирующего фильтра с требуемой кривой спектральной плотности входного сигнала рассматривается как часть переменных состояния расширенного объекта. Таким образом, благодаря формирующему фильтру, задача сводится к прежнему случаю, когда возмущающие воздействия представляют собой “ белый шум”.

                                                                                                         

                                                    

B(t)          +       +            I/s               C(t)       +        +    

 G(t)                                 A(t)                          V  

                                                                                - 1         

W             Объект                                                              

K(t)  

B(t)         +        +           I/s            C(t)                          

Фильтр Калмана

                                   A(t)                             -P(t)          u

Рис.4.6.Система, эквивалентная, изображенной на рис.4.5.

Статистическая обработка информации, основанная на теории оптимальной фильтрации Калмана-Бьюси, предполагает техническую реализацию на базе цифровых ЭВМ. Следовательно, особый интерес в прикладных задачах имеет дискретная оптимальная фильтрация. Результаты непрерывной оптимальной фильтрации Калмана-Бьюси могут быть распространены на дискретные динамические системы [2,3]. Приведем без вывода уравнения дискретного оптимального фильтра Калмана-Бьюси.

Математическая модель обьекта:

  

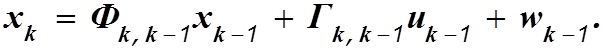
Математическая модель измерений:

 

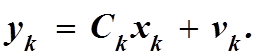
Уравнения фильтра:

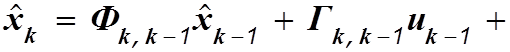
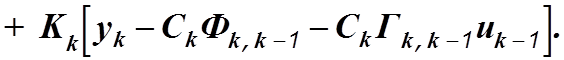
Оптимальный коэффициент усиления:

Априорная корреляционная матрица ошибок оценивания:

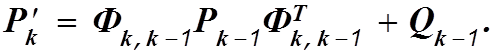
Апостериорная корреляционная матрица ошибок оценивания:

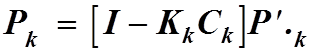
В приведенных уравнениях :

n-мерный вектор состояния;

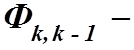переходная матрица состояния размерности ;

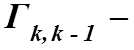матрица входного воздействия.