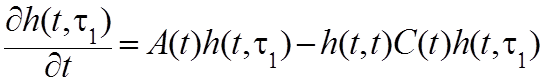Наблюдение объектов при случайных помехах, страница 3

                              (4.31)
Подставив (4.31) в (4.30), получим

 
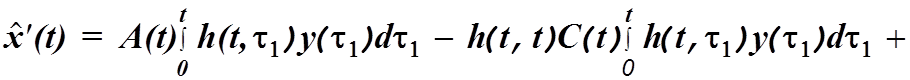
                                                                                        (4.32)
Подставив (4.29) в (4.31), найдем дифференциальное уравнение оптимальноготфильтра  Калмана - Бьюси:

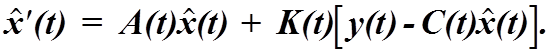                        (4.33)

Здесь функция  заменена на   для приведения к общепринятому обозначению.

Первый член в правой части последнего уравнения представляет собой априорную оценку вектора состояния, основанную только на уравнении объекта, а второй член-поправку к этой оценке, равную взвешенной разности между априорной оценкой   выходного сигнала и измеренным значением  этого сигнала. Детерминированный входной сигнал  влияет только на априорную оценку и его легко учесть, вводя в уравнение  (4.33) в качестве третьего члена   

4.3.2. Определение оптимального коэффициента усиления фильтра.

Линейная оптимальная фильтрация случайных процессов допускает векторное представление, при котором условие оптимальности рассматривается в соответствии с принципом ортогональных проекций.

 Если имеются два вектора, то их скалярное произведение запишется в виде       Скалярное произведение равно нулю при    Векторы   и     в этом случае называются ортогональными и записывается это следующим образом: .Допустим, что в некотором пространстве Н задана плоскость измерительных векторов   и в этом пространстве определен вектор (рис.4.3) ,который необходимо оценить, используя любой из векторов плоскости.

                      Обозначим проекции вектора   на плоскость  

                                  как    и назовем эту величину оценкой  век-     

                                         тора  . Ошибка оценивания запишется как     

Рис.4.3.К определению       Если  , то вследствие    того,                                      

   оценки вектора                       что перпендикуляр является кратчайшим расстоянием от точки до плоскости, ортогональность векторов и  плоскости  и является условием оптимальности оценки, что можно записать следующим образом

 

  

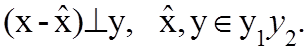
  Под оптимальным коэффициентом усиления подразумевается матрица  выполняющая роль весового множителя в поправочном члене уравнения Калмана. Так как  не зависит от добавляемого детерминированного сигнала в дальнейшем при определении оптимального коэффициента усиления будем использовать не измененное уравнение (4.32).

Определим ошибку оценивания следующим образом:

                                                                      (4.33)

Используя (4.29) и (4.33), преобразуем выражение

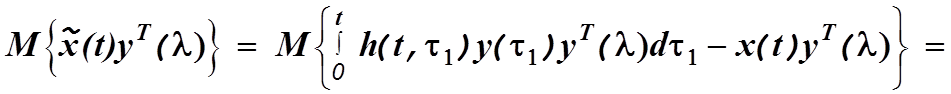
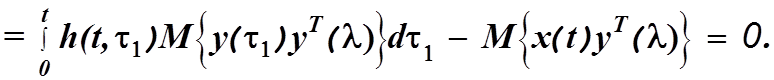         (4.34)

Равенство нулю этого выражения вытекает из уравнения Винера-Хопфа.

Левая часть уравнения (4.34)- скалярное произведение ошибки оценивания и измеренного вектора  Равенство нулю этого произведения показывает, что ошибка оптимального оценивания ортогональна пространству измерений  Поскольку  линейная функция  ошибка оценивания ортогональна также пространству т.е.

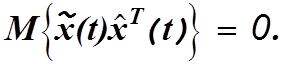                                                           (4.35)

Полагая в уравнении (4.34)  , после замены   получим

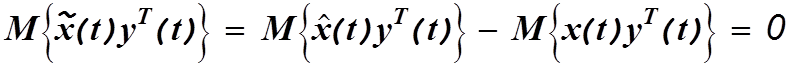
или

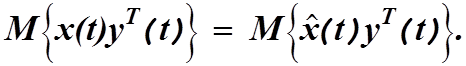                                  (4.36)

Подставив второе уравнение системы (4.21) в левую, а выражение (4.29) в правую части уравнения (4.36), найдем

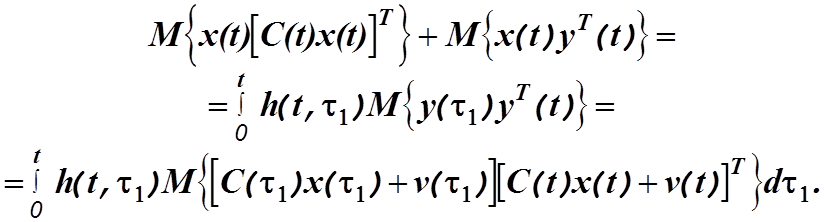
Учитывая, что корреляция между  и   отсутствует и корреляционная функция измерительного шума равна   получим

                       

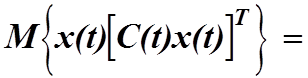
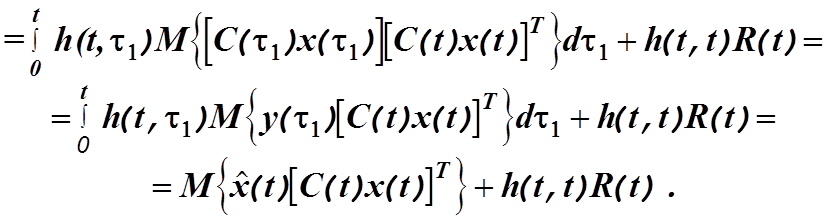
Здесь при последнем переходе было использовано уравнение (4.29). Перенося первый член из правой части в левую и используя уравнения (4.33) и (4.35), находим
 
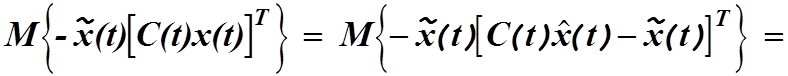
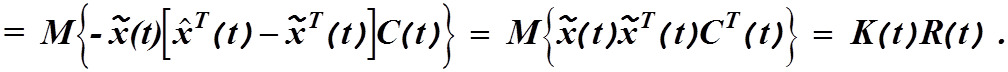                                                                                                                (4.37)

Здесь снова использовано обычное обозначение    

Введем в рассмотрение корреляционную матрицу ошибок оценивания

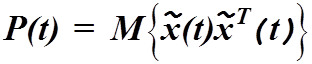               .                                          (4.38)  
Тогда на основании выражения  (4.37) можно записать

                                                 (4.39)
В правой части этого уравнения все величины, за исключением корреляционной матрицы ошибок оценивания, известны.

Корреляционная матрица ошибок оценивания определяется решением матричного уравнения Рикатти [2,3,4].
  

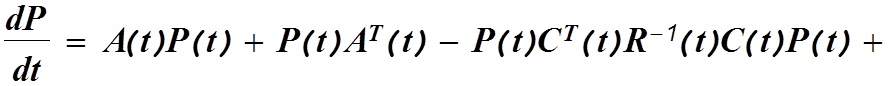
                                                                  (4.40)

В этом уравнении все коэффициенты- известные функции времени. Решая данное уравнение, находим корреляционную матрицу ошибок оценивания  , необходимую для вычисления по уравнению (4.39) оптимального коэффициента усиления  фильтра Калмана.
   4.3.3   Анализ уравнений оптимальной непрерывной фильтрации.

Полная система уравнений оптимальной непрерывной фильтрации включает в себя уравнения объекта (4.21), уравнение оптимальной фильтрации Калмана- Бьюси (4.32), уравнение для вычисления оптимального коэффициента усиления (4.39) и уравнение для вычисления корреляционной матрицы ошибок оценивания (4.40). Последние два уравнения определяют только вычислительные процедуры и влияния на динамику системы управления не оказывают.

Структурные схемы непрерывного объекта управления и соответствующего фильтра Калмана с учетом управляющего воздействия  приведены соответственно на рис.4.4,а,б. Формирование оптимального коэффициента усиления по уравнениям (4.39) и (4.40) на рисунках не отражено.

Нетрудно видеть, что структурная схема оптимального фильтра содержит в качестве составной части структурную схему объекта наблюдения, на которую действует “взвешенный” сигнал рассогласования между действительно измеренным значением   выходного сигнала и его прогнозированным значением 

“Взвешивание” производится звеном, передаточная функция    которого  равна оптимальному коэффициенту усиления фильтра. Это звено входит в замкнутый контур, так что устойчивость этого контура, т.е. устойчивость фильтра Калмана, зависит от корреляционных матриц   и   белых шумов, представляющих случайные воздействия на объект и ошибки измерения выходного сигнала. Фильтр устойчив, если его матрица   имеет собственные значения с отрицательными вещественными частями.

                 

     w(t)      G(t)                                                    n(t)       

 

u(t)                                                

       B(t)            +          +               I/s               C(t)       +              y(t)