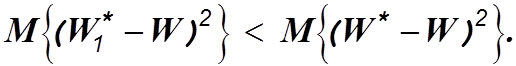Наблюдение объектов при случайных помехах, страница 2

                             (4.15)
Это неравенство показывает, что при любом достаточно малом по абсолютной величине отрицательном значении коэффициента a система, изображенная на рис.4.2 будет лучше предполагаемой оптимальной при выполнении неравенства (4.13). Если выбрать неравенство, противоположное неравенству (4.13), то аналогичное доказательство можно провести для достаточно малого положительного числа a.

Итак, доказано, что если класс R, в котором ищется оптимальная система, является линейным пространством, то необходимым и достаточным условием оптимальности системы по критерию минимума СКО является выполнение условия (4.12).

4.2.Интегральное уравнение Винера-Хопфа.

Интегральное уравнение Винера-Хопфа для многомерной нестационарной  линейной динамической системы (ДС) можно представить в обобщенном виде как линейный фильтр, на вход которого поступает r-мерный вектор наблюдения , а на выходе линейного фильтра вырабатывается оценка  n-мерного вектора состояния   Пусть Н и Н^*- соответственно операторы оптимального и неоптимального линейных фильтров; и  -соответственно оптимальная и неоптимальная оценки вектора состояния   Тогда можно записать

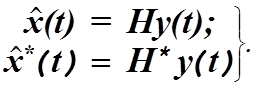                                                                (4.16)
Обозначив матричные  импульсные переходные характеристики оптимального и неоптимального операторов как  и  , получим

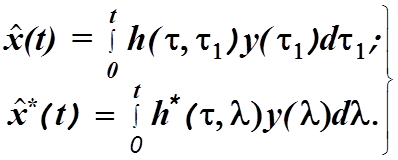                                              (4.17)
Примем в качестве критерия оптимальности фильтрации критерий минимума СКО, который может быть записан в виде

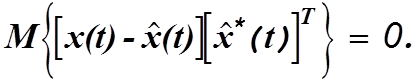                                             (4.18)

Подставим последнее выражение в (4.17) и после преобразований получим

           

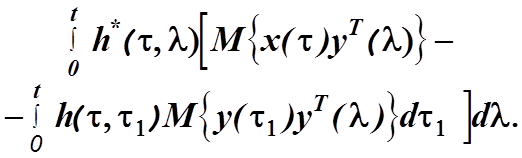
Для любой матричной импульсной переходной характеристики  нестационарного линейного фильтра условие оптимальности (4.18) будет выполняться при равенстве нулю выражения в квадратных скобках. Введем обозначения:   

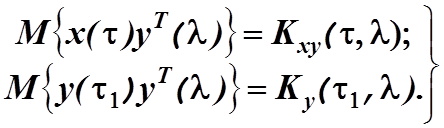                                       (4.19)
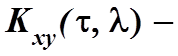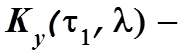В этом выражении  матричная взаимная ковариационная функция нестационарных многомерных векторов  и    матричная ковариационная функция нестационарного случайного многомерного вектора    С учетом (4.19) из равенства нулю указанного выражения в скобках  получим

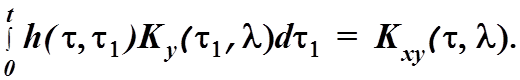                            (4.20)

Уравнение  (4.20) является обобщенным интегральным уравнением Винера-Хопфа для нестационарного многомерного линейного физически возможного фильтра.

Решение уравнения (4.20)   позволяет определить оптимальную матрицу импульсных переходных характеристик   нестационарного линейного фильтра. Решение интегрального уравнения Винера-Хопфа представляет собой чрезвычайно трудоемкую задачу даже с применением современных цифровых машин, что ограничивает практический синтез нестационарных фильтров. В связи с этим практическое применение теории оптимальной фильтрации Винера целесообразно в основном для одномерных  случайных  процессов. Практическая реализация фильтра Винера затруднена, так как до окончания решения интегрального уравнения нельзя оценить структуру фильтра. Аналитический расчет фильтров Винера для систем высокого порядка очень трудоемок, а использование ЭВМ ограничено в связи с синтезом оптимального фильтра в частотной области изменения аргумента, что наиболее существенно при решении конкретных технических задач.

4.3 .Уравнения нестационарной фильтрации Калмана-Бьюси.

Пусть требуется оценить вектор состояния  многомерного линейного объекта с переменными параметрами, описываемого уравнениями

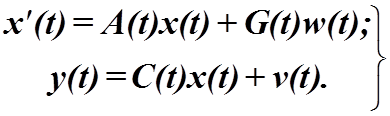                                             (4.21)

Здесь - действующее на объект случайное возмущение типа “белый шум” с нестационарной матричной корреляционной функцией

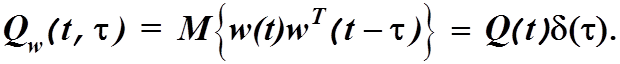              (4.22)

Ошибки измерения также предполагаются в виде нестационарного “белого шума” с матричной корреляционной функцией

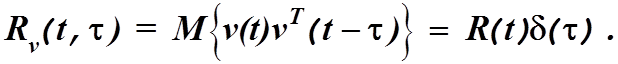              (4.23)

Предусматриваемое формулами (4.22) и (4.23) усреднение необходимо проводить по ансамблю реализаций (нестационарные матричные корреляционные функции имеют смысл только в этом случае).

Корреляционная матрица измерительного шума  предполагается в дальнейшем положительно-определенной. Диагональные члены  этой матрицы представляют собой дисперсии измерительных шумов в -ых каналах измерения. Вследствие отсутствия корреляции между измерительными шумами в разных каналах недиагональные члены матрицы  равны нулю.

4.3.1.  Вывод дифференциального уравнения оптимального фильтра Калмана-Бьюси.

Продифференцируем полученное выше уравнение Винера-Хопфа по времени и обратимся к рассмотрению его правой части

 .
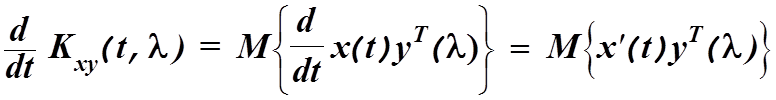Подставив сюда выражение для  из первого уравнениясистемы (4.21) и принимая обычное предположение об отсутствии корреляции между измеряемым вектором   и белым шумом , получим

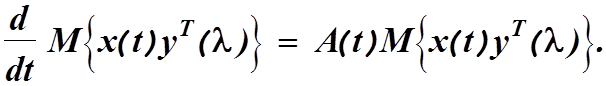                (4.24)

В соответствии с правилом дифференцирования под интегралом по параметру для левой части уравнения Винера-Хопфа можно записать

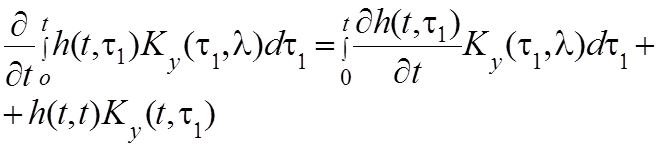                    (4.25)

                  
Входящая в состав этого выражения матрица 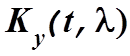 определяется как

                 
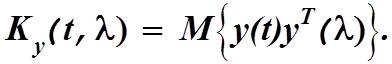
Подставляя сюда вместо его значение из второго уравнения системы (4.21) и принимая предположение о некоррелированности измерительных шумов и измеряемых параметров, получим

         

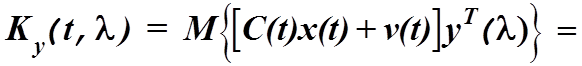
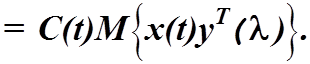                                                         (4.26)

Это выражение представляет собой правую часть уравнения Винера-Хопфа, умноженную на матрицу выхода а выражение (4.24)- эту же правую часть, умноженную на матрицу системы  Подставляя в уравнение (4.24) вместо 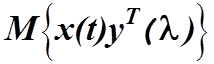 левую часть уравнения (4.20), находим
 

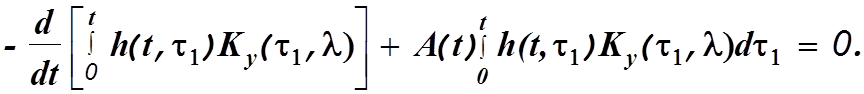
Заменим первый член этой формулы выражением (4.25), а в последнем члене полученного уравнения матрицу 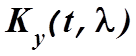- выражением (4.26), получим
 
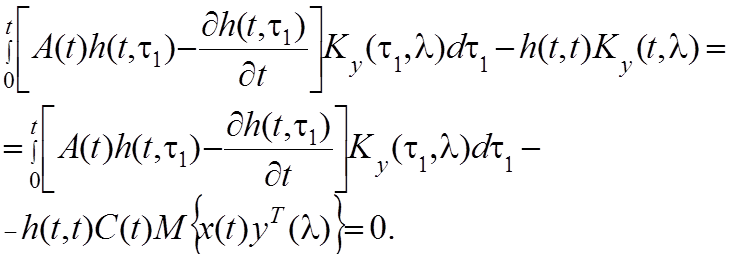
Заменяя в последнем члене этого уравнения 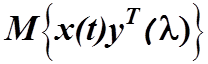  левой частью уравнения (4.20), приходим к уравнению
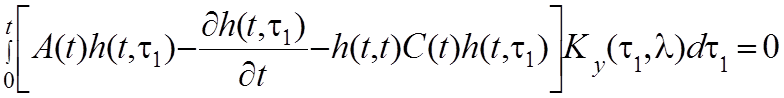    (4.27)
 
Поскольку 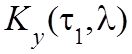 - произвольная функция, то уравнение (4.27) будет удовлетворяться только при равенстве нулю выражения в квадратных скобках. Следовательно,

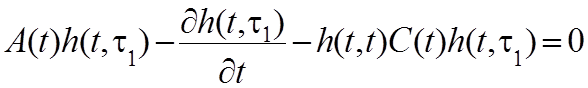                         (4.28)
Фильтр с оптимальной  импульсной  переходной матрицей  дает в качестве оптимальной оценки вектора состояния в конечный момент t выражение

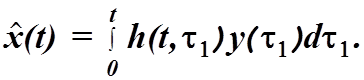                                                        (4.29)
Дифференцируя это выражение по t, получим

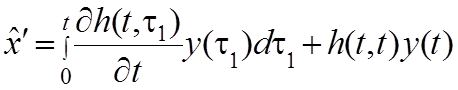                                          (4.30)
Из уравнения (4.28) находим выражение для частной производной