4. Что такое простой полюс функции.
5. В каком случае можно говорить о полюсах функции.
ЛЕКЦИЯ 5
Цель: Изучить применение вычетов функции.
Задачи:
1. Изучить понятие вычета функции.
2. Изучить поведение функции в окрестности изолированной особой точке.
3. изучить применение вычетов.
Вычетом
функции ![]() в изолированной точке
в изолированной точке ![]() называется интеграл вида:
называется интеграл вида:
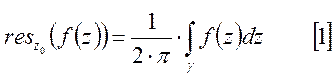
который,
берется по замкнутому контуру, охватывающему точку ![]() и
не содержащему внутри других особых точек и непроходящему через такие точки.
и
не содержащему внутри других особых точек и непроходящему через такие точки.
Теорема о вычетах.
Пусть
![]() регулярная аналитическая функция
внутри контура Г за исключением находящихся внутри Г особых точек
регулярная аналитическая функция
внутри контура Г за исключением находящихся внутри Г особых точек ![]() и непрерывна на всей области Г.
Тогда интеграл по области Г равен сумме вычетов в этих особых точках умноженный
на
и непрерывна на всей области Г.
Тогда интеграл по области Г равен сумме вычетов в этих особых точках умноженный
на ![]() .
.
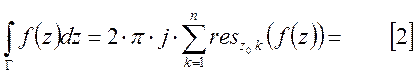
Доказательство.
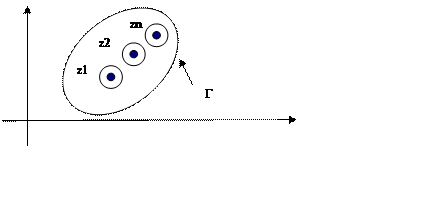
Пусть
внутри Г, расположены точки ![]() . Окружим каждую
точку малым контуром
. Окружим каждую
точку малым контуром ![]() так, чтобы каждая
так, чтобы каждая ![]() заключала внутри себя только одну
точку z, целиком лежащую внутри контура и не
пересекается с другими
заключала внутри себя только одну
точку z, целиком лежащую внутри контура и не
пересекается с другими ![]() .
.
По теореме Коши:
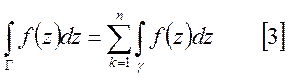
в последнем равенстве для каждого интеграла правой части справедливо равенство:
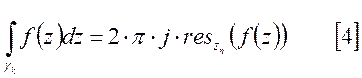
Подставив [4] в [3] получаем [2].
В
изолированной особой точке однозначного характера ![]() вычет
в ней равен коэффициенту
вычет
в ней равен коэффициенту ![]() ряда Лорана
функции
ряда Лорана
функции ![]() при
при ![]() .
.
Теорема.
Пусть
![]() - простой полюс для функции
- простой полюс для функции 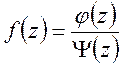 , где
, где ![]() -
простой ноль для
-
простой ноль для ![]() , то есть
, то есть ![]() . Тогда справедливо равенство:
. Тогда справедливо равенство:
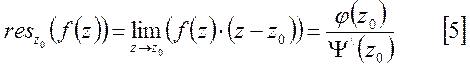 .
.
Доказательство.
Если ![]() - простой полюс, то ряд Лорана для
- простой полюс, то ряд Лорана для ![]() имеет следующий вид:
имеет следующий вид:
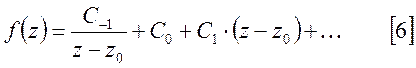
Умножая
обе части [6] на![]() и переходя к пределу
получаем:
и переходя к пределу
получаем:
![]()
так
как ![]() - простой ноль для функции
- простой ноль для функции ![]() , а
, а ![]() ,
так как
,
так как ![]() , тогда для предела [7] справедливо
равенство:
, тогда для предела [7] справедливо
равенство:
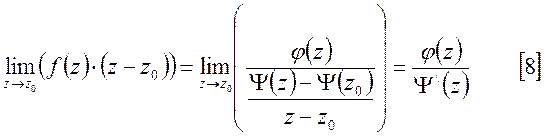
подставив [8] в [7] получаем [6].
Если ![]() - порядка n, для функции
- порядка n, для функции ![]() , тогда вычет этой функции
в точке
, тогда вычет этой функции
в точке ![]() будет иметь следующий вид:
будет иметь следующий вид:
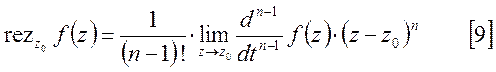
Для
вычисления вычета в особой точке ![]() имеет место формула:
имеет место формула:
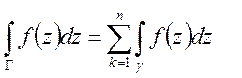
при этом функцию следует разложить в ряд Лорана.
Рассмотрим
поведение регулярной функции ![]() в окрестностях
в окрестностях ![]() бесконечно удаленной точки
бесконечно удаленной точки ![]() . Примем
. Примем 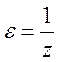 .
Сама точка
.
Сама точка ![]() переходит в
переходит в ![]() .
.
![]() называется регулярной в
бесконечности
называется регулярной в
бесконечности ![]() , если преобразованная функция
, если преобразованная функция
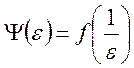 регулярна в точке
регулярна в точке ![]() .
.
Регулярная
функция ![]() в точке
в точке ![]() разлагается
в ряд Тейлора и имеет следующий вид:
разлагается
в ряд Тейлора и имеет следующий вид:
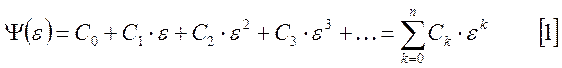
Возвращаясь
в разложении [1] к ![]() получаем разложение в
точке
получаем разложение в
точке ![]() равной бесконечности:
равной бесконечности:
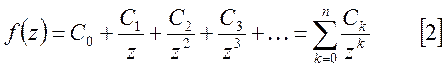
Бесконечно
удаленная точка ![]() , может быть изолированной
точкой однозначного характера, тогда разложение функции в окрестности точки
, может быть изолированной
точкой однозначного характера, тогда разложение функции в окрестности точки ![]() имеет вид:
имеет вид:
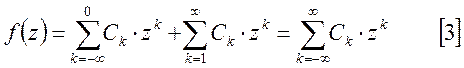
В
этом случае главной частью разложения [3] является 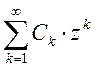 ,
а правильной частью -
,
а правильной частью - 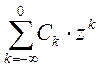 .
.
Определим
коэффициенты ряда [3]. Для этого рассмотрим окружность ![]() ,
удовлетворяющую условию
,
удовлетворяющую условию ![]() .
. ![]() . Окружность обходит в положительном
направлении по отношению к часовой стрелки. Заменив в [3]
. Окружность обходит в положительном
направлении по отношению к часовой стрелки. Заменив в [3] ![]() на
на ![]() и
умножая на
и
умножая на 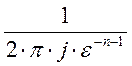 и проинтегрировав по Г, получаем:
и проинтегрировав по Г, получаем:
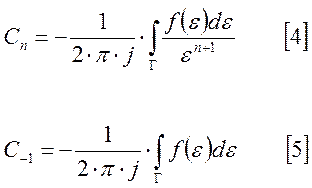
Вычетом
функции ![]() в точке
в точке ![]() является
взятый со знаком « - » коэффициент
является
взятый со знаком « - » коэффициент ![]() при
при ![]() в разложении [3].
в разложении [3].
![]()
Теорема.
Пусть
![]() - регулярная функция, имеющая в
расширенной плоскости комплексных переменных только изолированные особые точки,
тогда сумма вычетов
- регулярная функция, имеющая в
расширенной плоскости комплексных переменных только изолированные особые точки,
тогда сумма вычетов ![]() во всех особых точках
равна 0.
во всех особых точках
равна 0.
Доказательство.
Пусть
Г – окружность в которой находится изолированная особая точка z с радиусом ![]() :
: ![]() .
Радиус настолько большой, что все особые точки
.
Радиус настолько большой, что все особые точки ![]() находятся
внутри этой окружности. Согласно теореме о вычетах:
находятся
внутри этой окружности. Согласно теореме о вычетах:
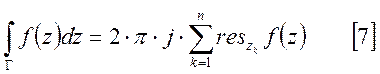
Г –
обходит точки ![]() против часовой стрелки,
тогда [7] примет вид:
против часовой стрелки,
тогда [7] примет вид:
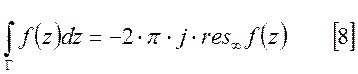
Подставим [7] в [8], тогда:
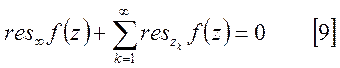
Вычислить
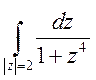 .
.
Функция
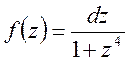 имеет 4 простых полюса:
имеет 4 простых полюса:
![]()
Точка
![]() является правильным нулем функции
является правильным нулем функции ![]() . Разложение функции
. Разложение функции ![]() имеет вид:
имеет вид:
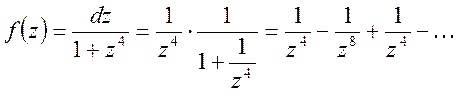
![]() , то
, то 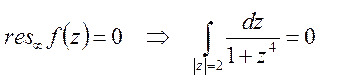 .
.
Пример:
Функция
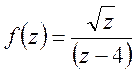 . Найти вычет функции в замкнутом
контуре
. Найти вычет функции в замкнутом
контуре ![]()
Г – окружность.
Найдем полюсы:
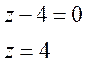
- простой полюс.
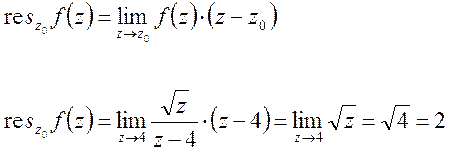
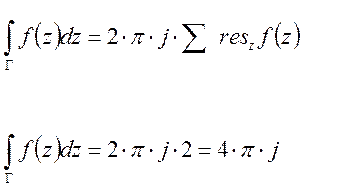
Пример 2.
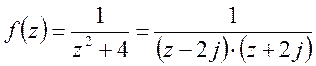
2
простых полюса: 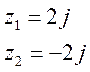
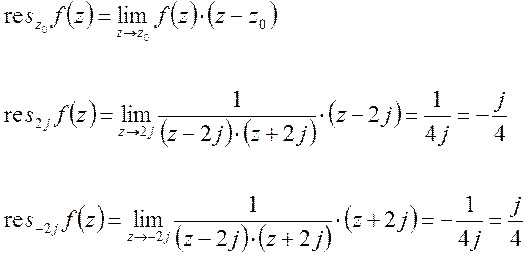
Интегралы вида:
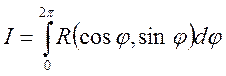 ,
,
где R – рациональная функция от синуса и косинуса, сводится к решению интеграла
по окружности ![]() , где z заменяют на
, где z заменяют на ![]() , тогда по формуле Эйлера:
, тогда по формуле Эйлера:
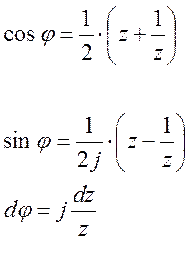
Вопросы для самоконтроля.
ЛЕКЦИЯ 6.
Цель. Изучить построение оптимальных систем управления.
Задачи:
1. Изучить теорию построения оптимальных систем.
2. Изучить методы построения оптимальных систем.
САУ, обеспечивающие наилучшее или оптимальное значение какого-либо показателя качества системы, называются оптимальными САУ. Величина, характеризующая качество системы, ее минимальное или максимальное значение называют критерием оптимальности. На параметры системы могут накладываться какие-либо ограничения. Их также необходимо учитывать при определении наилучшего значения параметра оптимизации. В случае, если при синтезе САУ необходимо определить несколько наилучших значений параметров оптимизации в этом случае поступают одним из 2 способов:
1. Из всех параметров оптимизации составляют один интегральный параметр и для него решают оптимизационную задачу.
2. Для каждого параметра оптимизации ищут варианты решения. При этом остальные параметры используют в качестве ограничений. Из всех полученных решений выбирают одно наиболее удовлетворяющее поставленным требованиям.
1. В этом случае САУ оптимизируют на основе подбора и использования существующих методов анализа систем. В данном случае рассматриваются различные варианты систем с различными параметрами и законами регулирования. Затем расчеты сравниваются, и выбирается вариант, для которого принятый критерий имеет максимальное или минимальное значение.
2. Заключается в непосредственном определении оптимальной системы. Здесь существует 2 способа:
- задается структура системы и требуется найти оптимальное значение ее параметров, которые обеспечивают экстремумы выбранного критерия.
- система считается полностью неизвестной и требуется определить ее характеристики, обеспечивающие достижение экстремума критерия, идеального из всех числовых значений параметров.
Чаще всего значение критерия оптимизации определяется не текущим состоянием объекта, а его поведение в течение всего процесса управления. Поэтому критерий оптимальности можно представить в виде:
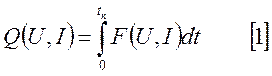 ,
,
где:
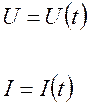
В
общем случае ![]() - есть вектора:
- есть вектора:
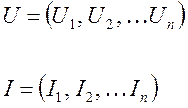
![]() - время переходного процесса
системы.
- время переходного процесса
системы.
При
решении задач оптимизации на величину выходного параметра ![]() и управляющего воздействия
и управляющего воздействия ![]() могут накладываться некоторые
ограничения, которые можно записать в виде следующего неравенства:
могут накладываться некоторые
ограничения, которые можно записать в виде следующего неравенства:
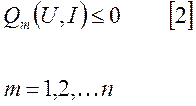
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.