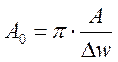 . Если относительная амплитуда
используется при построении графика спектра для периодической функции с
периодом Т, тогда вместо графика амплитудного спектра
. Если относительная амплитуда
используется при построении графика спектра для периодической функции с
периодом Т, тогда вместо графика амплитудного спектра ![]() получаем
график средней плотности амплитуды:
получаем
график средней плотности амплитуды:
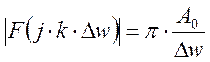 .
.
В
случае при ![]() , функция
, функция ![]() представляет
собой спектральную плотность:
представляет
собой спектральную плотность:

![]() - бесконечно малое приращение
амплитуды.
- бесконечно малое приращение
амплитуды.
Аргумент
спектральной плотности ![]() характеризует
начальную фазу гармоники, а функция:
характеризует
начальную фазу гармоники, а функция:
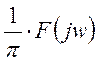 - относительную амплитуду этих
гармоник.
- относительную амплитуду этих
гармоник.
Функция:
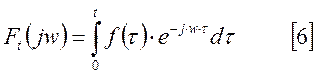
называется текущей спектральной характеристикой и используется при исследовании реальных процессов. В этом случае момент начала процесса известен заранее, и его можно определить как нулевой. При этом преобразование Фурье имеет вид:
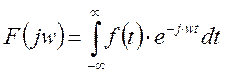
На
интервале ![]() .
.
Наблюдение ведется на конечном промежутке времени, следовательно, верхний предел интеграла можно взять t. В результате получаем выражение для текущей спектральной характеристики:
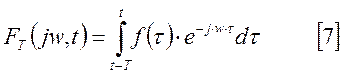
Полученное выражение называется мгновенной спектральной характеристикой и используется в тех случаях, когда исследуется влияние на функцию не на всем интервале наблюдения, а лишь в момент предшествующий рассматриваемому явлению.
Найдем взаимосвязь между двумя последними выражениями. Для этого представим мгновенную спектральную плотность в виде:
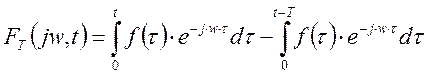
в
результате получим разность 2 текущих спектров. Обозначим ее через ![]() .
.
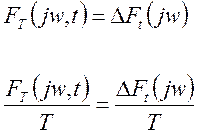
Когда
![]()
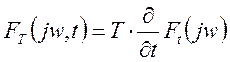
![]()
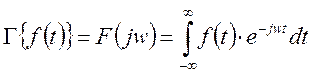 - преобразование Фурье.
- преобразование Фурье.
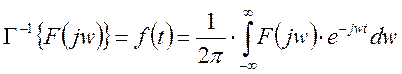 - обратное преобразование Фурье.
- обратное преобразование Фурье.
- свойство линейности.
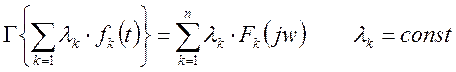
Линейной комбинации функций соответствует комбинация спектральных характеристик этих функций. Обратное преобразование Фурье от линейных комбинаций спектральных функций имеет вид:
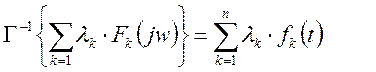
- свойство дифференцирования.
Спектр
производной функции определяется как спектр исходной функции умноженной на ![]()
![]() .
.
-свойство интегрирования.
Спектр
от интеграла некоторой функции ![]() на интервале
на интервале ![]() определяется как спектр исходной
функции, деленной на
определяется как спектр исходной
функции, деленной на ![]() :
:

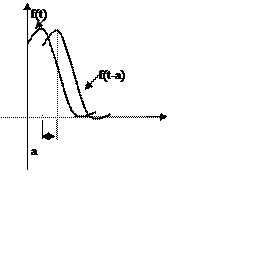
-спектр смещенной функции.
![]()
Спектр
смещенной функции равен спектру исходной функции умноженной на ![]() , где
, где ![]() -
смещение функции.
-
смещение функции.
-изменение масштаба.
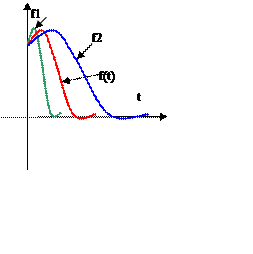
(Сжатие
или растяжение). Рассмотрим функцию ![]() . Построим график
функции:
. Построим график
функции:
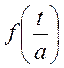
если 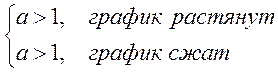
В этом случае:
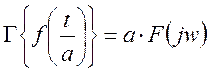
Сжатие
исходного сигнала на величину ![]() по времени t приводит к расширению спектра в
по времени t приводит к расширению спектра в ![]() раз
по частоте.
раз
по частоте.
-распределение энергии по гармоникам непериодического сигнала:
Найдем спектр от произведения 2 функции:
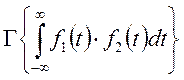
Если
заданы 2 функции ![]() , спектры которых
соответственно равны:
, спектры которых
соответственно равны:

то спектр от произведения этих функций будет равен:
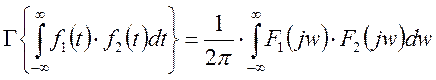
в
случае если ![]() , то спектр равен:
, то спектр равен:
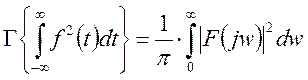
Где ![]() - энергетическая спектральная
характеристика.
- энергетическая спектральная
характеристика.
-интеграл свертки.
Рассмотрим
![]() и
и ![]() на
интервале
на
интервале ![]() . Функция:
. Функция:
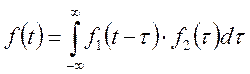
называется сверткой функции и обозначается:
![]()
Спектр от свертки функций определяется как произведение спектральных характеристик этих функций:
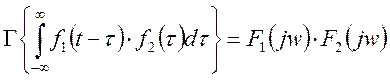
-спектр от произведения двух функций
Вопросы для самоконтроля.
1. Понятие спектра.
2. Свойства непрерывного спектра.
3. Понятие спектральной характеристики.
4. Спектры зависящие от времени.
ЛЕКЦИЯ 4
Цель. Изучить теорию о вычетах функции.
Задачи:
1. Рассмотреть разложение функции в ряд Лорана.
2. Изучить свойства рядов Лорана.
3. Изучить классификацию изолированных особых точек.
Теорема Лорана.
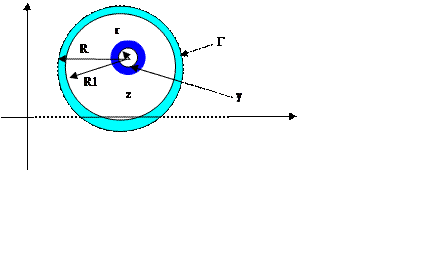
При исследовании поведения регулярной функции в окрестностях изолированной особой точки, требуется разложить ее в ряд Лорана в кольце:
![]()
Если ![]() регулярная аналитическая функция в
кольце [1], то всюду в этом кольце она раскладывается в ряд:
регулярная аналитическая функция в
кольце [1], то всюду в этом кольце она раскладывается в ряд:

![]() - простой замкнутый контур,
окружающий точку
- простой замкнутый контур,
окружающий точку ![]() и расположенный в кольце
и расположенный в кольце ![]() .
.
Доказательство.
Пусть
z – фиксированная произвольная точка в кольце ![]() . Выберем радиусы окружностей:
. Выберем радиусы окружностей:
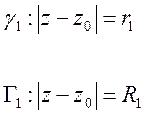
так, что:
![]()
Тогда
значение функции ![]() можно представить с
помощью интегральной формы Коши:
можно представить с
помощью интегральной формы Коши:

Множитель
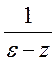 представим в виде:
представим в виде:

Ряд
[4] равномерно сходится по ![]() на окружности Г.
Подставим [4] в [3] и интегрируя почленно получим:
на окружности Г.
Подставим [4] в [3] и интегрируя почленно получим:
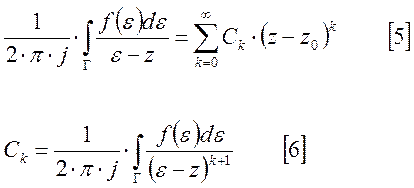
Множитель
 в интеграле по
в интеграле по ![]() представим в виде:
представим в виде:
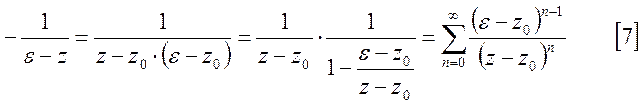
Ряд
[7] равномерно сходится по ![]() на окружности
на окружности ![]() . Подставим [7] в [3]и интегрируя
почленно получим:
. Подставим [7] в [3]и интегрируя
почленно получим:
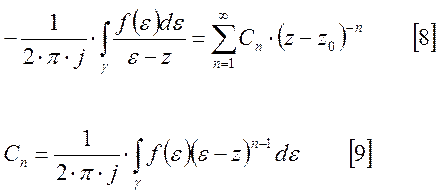
Заменяя в [8] n на k и объединяя два ряда [8] и [5] получим разложение вида [2].

1. Ряд Лорана представляет собой сумму 2 функциональных рядов:

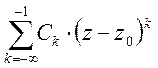 - главная часть
- главная часть
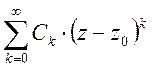 - правильная часть
- правильная часть
2. Ряд Лорана абсолютно сходится всюду в кольце сходимости:
![]()
Главная и правильная части являются рядами по степеням:
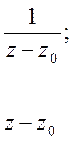
3. Ряд Лорана сходится абсолютно и равномерно в любом замкнутом кольце, расположенным внутри кольца сходимости, то есть для всех z, удовлетворяющих условию:
![]()
4. Ряд Лорана можно интегрировать почленно по любому контуру целиком, лежащим внутри кольца сходимости и дифференцировать его внутри кольца сколь угодно раз.
Пусть
![]() регулярная аналитическая функция в
некоторой окрестности точки
регулярная аналитическая функция в
некоторой окрестности точки ![]() , то есть при
, то есть при ![]() , а в самой точке
, а в самой точке ![]() функция
функция ![]() либо
не аналитична, либо не определена, тогда
либо
не аналитична, либо не определена, тогда ![]() является
особой изолированной точкой.
является
особой изолированной точкой.
Функцию
![]() в окрестности точки
в окрестности точки ![]() , можно разложить в ряд Лорана:
, можно разложить в ряд Лорана:
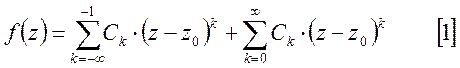
Ряд
[1] используется для классификации особых точек однозначного характера. Если
все коэффициенты ![]() главной части ряда при
всех k<0 равны 0, то
главной части ряда при
всех k<0 равны 0, то ![]() является
устранимой особой точкой и тогда:
является
устранимой особой точкой и тогда:
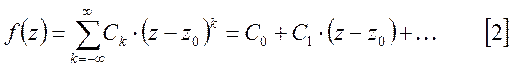
Если
в главной части ряда [1] имеется лишь конечное число отличных от 0
коэффициентов, то и в этом случае ![]() является полюсом,
а
является полюсом,
а
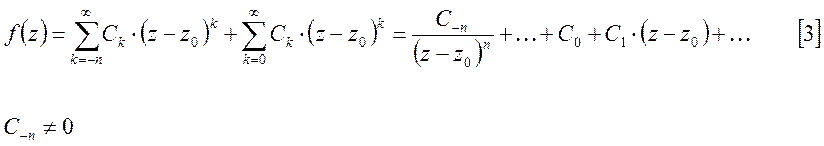
Степень
разложения разности ![]() «n» является порядком полюса.
«n» является порядком полюса.
Исследуем
связь между полюсом функции ![]() и нулем функции
и нулем функции 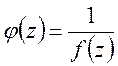 .
.
Точка
![]() называется правильным полюсом
функции
называется правильным полюсом
функции ![]() . Если
. Если ![]() регулярна
в точке
регулярна
в точке ![]() , а
, а ![]() .
.
Ряд Тейлора в окрестности нуля имеет вид:
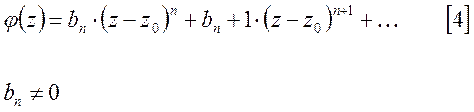
При n=1, полюс называется простым.
Теорема.
Для
того, чтобы точка ![]() была полюсом порядка n для функции
была полюсом порядка n для функции ![]() необходимо и достаточно,
чтобы она была нулем кратности n для функции
необходимо и достаточно,
чтобы она была нулем кратности n для функции 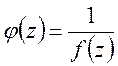 .
.
Доказательство.
Пусть
![]() является полюсом порядка n для
является полюсом порядка n для ![]() при:
при:
![]()
Функцию
![]() представим в виде :
представим в виде :
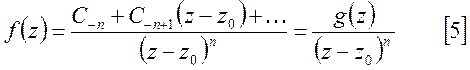 ,
,
где ![]() - регулярная функция в точке
- регулярная функция в точке ![]() , причем:
, причем:
![]() .
.
Функция
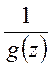 также регулярна в точке
также регулярна в точке ![]() и коэффициенты ее разложения находим,
используя правило дифференцирования. В итоге получим:
и коэффициенты ее разложения находим,
используя правило дифференцирования. В итоге получим:
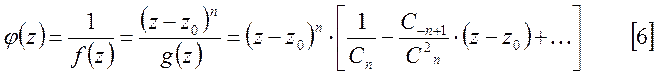
Из
этого выражения видно, что ![]() является нулем
кратности n для функции
является нулем
кратности n для функции ![]() .
.
Согласно [4] получим:
![]() ,
,
где ![]() регулярна в точке
регулярна в точке ![]() :
:
![]()
Функция
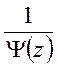 также регулярна в точке
также регулярна в точке ![]() .
.
Найдем коэффициенты разложения этой функции, используя правило дифференцирования:
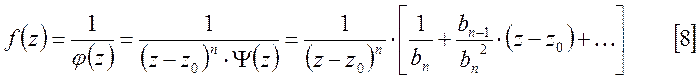 .
.
Из
[8] видно, что ![]() является полюсом порядка n для функции
является полюсом порядка n для функции ![]() .
.
Вопросы для самоконтроля.
1. Для чего используется разложение функции в ряд Лорана.
2. Свойства ряда Лорана.
3. Что такое полюс функции.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.