Математическое описание сигналов различного типа. Разложение сигнала по системе ортогональных и ортонормальных функций. Интеграл Фурье. Разложение функции в ряд Лорана, страница 2

Получим .

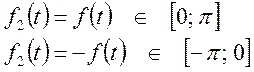
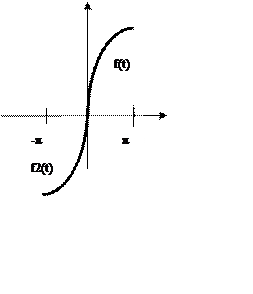
 будет нечетной на промежутке , тогда к этой функции можно применить разложение вида:

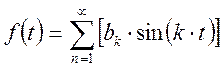
3.  Случай произвольного промежутка.

, где l – произвольное число. Разложим в ряд Фурье  данную функцию. Введем следующую замену:

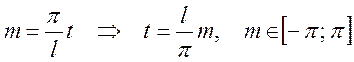
Тогда разложение будет иметь вид:

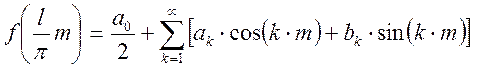, где

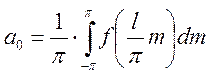
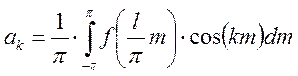
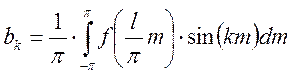
Произведя обратную замену и учитывая, что

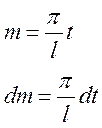
Тогда:

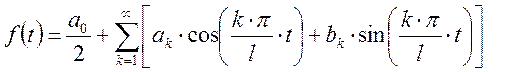
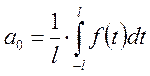
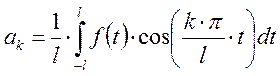
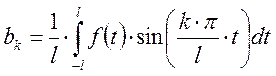
4. Случай произвольного половинного промежутка

Допустим  задана на промежутке . Вводи замену:

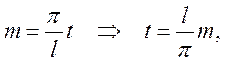
если t=0, то m=0

если t=l, то m=π.

Тогда справедливо выражение:

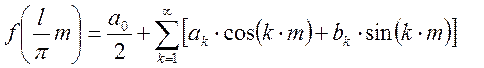
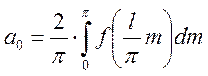
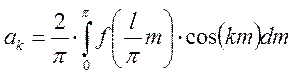
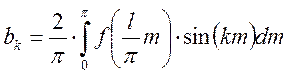
Произведя обратную замену :

Комплексная форма ряда Фурье.

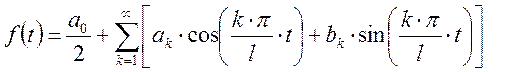
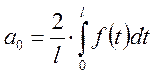
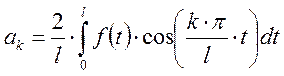
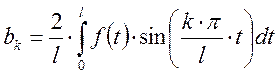
Рассмотрим функцию .

 

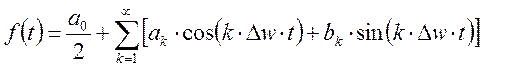
Разложим синус и косинус по формуле Эйлера.

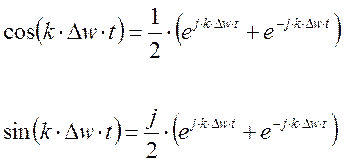
Раскрывая скобки и собирая коэффициенты при и  получаем:

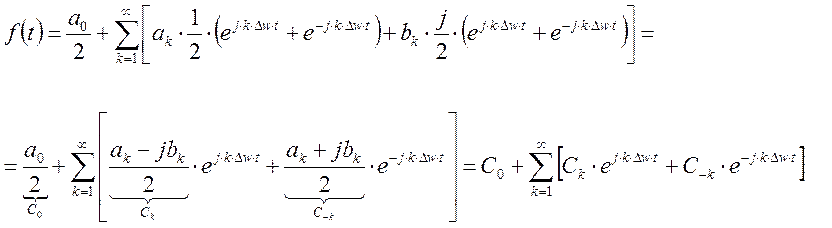
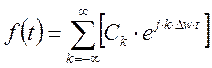 - комплексная форма ряда Фурье.

 - комплексные коэффициенты разложения периодической функции  в ряд Фурье.

 - комплексная гармоника.

Определим :

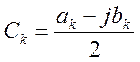, где

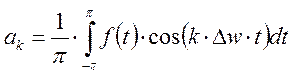
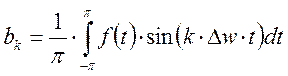
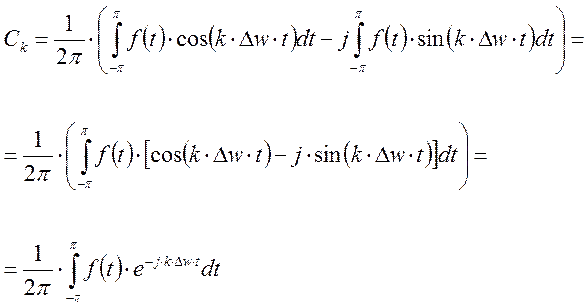
Вопросы для самоконтроля.

1.  В каком случае функции являются ортогональными.

2.  Как происходит гармонический синтез функции с периодом 2π.

3.  Какими выражениями определяются коэффициенты ряда Фурье.

4.  Расскажите о частных случаях ряда Фурье.

5.  Вывести формулы для определения коэффициентов ряда Фурье на промежутке от  0 до π.

6.  Вывести формулы для определения коэффициентов ряда Фурье на промежутке от  0 до l.

7.  Вывести формулы для определения коэффициентов ряда Фурье на промежутке от  -l до l.

8.  Как перейти к комплексной форме ряда Фурье.

ЛЕКЦИЯ 2

ИНТЕГРАЛ ФУРЬЕ.

Цель. Изучить понятие интеграла Фурье.

Задачи.

1.Изучить интеграл Фурье для функции с периодом 2π.

2. рассмотреть частные случаи интеграла Фурье.

3. Изучить комплексную форму интеграла Фурье.

Допустим функция  периодическая и рассмотрим ее на промежутке 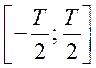. При представлении функции   в виде ряда Фурье на промежутке 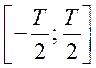, функция периодически продолжается с периодом  за пределы интервала. В этом случае получающаяся периодическая функция представляется в виде бесконечной суммы гармоник. Установим, как будет изменяться разложение функции на сумму гармоник, если  Функция  - имеет разложение в ряд Фурье вида:

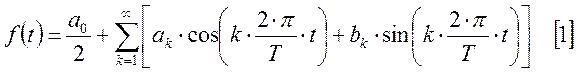
Коэффициенты для непериодической функции для этого промежутка:

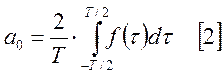
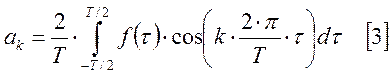
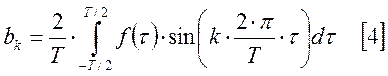
Предположим, что  на всей оси t удовлетворяет условию абсолютной интегрируемости:

,

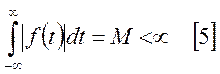то есть [5] существует.

Подставим [2]-[4] в [1].

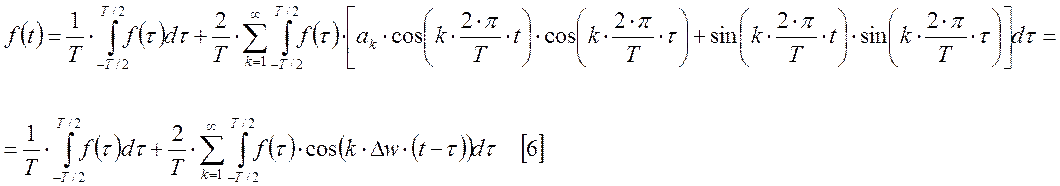
Оценим модуль первого слагаемого ().

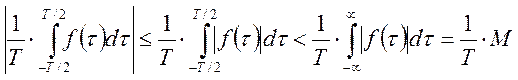
при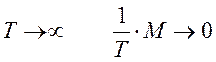

Оценим второе слагаемое при . Частота первой гармоники 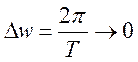. Однако величина  является приращением частоты при переходе к совокупности частот гармоники  от одной частоты к соседней. При . приращение частот есть величина очень маленькая и в этом случае приращение частоты  можно отождествить с дифференциалом. В этом случае [6] представляет собой:

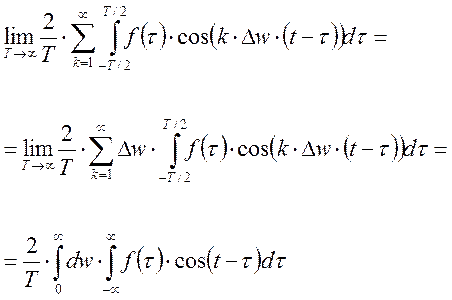
Для непериодической функции:

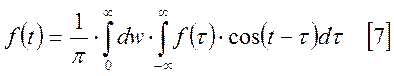 - интеграл Фурье.

В полученном выражении распишем косинус разности для нахождения коэффициентов Фурье.

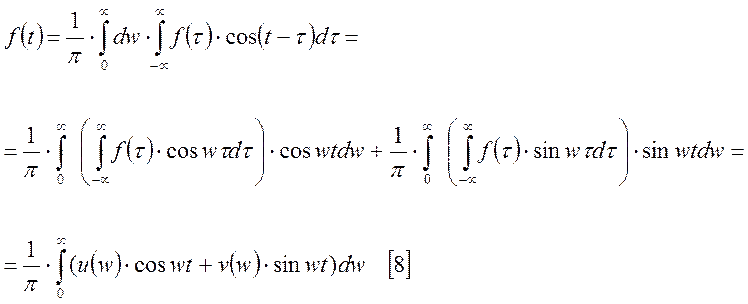
Коэффициенты  являются коэффициентами интеграла Фурье и соответственно коэффициентами .

Частный случай интеграла Фурье.

Рассмотри частный случай разложения интеграла Фурье.

 - четная:

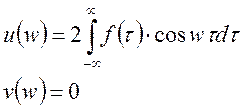
Если  - четная, то интеграл Фурье примет вид:

.

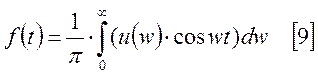 - нечетная:

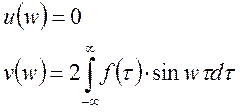
Если  - нечетная, то интеграл Фурье примет вид:

.

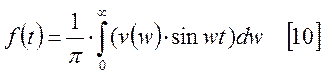Формулы [8] и ее частные случаи [9], [10] характеризуют разложение непериодической функции  на сумму гармонических составляющих с частотами w и непрерывно изменяющихся на интервале .

Комплексная форма интеграла Фурье.

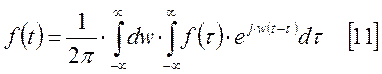
Допустим [11] имеет смысл.

Полученное выражение подставим в [11].

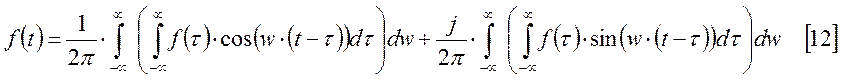
Выражения в круглых скобках в 1 и во 2 слагаемом являются соответственно четной и нечетной функцией относительно w, поэтому.

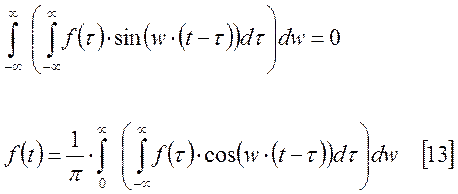
Сравнивая [13] с выражением для интеграла Фурье [7], приходим к выводу, что они идентичны. Следовательно [11] является комплексной формой интеграла Фурье. В [11] множитель  не зависит от следовательно можно его вынести из под знака интеграла. Тогда получим:

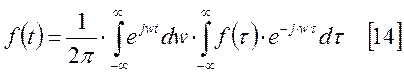
Перейдем от  к .

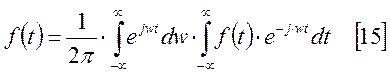
Формула 15 имеет своим аналогом комплексную форму ряда Фурье, и здесь роль коэффициента  играет внутренний интеграл Обозначим его как:

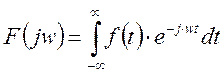
Тогда [15] примет вид:

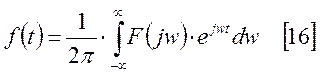
Функция  является спектральной плотностью функции .

Вопросы для самоконтроля.

1.  какой вид имеет разложение для интеграла Фурье.

2.  Какую аналогию можно провести для интеграла с рядом Фурье.

3.  Если функция четная, как выглядит для нее интеграл Фурье.

4.   Если функция нечетная, как выглядит для нее интеграл Фурье.

5.  Какой вид имеет комплексная форма  интеграла Фурье.

ЛЕКЦИЯ 3

СПЕКТРАЛЬНЫЙ АНАЛИЗ И СИНТЕЗ ФУНКЦИИ.

Цель. Изучить спектральный состав сигналов.

Задачи:

1.  Изучить типы и свойства  спектров.

2.  Изучить частотные спектры  функций.

3.  Изучить спектры некоторых типовых сигналов.

4.  Изучить понятие спектральной характеристики.

Рассмотрим непрерывные и дискретные спектры.

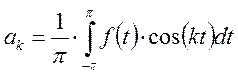
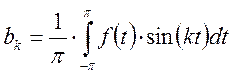
Совокупность коэффициентов  и  при разложении периодической функции в ряд Фурье называются частотными спектрами этой функции.

 и  являются зависимыми от номера гармоники k.

Графически частотные спектры изображаются в виде отрезков длины  и  перпендикулярно оси на которой откладываются значения либо  , либо .

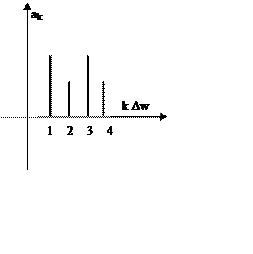
Расстояние между отдельными отрезками равно 1, если , и , если период равен .

Совокупность коэффициентов   при комплексном разложении ряда Фурье называется комплексным спектром периодической функции.

Совокупности  и  называются амплитудными и фазовыми частотными спектрами периодической функции .

Спектры  тоже изображаются в виде отдельных отрезков. При комплексной форме коэффициенты могут быть положительными и отрицательными. В этом случае.

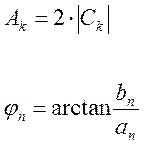
Рассмотрим .

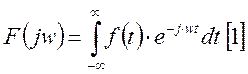Данное выражение называется спектральной плотностью или спектральной характеристикой периодической функции . Сравним [1] с выражением для комплексной амплитуды -ой гармоники ряда Фурье.

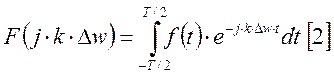
Если . Тогда правые части выражений [1] и [2] совпадают. При этом получим:

 

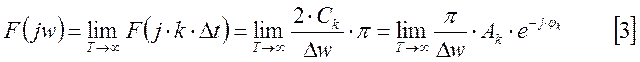
Для  при различных  принимает дискретный ряд значений относительно комплексной амплитуды -ой гармоники при разложении периодической функции. Функция  характеризует закон изменения относительной комплексной амплитуды разложение непериодических функций на сумму гармоник, так как частота  при разложении непериодических функций принимает непрерывный ряд значений, то график функции  будет непрерывной кривой.

При разложении непериодической функции в случае, когда  разложение будет представлять из себя сумму бесконечного числа гармоник, частота которых будет отличаться друг от друга на бесконечно малую величину. При построении графика амплитудно-частотного спектра непериодических процессов по оси ординат откладывается не амплитуда гармоники А, а относительна амплитуда: