Физика \ Физика

Система оценки уровня эффективности ЗАО «Тяжпромарматура», страница 8

Для нахождения естественного нуля функции «средняя валовая прибыль» с левой стороны возьмём точку x0, что не вошло в уровневое множество А0,04, и сравним его с x10. На основании мнения экспертов, получаем, что () <().  Отсюда получаем, что точка x0 не входит в уровневое множество А0,04 и она является точкой естественного нуля.

Для нахождения естественного нуля функции «средняя валовая прибыль» с правой стороны возьмём точку x110, что не вошло в уровневое множество А0,04, и сравним его с x100. На основании мнения экспертов, получаем, что () >() и () =(). Отсюда получаем, что x110 является точкой естественного нуля.

Для нахождения естественного максимума функции «средняя валовая прибыль»  с левой стороны возьмём точку x40, а  c правой x60, что не вошли в уровневое множество А1, и сравним их с x50. На основании мнения экспертов, получаем, что () < () и () >(), а также, что ()=()…=() и () =()…=().Отсюда получаем, что точки x40 и x60 не входят в уровневое множество А1 и точка x50 является точкой максимума.

D - Маржинальная прибыль

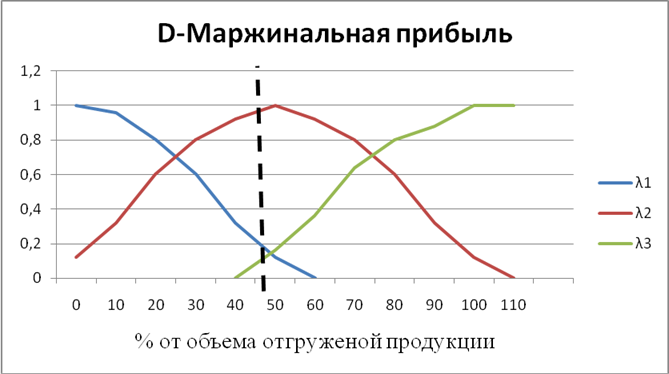
λ1 – низкая маржинальная прибыль         

A0,04={x0,x10,x20,x30,x40,x50}

A0,08={x0,x10,x20,x30,x40,x50}

A0,12={x0,x10,x20,x30,x40,x50}

T50

T40

T30

T20 = 4,92

T104,92= 6,92

T0
 
A0,16={x0,x10,x20,x30,x40}

A0,2={x0,x10,x20,x30,x40}

A0,24={x0,x10,x20,x30,x40}

A0,28={x0,x10,x20,x30,x40}

A0,32={x0,x10,x20,x30,x40}

A0,36={x0,x10,x20,x30}

A0,4={x0,x10,x20,x30}

A0,44={x0,x10,x20,x30}

P50=0,02

P40=0,06

P30=0,13

P20=0,1968

P10=0,2768

P0=0,3168
 
A0,48={x0,x10,x20,x30}

A0,52={x0,x10,x20,x30}

A0,56={x0,x10,x20,x30}

A0,6={x0,x10,x20,x30}

A0,64={x0,x10,x20}

A0,68={x0,x10,x20}

m50=0,12

m40=0,32

m30=0,6

m20=0,8

m10=0,96

m0=1
 
A0,72={x0,x10,x20}

A0,76={x0,x10,x20}

A0,8={x0,x10,x20}

A0,84={x0,x10}

A0,88={x0,x10}

A0,92={x0,x10}

A0,96={x0, x10}

A1={x0}

Для нахождения естественного нуля функции «низкая маржинальная прибыль» возьмём x60, что не вошло в уровневое множество А0,04, и сравним его с x50.

На основании мнения экспертов, получаем, что () >(), но () >(), тогда x60 не входит в множество А0,04, но и не является естественным нулем. Тогда () =()=…=(). Естественный ноль – точа x70.

Для нахождения естественного максимума функции «низкая маржинальная прибыль»  возьмём точку x10, что не вошло в уровневое множество А1, и сравним его с x0. На основании мнения экспертов, получаем, что () >(). Отсюда получаем, что точка x10 не входит в уровневое множество А1 и x0 является точкой максимума.

λ3 – высокая маржинальная прибыль

T50

T60

T70

T80

T90

T100
 
A0,04={x50, x60,x70,x80,x90,x100}

A0,08={x50, x60,x70,x80,x90,x100}

A0,12={x50, x60,x70,x80,x90,x100}

A0,16={x50,x60,x70,x80,x90,x100}

A0,2={x60,x70,x80,x90,x100}

A0,24={x60,x70,x80,x90,x100}

A0,28={x60,x70,x80,x90,x100}

A0,32={x60,x70,x80,x90,x100}

P50=0,0268

P60=0,0668

P70=0,1368

P80=0,19

P90=0,23

P100=0,35
 
A0,36={x60,x70,x80,x90,x100}

A0,4={x70,x80,x90,x100}

A0,44={x70,x80,x90,x100}

A0,48={x70,x80,x90,x100}

A0,52={x70,x80,x90,x100}

A0,56={x70,x80,x90,x100}

A0,6={x70,x80,x90,x100}

m50=0,1608

m60=0,36

m70=0,64

m80=0,8

m90=0,88

m100=1
 
A0,64={x70,x80,x90,x100}

A0,68={x80,x90,x100}

A0,72={x80,x90,x100}

A0,76={x80,x90,x100}

A0,8={x80,x90,x100}

A0,84={x90,x100}

A0,88={x90,x100}

A0,92={x100}

A0,96={x100}

A1={x100}

Для нахождения естественного нуля функции «высокая маржинальная прибыль» возьмём x50, что не вошло в уровневое множество А0,04, и сравним его с x60.

Скачать файл