Система оценки уровня эффективности ЗАО «Тяжпромарматура», страница 3

Если А, В,…,С - набор лингвистических переменных, описывающих ситуацию принятия решения, (a₁,…, a_р), (b₁,…, b_q),…,(g₁,…,g_r) - наборы соответствующих нечетких переменных, X,Y,...,Z - шкалы, в которых измеряются значения признаков, соответствующих лингвистическим переменным, то каждому набору (a_i, b_j,…, g_k) соответствует управленческое решение ω₁, составляют эталонный класс L₁, так же определяются классы L₂,...,L_m.

5 этап. На заключительном этапе строится расплывчатая классификационная модель (U,P,W). Расплывчатый эталонный класс P_l, l=1,...,m, характеризуется функцией принадлежности.

m(x₀,y₀,...,z₀) =  Vm_ai(x₀) Ùm_bi(y₀)Ù...Ù m_gk(z₀).

^{(ai, bi,..., gk)Î L1}

Выбирается управленческое решение ω_1, для которого функция принадлежности максимальна,

m_р1(x₀,y₀,...,z₀) = max{m_р1(x₀,y₀,...,z₀),..., m_рm(x₀,y₀,...,z₀)}

1.4.  Порядок вычисления функции принадлежности на основе использования уровневых множеств и формулы полной вероятности

1 этап. Определяем объем выборки M необходимый для построения функции принадлежности.

2 этап. Выбираем число уровней N, на которое делится промежуток от 0 до 1.

3 этап. Единичный интервал  делится на n частей равной длины S.

4 этап. Случайным образом выбирается элемент а из S.

5 этап. Эксперт выбирает все элементы , которые принадлежат множеству уровня Аа.

6 этап. Если k-число элементов, включенных в множество уровня, то при каждом появлении этого элемента к  прибавляется .

 – число элементов, включённых во множество уровня;

 – число уровней.

7 этап. Повторяем этапы 4-6 до тех пор пока не будут выбраны все уровни, перечисленные в множестве S.

8 этап. Подсчитываем вероятность:

9 этап. Полученные оценки вероятностей упорядочиваем по возрастанию и подставляем в формулу  для расчета степени принадлежности  элемента .

2.  Практическая часть.

Применим метод расплывчатой классификационной модели  для оценки эффективности предприятия ЗАО «арматура».

2.1.  Выделение показателей

Выделение  четырех показателей и их лингвистические переменные: фактический выпуск готовой продукции, полная производственная себестоимость отгруженной продукции, валовая прибыль, маржинальная прибыль. Каждому показателю соответствуют нечеткие переменные (их значения):

V: А - Фактический выпуск готовой продукции

X: B - Полная производственная себестоимость

Y: C - Валовая прибыль

Z: D - Маржинальная прибыль

Для лингвистической переменной «A»

α₁ – низкий

α₂ – средний

α₃ – высокий

Для лингвистической переменной «B»

β₁ – низкая

β₂ – средняя

β₃ – высокая

Для лингвистической переменной «C»

γ₁ – низкая

γ₂ – средняя

γ₃ – высокая

Для лингвистической переменной «D»

λ₁ – низкая

λ₂ – средняя

λ₃ – высокая

R – Множество управленческих решений:

r₁ – «низкая степень эффективности»

r₂ – «средняя степень эффективности (требует корректирующих действий)

r₃ – «высокая степень эффективности»

2.2.  Построение функций принадлежности для каждого показателя.

Число уровней: N = 25

Единичный интервал:

Используемые формулы:

1. 

 – число элементов, включённых во множество уровня;

 – число уровней.

2. 

3. 

А - Фактический выпуск готовой продукции

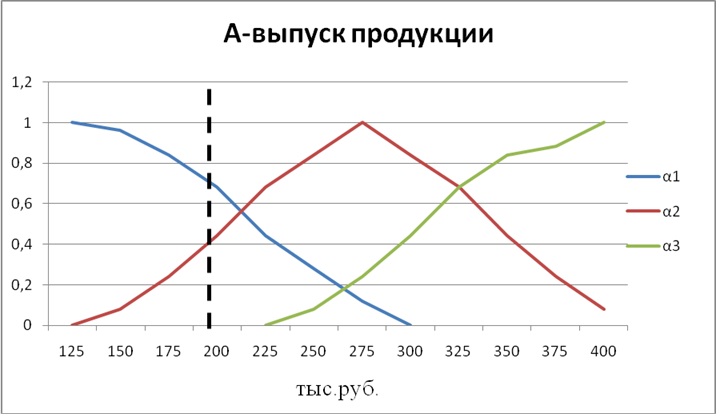
α₁ – низкий выпуск

T275 T250 T225 T200 T175 T150 T125

A_0,04={x₁₂₅,x₁₅₀,x₁₇₅,x₂₀₀,x₂₂₅,x₂₅₀,x₂₇₅}

A_0,08={x₁₂₅,x₁₅₀,x₁₇₅,x₂₀₀,x₂₂₅,x₂₅₀,x₂₇₅}

A_0,12={x₁₂₅,x₁₅₀,x₁₇₅,x₂₀₀,x₂₂₅,x₂₅₀,x₂₇₅}

A_0,16={x₁₂₅,x₁₅₀,x₁₇₅,x₂₀₀,x₂₂₅,x₂₅₀}      

A_0,2={x₁₂₅,x₁₅₀,x₁₇₅,x₂₀₀,x₂₂₅,x₂₅₀}

A_0,24={x₁₂₅,x₁₅₀,x₁₇₅,x₂₀₀,x₂₂₅,x₂₅₀}

A_0,28={x₁₂₅,x₁₅₀,x₁₇₅,x₂₀₀,x₂₂₅,x₂₅₀}

A_0,32={x₁₂₅,x₁₅₀,x₁₇₅,x₂₀₀,x₂₂₅}

A_0,36={x₁₂₅,x₁₅₀,x₁₇₅,x₂₀₀,x₂₂₅}

P275=0,01712 P250=0,0438 P225=0,0758 P200=0,1358 P175=0,18912 P150=0,24912 P125=0,28912

A_0,4={x₁₂₅,x₁₅₀,x₁₇₅,x₂₀₀,x₂₂₅}

A_0,44={x₁₂₅,x₁₅₀,x₁₇₅,x₂₀₀,x₂₂₅}

A_0,48={x₁₂₅,x₁₅₀,x₁₇₅,x₂₀₀}

A_0,52={x₁₂₅,x₁₅₀,x₁₇₅,x₂₀₀}